2.2.2用样本的数字特征估计总体的数字特征(共37张PPT)
文档属性
| 名称 | 2.2.2用样本的数字特征估计总体的数字特征(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 15:35:01 | ||
图片预览









文档简介
(共37张PPT)
1.众数、中位数、平均数的概念
2.标准差
在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发挥的更稳定些吗?
为了从整体上更好地把握总体的规律,我们要通过样本的数据对总体的数字特征进行研究。
用样本的数字特征估计总体的数字特征
众数、中位数、平均数的概念
平均数: 一组数据的算术平均数,即
x=
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
众数、中位数、平均数与频率分布直方图的关系?
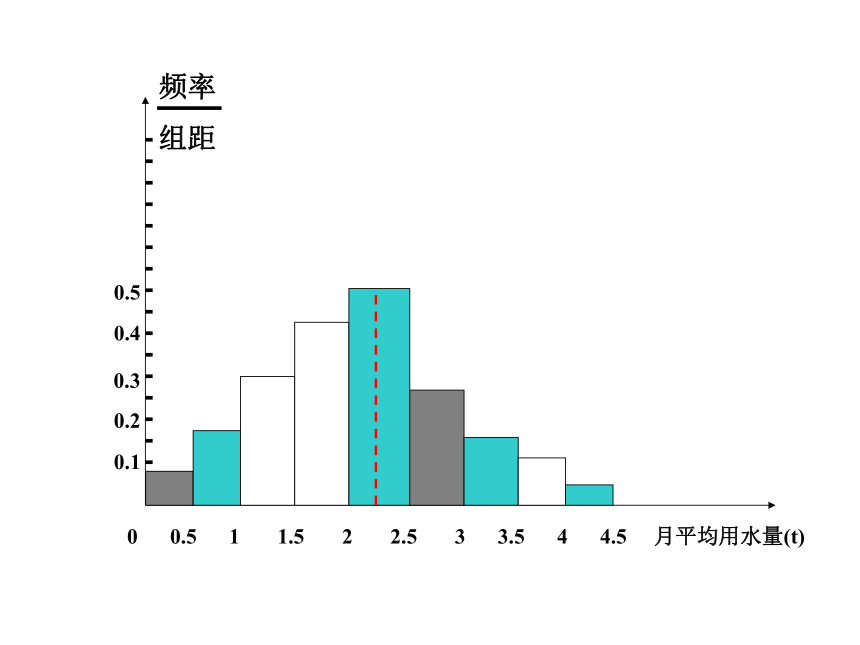
1. 众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示:
2. 在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。此数据值为2.02t,下图中虚线代表居民月均用水量的中位数的估计值。
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致。
2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中的原因吗?
3. 平均数是频率分布直方图的“重心”,是直方图的平衡点. n 个样本数据的平均数由公式:
X=
下图显示了居民月均用水量的平均数: x=1.973
比较:三种数字特征的优缺点
1. 众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少。
2. 中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。
3.由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。
某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用如图所示的条形图表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
A. 0.6h B. 0.9h C. 1.0h D. 1.5h
B
在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8,6,7,7.
如果你是教练,你应如何判断哪个运动员发挥的更稳定些吗?
如果看两人本次射击的平均成绩,由于
两人射击的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
甲的成绩比较分散,乙的成绩相对集中
分别作甲乙成绩的统计图表,如下
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
标准差
样本数据 的标准差的算法:
(1)算出样本数据的平均数
(2)算出每个样本数据与样本数据平均数的差:
(3)算出(2)中的 平方。
(4)算出(3)中n个平方数的平均数,即为样本方差。
(5)算出(4)中平均数的算术平方根,,即为样本标准差。
为了方便求的标准差,我们给出计算公式:如下
为了计算方便,在做题的时候习惯要求求方差,即S2.
显然,标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小。
标准差的取值范围是什么?标准差为0的样本数据有什么特点?
从标准差的定义和计算公式都可以得出: 当 时,意味着所有的样本数据都等于样本平均数。
画出下列四组样本数据的直方图,说明他们的异同点。
(1)5,5,5,5,5,5,5,5,5
(2)4,4,4,5,5,5,6,6,6
(3)3,3,4,4,5,6,6,7,7
(4)2,2,2,2,5,8,8,8,8
解:四组样本数据的直方图是:
(
四组数据的平均数都是5.0,标准差分别为:0,0.82,1.49,2.83。
他们有相同的平均数,但他们有不同的标准差,说明数据的分散程度是不一样的。
1.众数、中位数、平均数的概念
平均数: 一组数据的算术平均数,即
x=
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
2. 标准差的概念
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
3. 标准差的计算公式
1.(2019上海)在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7天”,根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4
B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3
D.丁地:总体均值为2,总体方差为3
D
解析:
甲地取0,0,0,0,4,4,4,4,4,10,该组数据均值为3,中位数为4显然不符合该标志;
乙地取0,0,0,0,0,0,0,0,0,10,该组数据中位数为2,众数为3,显然也不符合该标志;
丙地取0,0,1,1,2,2,3,3,3,10,该组数据中位数为2,众数为3,显然也不符合该标致;
丁地的均值为2,则样本总和为20,由于总体方差为3,可知改组每一个数据与2的差的平方和为30,若该组数据中有一个超过7,则其方差必大于3,于是可得丁地一定符合该标志,故选D。
2.(2019江苏)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
则以上两组数据的方差中较小的一个为s2=____
学生 1号 2号 3号 4号 5号
甲班 6 7 7 8 7
乙班 6 7 6 7 9
解析:
本题考查了统计初步中样本数据的求解问题,属简单的公式应用问题,由图表可得。
s2甲<s2乙
两组数据的方差中较小的一个为s2= 。
120
解析:
1在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为____________;
9.5,0.016
在数据统计中,能反映一组数据变化范围大小的指标是( )
A.极差 B.方差 C.标准差 D.以上都不对
4. 已知一个样本:1,3,2,5,x,若它的平均数是3,则这个样本的标准差是____
A
5. 若样本x1,x2…xn的方差是0,则表示( )
X=0 B.x1=x2…=xn
C. x1=x2…=xn=0 D.总体方差一定等于0
B
1.众数、中位数、平均数的概念
2.标准差
在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发挥的更稳定些吗?
为了从整体上更好地把握总体的规律,我们要通过样本的数据对总体的数字特征进行研究。
用样本的数字特征估计总体的数字特征
众数、中位数、平均数的概念
平均数: 一组数据的算术平均数,即
x=
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
众数、中位数、平均数与频率分布直方图的关系?
1. 众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示:
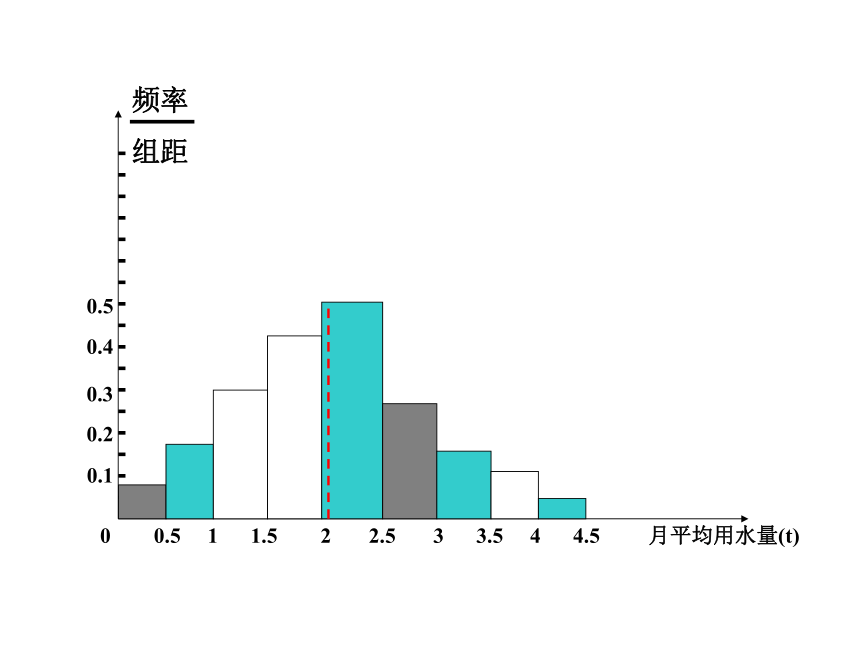
2. 在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。此数据值为2.02t,下图中虚线代表居民月均用水量的中位数的估计值。
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致。
2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中的原因吗?
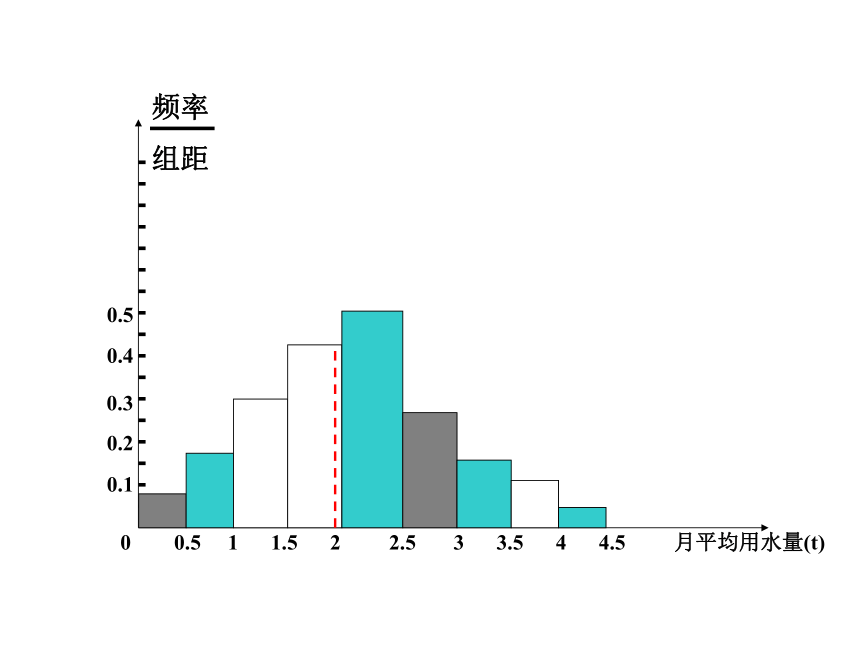
3. 平均数是频率分布直方图的“重心”,是直方图的平衡点. n 个样本数据的平均数由公式:
X=
下图显示了居民月均用水量的平均数: x=1.973
比较:三种数字特征的优缺点
1. 众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少。
2. 中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。
3.由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。
某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用如图所示的条形图表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
A. 0.6h B. 0.9h C. 1.0h D. 1.5h
B
在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8,6,7,7.
如果你是教练,你应如何判断哪个运动员发挥的更稳定些吗?
如果看两人本次射击的平均成绩,由于
两人射击的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
甲的成绩比较分散,乙的成绩相对集中
分别作甲乙成绩的统计图表,如下
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
标准差
样本数据 的标准差的算法:
(1)算出样本数据的平均数
(2)算出每个样本数据与样本数据平均数的差:
(3)算出(2)中的 平方。
(4)算出(3)中n个平方数的平均数,即为样本方差。
(5)算出(4)中平均数的算术平方根,,即为样本标准差。
为了方便求的标准差,我们给出计算公式:如下
为了计算方便,在做题的时候习惯要求求方差,即S2.
显然,标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小。
标准差的取值范围是什么?标准差为0的样本数据有什么特点?
从标准差的定义和计算公式都可以得出: 当 时,意味着所有的样本数据都等于样本平均数。
画出下列四组样本数据的直方图,说明他们的异同点。
(1)5,5,5,5,5,5,5,5,5
(2)4,4,4,5,5,5,6,6,6
(3)3,3,4,4,5,6,6,7,7
(4)2,2,2,2,5,8,8,8,8
解:四组样本数据的直方图是:
(
四组数据的平均数都是5.0,标准差分别为:0,0.82,1.49,2.83。
他们有相同的平均数,但他们有不同的标准差,说明数据的分散程度是不一样的。
1.众数、中位数、平均数的概念
平均数: 一组数据的算术平均数,即
x=
中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
2. 标准差的概念
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
3. 标准差的计算公式
1.(2019上海)在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7天”,根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4
B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3
D.丁地:总体均值为2,总体方差为3
D
解析:
甲地取0,0,0,0,4,4,4,4,4,10,该组数据均值为3,中位数为4显然不符合该标志;
乙地取0,0,0,0,0,0,0,0,0,10,该组数据中位数为2,众数为3,显然也不符合该标志;
丙地取0,0,1,1,2,2,3,3,3,10,该组数据中位数为2,众数为3,显然也不符合该标致;
丁地的均值为2,则样本总和为20,由于总体方差为3,可知改组每一个数据与2的差的平方和为30,若该组数据中有一个超过7,则其方差必大于3,于是可得丁地一定符合该标志,故选D。
2.(2019江苏)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
则以上两组数据的方差中较小的一个为s2=____
学生 1号 2号 3号 4号 5号
甲班 6 7 7 8 7
乙班 6 7 6 7 9
解析:
本题考查了统计初步中样本数据的求解问题,属简单的公式应用问题,由图表可得。
s2甲<s2乙
两组数据的方差中较小的一个为s2= 。
120
解析:
1在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为____________;
9.5,0.016
在数据统计中,能反映一组数据变化范围大小的指标是( )
A.极差 B.方差 C.标准差 D.以上都不对
4. 已知一个样本:1,3,2,5,x,若它的平均数是3,则这个样本的标准差是____
A
5. 若样本x1,x2…xn的方差是0,则表示( )
X=0 B.x1=x2…=xn
C. x1=x2…=xn=0 D.总体方差一定等于0
B
