磁聚焦(一)PDF版含答案
文档属性
| 名称 | 磁聚焦(一)PDF版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 229.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-31 00:00:00 | ||
图片预览

文档简介
第 1页,总 3页
磁聚焦(培优一)
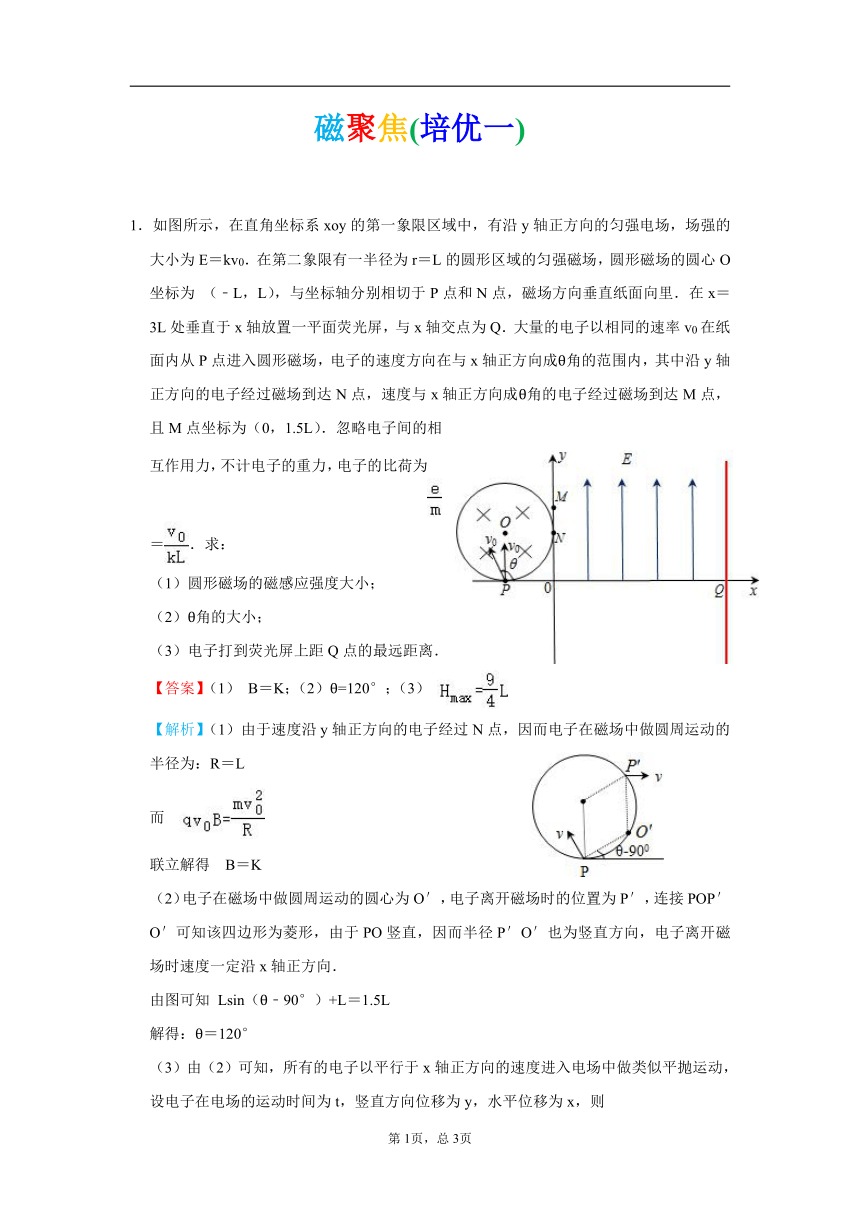
1.如图所示,在直角坐标系 xoy的第一象限区域中,有沿 y轴正方向的匀强电场,场强的
大小为 E=kv0.在第二象限有一半径为 r=L的圆形区域的匀强磁场,圆形磁场的圆心 O
坐标为 (﹣L,L),与坐标轴分别相切于 P点和 N点,磁场方向垂直纸面向里.在 x=
3L处垂直于 x轴放置一平面荧光屏,与 x轴交点为 Q.大量的电子以相同的速率 v0在纸
面内从 P点进入圆形磁场,电子的速度方向在与 x轴正方向成θ角的范围内,其中沿 y轴
正方向的电子经过磁场到达 N点,速度与 x轴正方向成θ角的电子经过磁场到达 M点,
且M点坐标为(0,1.5L).忽略电子间的相
互作用力,不计电子的重力,电子的比荷为
= .求:
(1)圆形磁场的磁感应强度大小;
(2)θ角的大小;
(3)电子打到荧光屏上距 Q点的最远距离.
【答案】(1) B=K;(2)θ=120°;(3)
【解析】(1)由于速度沿 y轴正方向的电子经过 N点,因而电子在磁场中做圆周运动的
半径为:R=L
而
联立解得 B=K
(2)电子在磁场中做圆周运动的圆心为 O′,电子离开磁场时的位置为 P′,连接 POP′
O′可知该四边形为菱形,由于 PO竖直,因而半径 P′O′也为竖直方向,电子离开磁
场时速度一定沿 x轴正方向.
由图可知 Lsin(θ﹣90°)+L=1.5L
解得:θ=120°
(3)由(2)可知,所有的电子以平行于 x轴正方向的速度进入电场中做类似平抛运动,
设电子在电场的运动时间为 t,竖直方向位移为 y,水平位移为 x,则
第 2页,总 3页
水平方向:x=v0t
竖直方向:
eE=ma
vy=at
联立解得:x=
设电子最终打在光屏的最远点距 Q点为 H,电子射出电场时的夹角为θ,有:
有:H=(3L﹣x)tanθ=
当 时,即 时,H有最大值.
由于 L 所以
2.如图 1所示,在 x﹣o﹣z平面内有一半径为 a的圆形匀强磁场区域,磁场垂直 x﹣o﹣z
平面,该区域与 x轴、z轴相切.z轴上有一线状发射源在 z=a 至 z=2a段沿+x方向发
射速度均为 v的质子(质子的质量为 m,电量为+q),此圆形磁场区域的磁感应强度 B=
,不计质子间的作用,则
(1)试求该群质子在磁场 B中运动的轨道半径 r;
(2)为使射入该圆形磁场区域的质子平行射出磁场,需将圆形磁场阴影部分(半圆)内
的部分区域的磁场去除,试分析磁场的方向,并求出去除的磁场区域最小面积;
(3)若在 z<0区域中存在沿 x轴正方向的磁场,磁感应强度在空间按 B′=B0x变化,
则从第(2)问中平行射出的质子经过 x轴后进入 B′磁场,然后经过 x﹣o﹣y平面,试
分析各质子经过 x﹣o﹣y平面的位置的坐标 x、y之间的函数关系.
第 3页,总 3页
【答案】(1)r=a;(2)S= ;(3)y= (a≤x≤2a).
【解析】(1)质子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m ,解得:r=a;
(2)质子经过磁场后平行磁场射出,质子在磁
场中速度偏角为 90°,
去除部分磁场边界为圆弧,如图所示:
S 扇形= πa2,S 三角形= a2,
S=2(S 扇形﹣S 三角形)= ;
(3)粒子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB′=m ,
由几何知识得:y=2r,
由题意可知:B′=B0x,
解得:y= (a≤x≤2a);
磁聚焦(培优一)
1.如图所示,在直角坐标系 xoy的第一象限区域中,有沿 y轴正方向的匀强电场,场强的
大小为 E=kv0.在第二象限有一半径为 r=L的圆形区域的匀强磁场,圆形磁场的圆心 O
坐标为 (﹣L,L),与坐标轴分别相切于 P点和 N点,磁场方向垂直纸面向里.在 x=
3L处垂直于 x轴放置一平面荧光屏,与 x轴交点为 Q.大量的电子以相同的速率 v0在纸
面内从 P点进入圆形磁场,电子的速度方向在与 x轴正方向成θ角的范围内,其中沿 y轴
正方向的电子经过磁场到达 N点,速度与 x轴正方向成θ角的电子经过磁场到达 M点,
且M点坐标为(0,1.5L).忽略电子间的相
互作用力,不计电子的重力,电子的比荷为
= .求:
(1)圆形磁场的磁感应强度大小;
(2)θ角的大小;
(3)电子打到荧光屏上距 Q点的最远距离.
【答案】(1) B=K;(2)θ=120°;(3)
【解析】(1)由于速度沿 y轴正方向的电子经过 N点,因而电子在磁场中做圆周运动的
半径为:R=L
而
联立解得 B=K
(2)电子在磁场中做圆周运动的圆心为 O′,电子离开磁场时的位置为 P′,连接 POP′
O′可知该四边形为菱形,由于 PO竖直,因而半径 P′O′也为竖直方向,电子离开磁
场时速度一定沿 x轴正方向.
由图可知 Lsin(θ﹣90°)+L=1.5L
解得:θ=120°
(3)由(2)可知,所有的电子以平行于 x轴正方向的速度进入电场中做类似平抛运动,
设电子在电场的运动时间为 t,竖直方向位移为 y,水平位移为 x,则
第 2页,总 3页
水平方向:x=v0t
竖直方向:
eE=ma
vy=at
联立解得:x=
设电子最终打在光屏的最远点距 Q点为 H,电子射出电场时的夹角为θ,有:
有:H=(3L﹣x)tanθ=
当 时,即 时,H有最大值.
由于 L 所以
2.如图 1所示,在 x﹣o﹣z平面内有一半径为 a的圆形匀强磁场区域,磁场垂直 x﹣o﹣z
平面,该区域与 x轴、z轴相切.z轴上有一线状发射源在 z=a 至 z=2a段沿+x方向发
射速度均为 v的质子(质子的质量为 m,电量为+q),此圆形磁场区域的磁感应强度 B=
,不计质子间的作用,则
(1)试求该群质子在磁场 B中运动的轨道半径 r;
(2)为使射入该圆形磁场区域的质子平行射出磁场,需将圆形磁场阴影部分(半圆)内
的部分区域的磁场去除,试分析磁场的方向,并求出去除的磁场区域最小面积;
(3)若在 z<0区域中存在沿 x轴正方向的磁场,磁感应强度在空间按 B′=B0x变化,
则从第(2)问中平行射出的质子经过 x轴后进入 B′磁场,然后经过 x﹣o﹣y平面,试
分析各质子经过 x﹣o﹣y平面的位置的坐标 x、y之间的函数关系.
第 3页,总 3页
【答案】(1)r=a;(2)S= ;(3)y= (a≤x≤2a).
【解析】(1)质子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m ,解得:r=a;
(2)质子经过磁场后平行磁场射出,质子在磁
场中速度偏角为 90°,
去除部分磁场边界为圆弧,如图所示:
S 扇形= πa2,S 三角形= a2,
S=2(S 扇形﹣S 三角形)= ;
(3)粒子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB′=m ,
由几何知识得:y=2r,
由题意可知:B′=B0x,
解得:y= (a≤x≤2a);
同课章节目录
