五年级下册数学试题-第三单元测试卷 冀教版(含答案)
文档属性
| 名称 | 五年级下册数学试题-第三单元测试卷 冀教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 56.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 20:26:55 | ||
图片预览

文档简介
一、想一想,填一填(30分)
1.长方体是由( )或正方形(特殊情况下有两个相对面是正方形)围成的立体图形,正方体是由6个( )围成的立体图形。
2.长方体和正方体都有( )个面,( )个顶点,( )条棱。
3.相交于一个顶点的三条棱的长度分别叫做长方体的( )、( )、( )。
4.长方体(或正方体)6个面的总面积叫做它的( )。
5.一个正方体魔方的表面积是54 cm2,它的一个面的面积是( )cm2。
6.一个长方体木箱,长是60 cm,宽是50 cm,高是40 cm,则这个木箱的占地面积最大是( )cm2,表面积是( )cm2。
7.一个正方体的棱长是2 cm,把它的棱长扩大到原来的3倍,现在正方体的表面积是( )cm2。
8.焊接一个长10 cm、宽8 cm、高6 cm的长方体框架,要准备10 cm,8 cm,6 cm的铁丝各( )根。
9.一个正方体纸盒的棱长是7 cm,这个纸盒的棱长总和是( )cm。
二、我是聪明的小法官(16分)
1.有6个面、12条棱、8个顶点的立体图形一定是长方体。 ( )
2.一个棱长总和是60 cm的长方体,长、宽、高的和是15 cm。 ( )
3.正方体相邻的两个面的面积相等。 ( )
4.长方体中可以有两个面是正方形。 ( )
5.当两个相同的正方体或长方体拼在一起时,它们减少了4个面。( )
6.正方体的棱长是2厘米,它的底面积是4厘米。 ( )
7.当棱长一定时,正方体的表面积是确定的。 ( )
8.如果一个长方体的长和一个正方体的棱长相等,那么它们的表面积也相等。( )
三、看一看,选一选(10分)
1.如右图所示,A面和B面相交的边叫做长方体的( )。
A.棱 B.顶点 C.面
2.一个长方体有四个面完全相同,其他两个面是( )。
A.长方形 B.正方形 C.无法确定
3.用棱长为1 cm的小正方体拼成一个稍大的正方体,至少需用小正方体( )。
A.4个 B.8个 C.16个
4.正方体的棱长扩大到原来的8倍,它的表面积扩大到原来的( )倍。
A.8 B.16 C.32 D.64
5.把一个棱长为a的正方体任意截成两个长方体,这两个长方体表面积的和是( )。
A.6a2 B.8a2 C.2a2 D.12a2
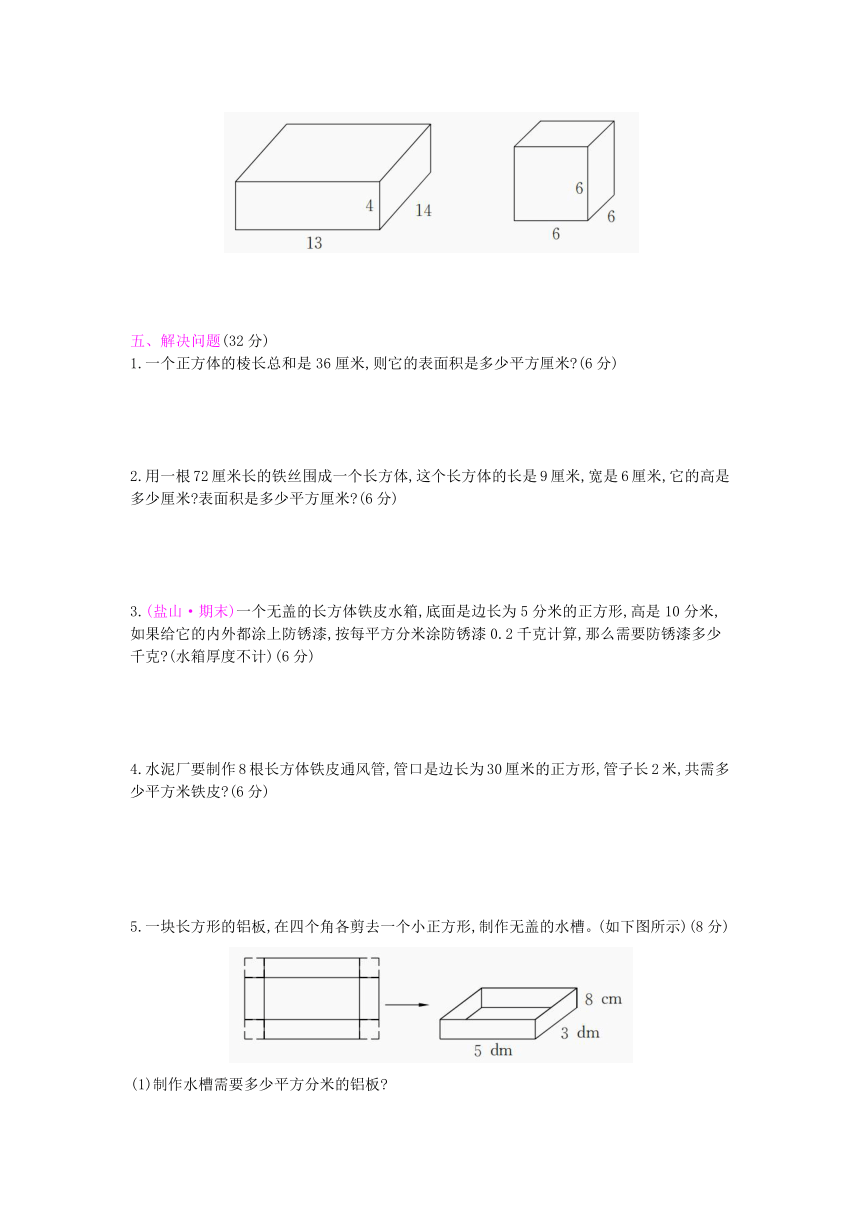
四、计算下列图形的表面积(单位:cm)(12分)
五、解决问题(32分)
1.一个正方体的棱长总和是36厘米,则它的表面积是多少平方厘米?(6分)
2.用一根72厘米长的铁丝围成一个长方体,这个长方体的长是9厘米,宽是6厘米,它的高是多少厘米?表面积是多少平方厘米?(6分)
3.(盐山·期末)一个无盖的长方体铁皮水箱,底面是边长为5分米的正方形,高是10分米,如果给它的内外都涂上防锈漆,按每平方分米涂防锈漆0.2千克计算,那么需要防锈漆多少千克?(水箱厚度不计)(6分)
4.水泥厂要制作8根长方体铁皮通风管,管口是边长为30厘米的正方形,管子长2米,共需多少平方米铁皮?(6分)
5.一块长方形的铝板,在四个角各剪去一个小正方形,制作无盖的水槽。(如下图所示)(8分)
(1)制作水槽需要多少平方分米的铝板?
(2)原来长方形铝板的面积是多少平方分米?
★挑战题
如图所示,一个正方体和一个长方体拼成一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方厘米,原来正方体的表面积是多少平方厘米?
第3单元阶段测评
一、1.长方形 正方形 2.6 8 12 3.长 宽 高 4.表面积 5.9 6.3000 14800 7.216 8.4 9.84
二、1.? 2.√ 3.√ 4.√ 5.? 6.? 7.√
8.?
三、1.A 2.B 3.B 4.D 5.B
四、(13×4+14×4+13×14)×2=580(cm2) 6×6×6=216(cm2)
五、1.36÷12=3(厘米) 3×3×6=54(平方厘米)
2.高:72÷4-9-6=3(厘米) 表面积:(9×6+9×3+6×3)×2=198(平方厘米) 3.(5×5+5×10×4)×2×0.2=90(千克) 4.30厘米=0.3米 0.3×2×4×8=19.2(平方米) 5.(1)8 cm=0.8 dm 5×3+(5×0.8+3×0.8)×2=27.8(dm2) (2)27.8+0.8×0.8×4=30.36(dm2)
★挑战题 50÷4×6=75(平方厘米)
