北师大版八年级下册数学:第一章三角形的证明回顾与思考(2)导学案+课后巩固AB(无答案)
文档属性
| 名称 | 北师大版八年级下册数学:第一章三角形的证明回顾与思考(2)导学案+课后巩固AB(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 20:01:46 | ||
图片预览

文档简介
八年级数学(下)导学案
《1三角形的证明回顾与思考(2)》导学案
【教学目标】
1、能够综合运用垂直平分线定理和角平分线定理解决问题
2、进一步掌握综合法的证明方法,结合实例体会反证法的含义;提高学生用规范的数学语言表达论证过程的能力.
【教学重点】能够综合运用垂直平分线定理和角平分线定理解决问题
【教学难点】进一步掌握综合法的证明方法,提高学生用规范的数学语言表达论证过程的能力.
【教学方法】自主探究 合作交流 归纳应用
【教学流程】
复习旧知,引入新课:
1、线段垂直平分线定理及逆定理:
2、角平分线定理及逆定理
(二)典例剖析:
类型之一 角平分线和线段的垂直平分线
1.如图1-X-8,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.5 D.6
2.如图1-X-9所示,在△ABC中,AC=BC,∠B=70°,分别以点A,C为圆心,大于1,2AC的长为半径作弧,两弧相交于点M,N,作直线MN,分别交AC,BC于点D,E,连接AE,则∠AED的度数是________°.
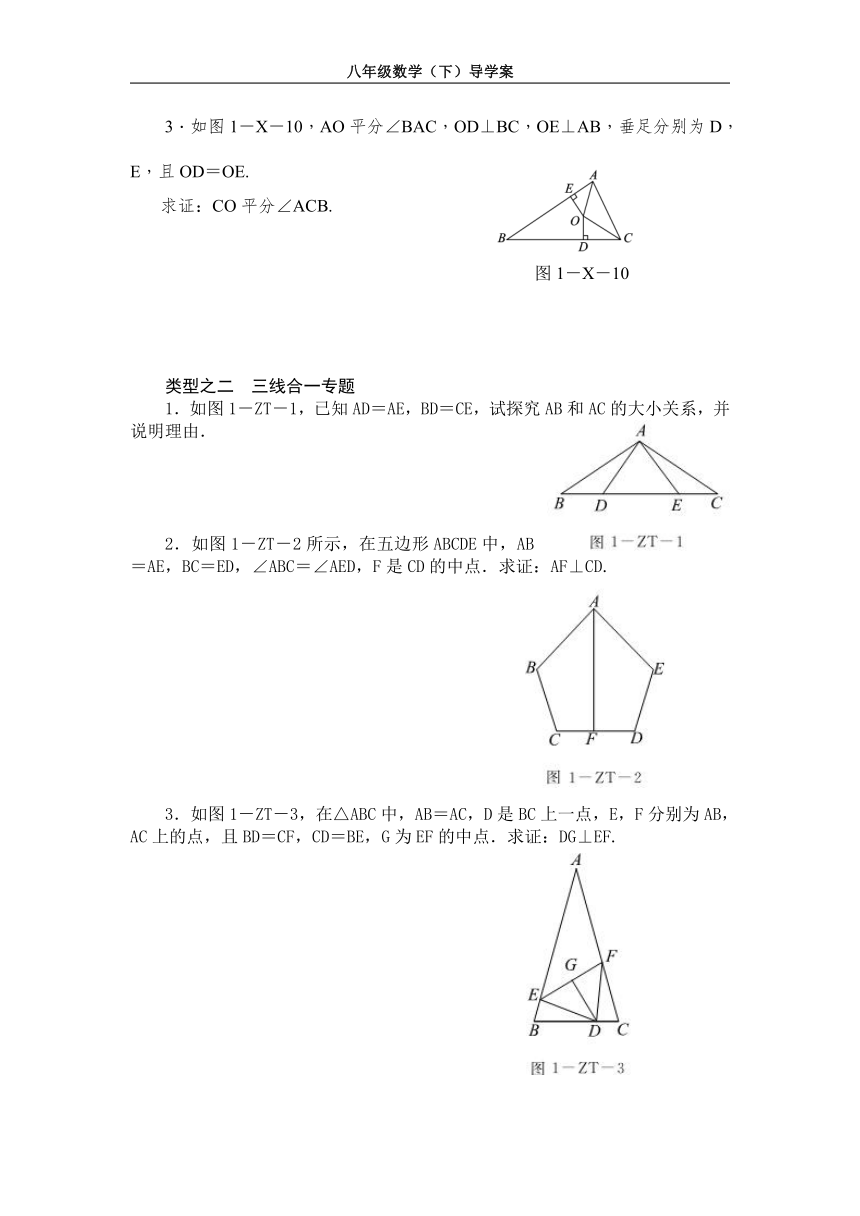
3.如图1-X-10,AO平分∠BAC,OD⊥BC,OE⊥AB,垂足分别为D,E,且OD=OE.
求证:CO平分∠ACB.
图1-X-10
类型之二 三线合一专题
1.如图1-ZT-1,已知AD=AE,BD=CE,试探究AB和AC的大小关系,并说明理由.
2.如图1-ZT-2所示,在五边形ABCDE中,AB=AE,BC=ED,∠ABC=∠AED,F是CD的中点.求证:AF⊥CD.
3.如图1-ZT-3,在△ABC中,AB=AC,D是BC上一点,E,F分别为AB,AC上的点,且BD=CF,CD=BE,G为EF的中点.求证:DG⊥EF.
类型之三 数学活动
1.如图1-X-11(a),已知点B(0,6),C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
(1)求证:BO=ED.
(2)如图(b),当点D恰好落在BC上时,
①求OC的长及点E的坐标.
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
③如图(c),M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否会发生变化?若不发生变化,请直接写出MH+MG的值;若发生变化,请简要说明理由.
(三)课堂小结:
对本节课的思想方法和学习方法归纳,
(六) 作业布置(课后巩固)分类完成A、B两类作业
【教后反思】
《1三角形的证明回顾与思考(2)》 课后巩固
班级 姓名 组别
A基础演练
1.如图,△ABC中,AB+BC=10,AC的垂直平分线分别交AB,AC于点D,E,则△BCD的周长是( )
2.如图AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF相交于点D,有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
3.如图1-Z-12所示,在△ABC中,∠CAB的平分线与BC的垂直平分线相交于点D,DM⊥AB于点M,DN⊥AC交AC的延长线于点N,你认为BM与CN之间有怎样的数量关系?请证明你的结论.
4、如图,在等边三角形ABC中,∠ABC,∠ACB的平分线相交于点O,BO,CO的垂直平分线分别交BC于点E,F,连接OE,OF,试判断△OEF的形状,并说明理由.
B.能力提升
已知P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则点P叫△ABC的费马点(Fermat point),已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,点P就是△ABC的费马点.若点P是腰长为2的等腰直角三角形DEF的费马点,则PD+PE+PF=________.
《1三角形的证明回顾与思考(2)》导学案
【教学目标】
1、能够综合运用垂直平分线定理和角平分线定理解决问题
2、进一步掌握综合法的证明方法,结合实例体会反证法的含义;提高学生用规范的数学语言表达论证过程的能力.
【教学重点】能够综合运用垂直平分线定理和角平分线定理解决问题
【教学难点】进一步掌握综合法的证明方法,提高学生用规范的数学语言表达论证过程的能力.
【教学方法】自主探究 合作交流 归纳应用
【教学流程】
复习旧知,引入新课:
1、线段垂直平分线定理及逆定理:
2、角平分线定理及逆定理
(二)典例剖析:
类型之一 角平分线和线段的垂直平分线
1.如图1-X-8,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.5 D.6
2.如图1-X-9所示,在△ABC中,AC=BC,∠B=70°,分别以点A,C为圆心,大于1,2AC的长为半径作弧,两弧相交于点M,N,作直线MN,分别交AC,BC于点D,E,连接AE,则∠AED的度数是________°.
3.如图1-X-10,AO平分∠BAC,OD⊥BC,OE⊥AB,垂足分别为D,E,且OD=OE.
求证:CO平分∠ACB.
图1-X-10
类型之二 三线合一专题
1.如图1-ZT-1,已知AD=AE,BD=CE,试探究AB和AC的大小关系,并说明理由.
2.如图1-ZT-2所示,在五边形ABCDE中,AB=AE,BC=ED,∠ABC=∠AED,F是CD的中点.求证:AF⊥CD.
3.如图1-ZT-3,在△ABC中,AB=AC,D是BC上一点,E,F分别为AB,AC上的点,且BD=CF,CD=BE,G为EF的中点.求证:DG⊥EF.
类型之三 数学活动
1.如图1-X-11(a),已知点B(0,6),C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
(1)求证:BO=ED.
(2)如图(b),当点D恰好落在BC上时,
①求OC的长及点E的坐标.
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
③如图(c),M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否会发生变化?若不发生变化,请直接写出MH+MG的值;若发生变化,请简要说明理由.
(三)课堂小结:
对本节课的思想方法和学习方法归纳,
(六) 作业布置(课后巩固)分类完成A、B两类作业
【教后反思】
《1三角形的证明回顾与思考(2)》 课后巩固
班级 姓名 组别
A基础演练
1.如图,△ABC中,AB+BC=10,AC的垂直平分线分别交AB,AC于点D,E,则△BCD的周长是( )
2.如图AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF相交于点D,有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
3.如图1-Z-12所示,在△ABC中,∠CAB的平分线与BC的垂直平分线相交于点D,DM⊥AB于点M,DN⊥AC交AC的延长线于点N,你认为BM与CN之间有怎样的数量关系?请证明你的结论.
4、如图,在等边三角形ABC中,∠ABC,∠ACB的平分线相交于点O,BO,CO的垂直平分线分别交BC于点E,F,连接OE,OF,试判断△OEF的形状,并说明理由.
B.能力提升
已知P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则点P叫△ABC的费马点(Fermat point),已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,点P就是△ABC的费马点.若点P是腰长为2的等腰直角三角形DEF的费马点,则PD+PE+PF=________.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
