北师大版八年级下册数学:第三章 图形的平移与旋转回顾与思考 导学案+课后巩固AB(无答案)
文档属性
| 名称 | 北师大版八年级下册数学:第三章 图形的平移与旋转回顾与思考 导学案+课后巩固AB(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 141.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 00:00:00 | ||
图片预览

文档简介
八年级数学(下)导学案
《第三章回顾与思考(1)》导学案
【教学目标】
1、经历构建本章知识的网络图,培养梳理知识的能力
2、灵活运用平移、旋转与中心对称的概念和性质解决相关图形问题;
【教学重点】通过例题的讲解和课堂练习对所学知识进行复习巩固;
【教学难点】章知识的综合性应用;
【教学方法】自主探究,合作交流
【教学流程】
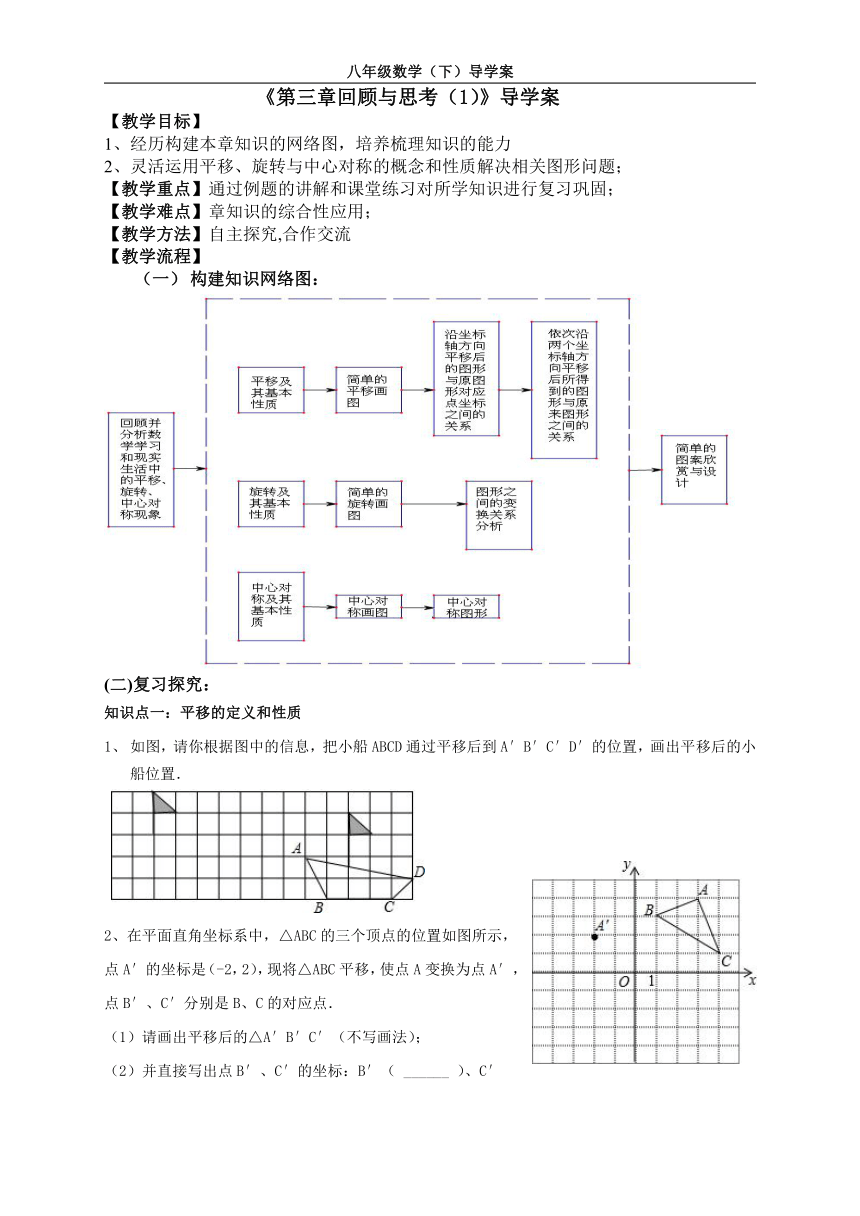
构建知识网络图:
(二)复习探究:
知识点一:平移的定义和性质
如图,请你根据图中的信息,把小船ABCD通过平移后到A′B′C′D′的位置,画出平移后的小船位置.
2、在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(-2,2),现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法);
(2)并直接写出点B′、C′的坐标:B′( ______ )、C′( ______ );
(3)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是( ______ ?).
知识点二: 旋转的定义和性质
如图,△ABC和△ADE都是等腰直角三角形.
(1)求证:BD=CE;
(2)△ABD可以看作是 ______ ,逆时针旋转 ______ °得到的.
知识点三:中心对称和中心对称图形
下列各图形都由若干个小正方形构成,其中是中心对称图形的是( )
A.?B.?C.?D.
知识点四:平移和旋转的应用
如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
如图,在Rt△ABC中,∠C=90°,M为AB边上中点,将Rt△ABC绕点M旋转,使点C与点A重合得Rt△DEA,设AE交CB于点N.
(1)若∠B=25°,求∠BAE的度数;
(2)若AC=2,BC=5,求CN的长.
【教后反思】
《第一章回顾与思考(1)》课后巩固
姓名_________ 班级_________ 组名___________
A.基础训练
1、如图所示,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,则下列结论中,错误的是??????????????( )
A.BE=EC??????????????B.BC=EF
C.AC=DF??????????????D.△ABC≌△DEF
2、以下现象:①荡秋千;②呼啦圈;③跳绳;④ 转陀螺.其中是旋转的有( )
A.①②?????B.②③???????C.③④???????D.①④
3、下列标志既是轴对称图形又是中心对称图形的是( )
4、如图所示,P是正三角形ABC内的一点,若将△PBC绕点B旋转到△P'BA,则∠PBP'的度数是?( ) A.45°??????B.60°???C.90°?????D.120°
5、已知△ABC.
(1)平移△ABC,使点A移到点A1的位置,画出平移后
得到的△A1B1C1;
(2)根据平移的性质,写出两条不同类型的正确结论.
B能力提升
6如图所示,P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转90°后能与△CBP'重合.若PB=3,求PP'得长。
《第三章回顾与思考(1)》导学案
【教学目标】
1、经历构建本章知识的网络图,培养梳理知识的能力
2、灵活运用平移、旋转与中心对称的概念和性质解决相关图形问题;
【教学重点】通过例题的讲解和课堂练习对所学知识进行复习巩固;
【教学难点】章知识的综合性应用;
【教学方法】自主探究,合作交流
【教学流程】
构建知识网络图:
(二)复习探究:
知识点一:平移的定义和性质
如图,请你根据图中的信息,把小船ABCD通过平移后到A′B′C′D′的位置,画出平移后的小船位置.
2、在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(-2,2),现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法);
(2)并直接写出点B′、C′的坐标:B′( ______ )、C′( ______ );
(3)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是( ______ ?).
知识点二: 旋转的定义和性质
如图,△ABC和△ADE都是等腰直角三角形.
(1)求证:BD=CE;
(2)△ABD可以看作是 ______ ,逆时针旋转 ______ °得到的.
知识点三:中心对称和中心对称图形
下列各图形都由若干个小正方形构成,其中是中心对称图形的是( )
A.?B.?C.?D.
知识点四:平移和旋转的应用
如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
如图,在Rt△ABC中,∠C=90°,M为AB边上中点,将Rt△ABC绕点M旋转,使点C与点A重合得Rt△DEA,设AE交CB于点N.
(1)若∠B=25°,求∠BAE的度数;
(2)若AC=2,BC=5,求CN的长.
【教后反思】
《第一章回顾与思考(1)》课后巩固
姓名_________ 班级_________ 组名___________
A.基础训练
1、如图所示,Rt△ABC沿直角边BC所在直线向右平移得到Rt△DEF,则下列结论中,错误的是??????????????( )
A.BE=EC??????????????B.BC=EF
C.AC=DF??????????????D.△ABC≌△DEF
2、以下现象:①荡秋千;②呼啦圈;③跳绳;④ 转陀螺.其中是旋转的有( )
A.①②?????B.②③???????C.③④???????D.①④
3、下列标志既是轴对称图形又是中心对称图形的是( )
4、如图所示,P是正三角形ABC内的一点,若将△PBC绕点B旋转到△P'BA,则∠PBP'的度数是?( ) A.45°??????B.60°???C.90°?????D.120°
5、已知△ABC.
(1)平移△ABC,使点A移到点A1的位置,画出平移后
得到的△A1B1C1;
(2)根据平移的性质,写出两条不同类型的正确结论.
B能力提升
6如图所示,P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转90°后能与△CBP'重合.若PB=3,求PP'得长。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
