北师大版八年级下册数学:6.4.1探索多边形的内角和与外角和(1)导学案+课后巩固AB(无答案)
文档属性
| 名称 | 北师大版八年级下册数学:6.4.1探索多边形的内角和与外角和(1)导学案+课后巩固AB(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 20:14:10 | ||
图片预览


文档简介
八年级数学(下)导学案
《6.4探索多边形的内角和与外角和(1)》导学案
【教学目标】1.了解多边形及正多边形的定义;
2. 探索多边形的内角和公式及外角和;
【教学重点】多边形内角和与外角和定理的探索和应用
【教学难点】多边形定义的理解;多边形内角和与外角和公式的推导;转化的数学思维方法的渗透.
【教学方法】观察发现法 诱思探究法 适时点拨法
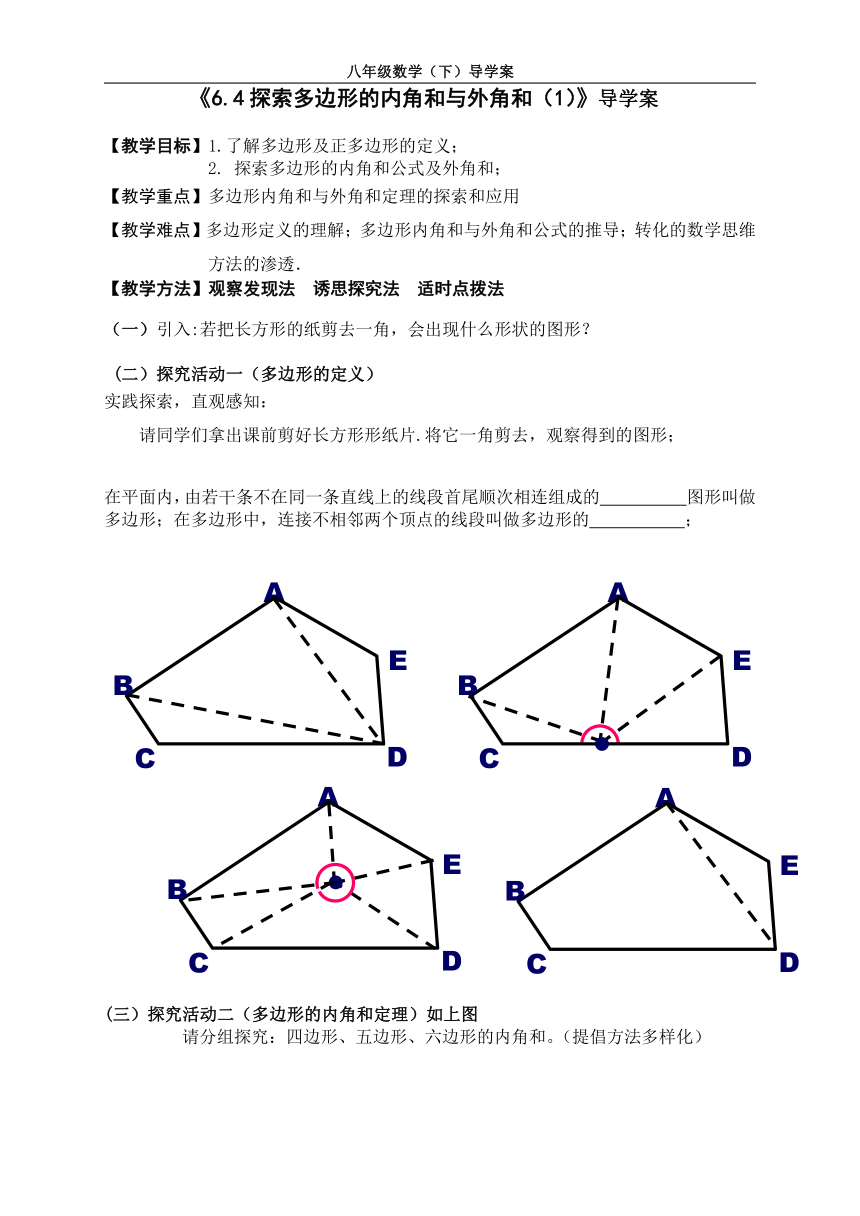
(一)引入:若把长方形的纸剪去一角,会出现什么形状的图形?
(二)探究活动一(多边形的定义)
实践探索,直观感知:
请同学们拿出课前剪好长方形形纸片.将它一角剪去,观察得到的图形;
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的 图形叫做多边形;在多边形中,连接不相邻两个顶点的线段叫做多边形的 ;
(三)探究活动二(多边形的内角和定理)如上图
请分组探究:四边形、五边形、六边形的内角和。(提倡方法多样化)
四边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
五边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
六边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
······
边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
大胆猜想:边形的内角和等于 ;
例1:如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
(四)探究活动三(探索多边形的外角和)
提示:(利用外角与内角的关系)
结论:多边形的外角和都等于360度。
例2:(1)一个多边形每个内角的度数是140°,则这个多边形是几边形?(两种方法)
(2)一个正多边形每个外角都是,求这个多边形的边数;
(3)一个多边形的内角和是外角和的2倍,求这个多边形的边数;
当堂检测
正八边形的内角和为_______.
2一个多边形的内角和等于,这个多边形是几边形?
3.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形.这个多边形是几边形?它的内角和是多少?
4.如图:(1)作多边形所有过顶点A的对角线,并分别用字母表示出来;
(2)求这个多边形的内角和;
(五)课堂小结:
(六)教后反思:
《6.4探索多边形的内角和与外角和(1)》课后巩固
班级 姓名 组别
A基础演练
1.下列各角能成为多边形的内角和的是( )
A B C D
2.(2n+2)边形的外角和(n为大于1的整数)为( )
A B C D
3.如果一个正多边形的内角和为,则这个正多边形是正 边形;
4.一个多边形的内角和与外角和的差是,那么这个多边形是几边形?
B.能力提升
5.四边形的外角中,最多有 个钝角,最多有 个锐角;
6.每个外角都相等的多边形,如果它的一个内角与一个外角的比是2:3,求这个多边形的边数.
7.小明想为世博会设计一个内角和是2011°的多边形花坛,小明的这个想法能实现吗?
《6.4探索多边形的内角和与外角和(1)》导学案
【教学目标】1.了解多边形及正多边形的定义;
2. 探索多边形的内角和公式及外角和;
【教学重点】多边形内角和与外角和定理的探索和应用
【教学难点】多边形定义的理解;多边形内角和与外角和公式的推导;转化的数学思维方法的渗透.
【教学方法】观察发现法 诱思探究法 适时点拨法
(一)引入:若把长方形的纸剪去一角,会出现什么形状的图形?
(二)探究活动一(多边形的定义)
实践探索,直观感知:
请同学们拿出课前剪好长方形形纸片.将它一角剪去,观察得到的图形;
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的 图形叫做多边形;在多边形中,连接不相邻两个顶点的线段叫做多边形的 ;
(三)探究活动二(多边形的内角和定理)如上图
请分组探究:四边形、五边形、六边形的内角和。(提倡方法多样化)
四边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
五边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
六边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
······
边形过一个顶点的所有对角线将它分成了 个三角形,内角和为 ;
大胆猜想:边形的内角和等于 ;
例1:如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
(四)探究活动三(探索多边形的外角和)
提示:(利用外角与内角的关系)
结论:多边形的外角和都等于360度。
例2:(1)一个多边形每个内角的度数是140°,则这个多边形是几边形?(两种方法)
(2)一个正多边形每个外角都是,求这个多边形的边数;
(3)一个多边形的内角和是外角和的2倍,求这个多边形的边数;
当堂检测
正八边形的内角和为_______.
2一个多边形的内角和等于,这个多边形是几边形?
3.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形.这个多边形是几边形?它的内角和是多少?
4.如图:(1)作多边形所有过顶点A的对角线,并分别用字母表示出来;
(2)求这个多边形的内角和;
(五)课堂小结:
(六)教后反思:
《6.4探索多边形的内角和与外角和(1)》课后巩固
班级 姓名 组别
A基础演练
1.下列各角能成为多边形的内角和的是( )
A B C D
2.(2n+2)边形的外角和(n为大于1的整数)为( )
A B C D
3.如果一个正多边形的内角和为,则这个正多边形是正 边形;
4.一个多边形的内角和与外角和的差是,那么这个多边形是几边形?
B.能力提升
5.四边形的外角中,最多有 个钝角,最多有 个锐角;
6.每个外角都相等的多边形,如果它的一个内角与一个外角的比是2:3,求这个多边形的边数.
7.小明想为世博会设计一个内角和是2011°的多边形花坛,小明的这个想法能实现吗?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
