沪科版七年级数学下册课件8.3.1完全平方公式(27张)
文档属性
| 名称 | 沪科版七年级数学下册课件8.3.1完全平方公式(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 19:35:22 | ||
图片预览





文档简介
课件27张PPT。第八章 整式乘法
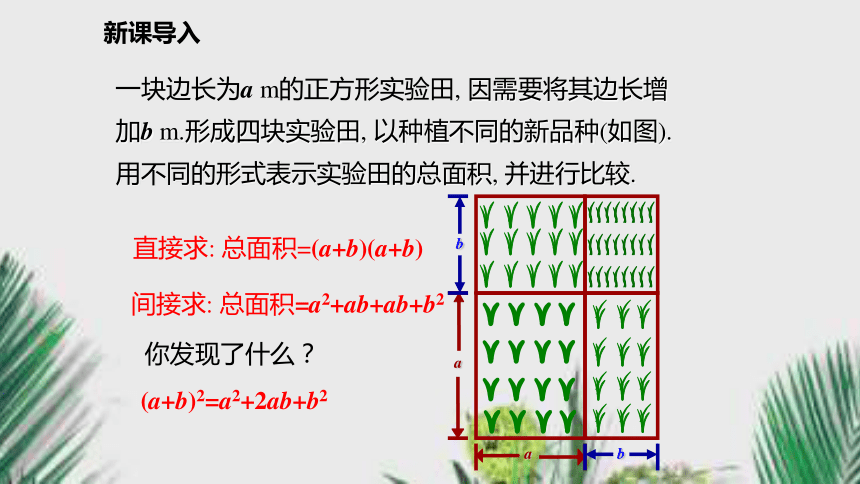
与因式分解七年级数学沪科版·下册8.3.1 完全平方公式新课导入一块边长为a m的正方形实验田, 因需要将其边长增加b m.形成四块实验田, 以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
直接求: 总面积=(a+b)(a+b)间接求: 总面积=a2+ab+ab+b2你发现了什么?(a+b)2=a2+2ab+b2新知探究问题1 计算下列多项式的积, 你能发现什么规律?(1)(p+1)2=(p+1)(p+1)= ;p2+2p+1(2)(m+2)2=(m+2)(m+2)= ;m2+4m+4(3)(p-1)2=(p-1)(p-1)= ;p2-2p+1(4)(m-2)2=(m-2)(m-2)= .m2-4m+4问题2 根据你发现的规律, 你能写出下列式子的答案吗?(a+b)2= ;a2+2ab+b2(a-b)2= .a2-2ab+b2新知探究完全平方公式也就是说, 两个数的和(或差)的平方, 等于它们的平方和, 加上(或减去)它们的积的2倍. 这两个公式叫做(乘法的)完全平方公式.简记为
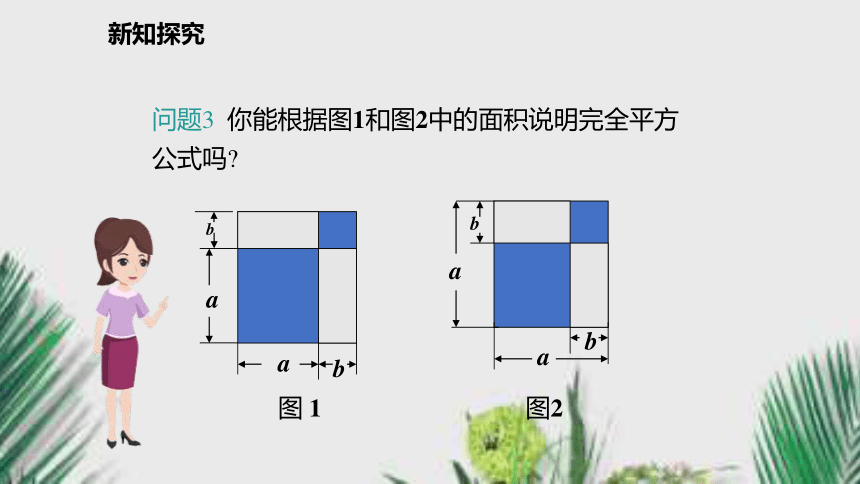
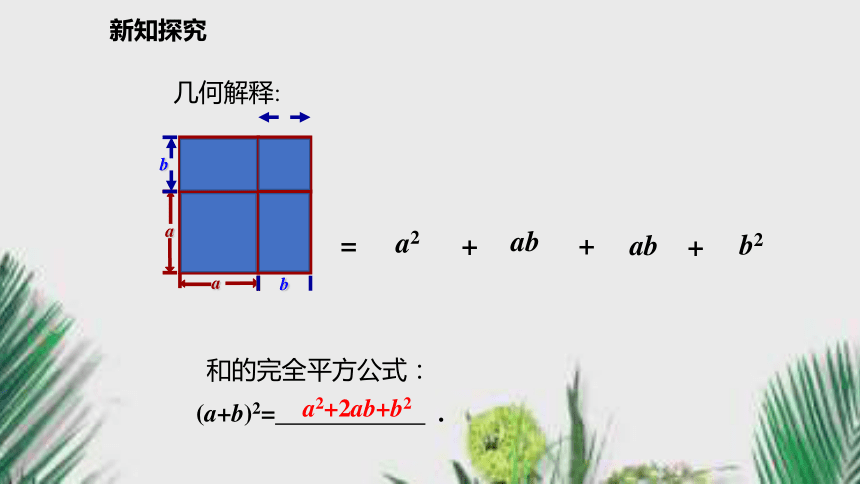
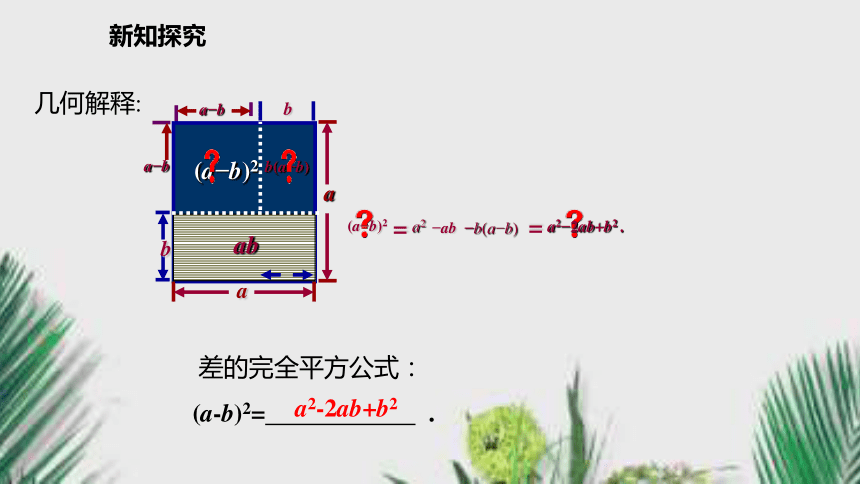
“首平方, 尾平方, 积的2倍放中央”新知探究问题3 你能根据图1和图2中的面积说明完全平方公式吗?新知探究几何解释:=+++和的完全平方公式:a2ababb2新知探究a2?ab?b(a?b)=a2?2ab+b2 .=(a?b)2a?ba?bb(a?b)(a?b)2几何解释:差的完全平方公式:新知探究(a+b)2= a2+2ab+b2.(a-b)2= a2-2ab+b2.问题4 观察下面两个完全平方式, 比一比, 回答下列问题:1.说一说积的次数和项数.2.两个完全平方式的积有相同的项吗? 与a, b有
什么关系?3.两个完全平方式的积中不同的是哪一项? 与 a,
b有什么关系?它的符号与什么有关?新知探究4.公式中的字母a, b可以表示数, 单项式和多项式.1.积为二次三项式;2.积中相同的两项为两数的平方和;3.不同的一项是两数积的2倍, 且与两数中间的符号相同. 公式特征:新知探究 想一想:下面各式的计算是否正确?如果不正确,应当怎样改正?(1)(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3) (-x +y)2 =x2+2xy +y2(4) (2x+y)2 =4x2 +2xy +y2××××(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2 (-x +y)2 =x2 -2xy +y2 (2x +y)2 =4x2+4xy +y2新知探究例1 运用完全平方公式计算.解: (4m+n)2==16m2(1)(4m+n)2;(a+b)2= a2 + 2ab + b2(4m)2+2?(4m) ?n+n2+8mn+n2.新知探究(a - b)2 =a2 -2ab +b2y2解: =新知探究利用完全平方公式计算.
(1)(5-a)2; (2)(-3m-4n)2;
(3)(-3a+b)2.(3)(-3a+b)2=9a2-6ab+b2.解:(1)(5-a)2=25-10a+a2.(2)(-3m-4n)2=9m2+24mn+16n2.新知探究(1) 1022;解: 1022= (100+2)2=10000+400+4=10404.(2) 992.992= (100 –1)2=10000 -200+1=9801. 例2 运用完全平方公式计算:方法总结: 运用完全平方公式进行简便计算, 要熟记完全平方公式的特征, 将原式转化为能利用完全平方公式的形式.新知探究利用乘法公式计算:
(1)982-101×99;
(2)20162-2016×4030+20152.=(2016-2015)2=1.解:(1)原式=(100-2)2-(100+1)(100-1)=1002-400+4-1002+1=-395.(2)原式=20162-2×2016×2015+20152新知探究例3 已知x-y=6, xy=-8. 求:
(1) x2+y2的值; (2)(x+y)2的值.=36-16=20. 解: (1)因为x-y=6, xy=-8,(x-y)2=x2+y2-2xy,所以x2+y2=(x-y)2+2xy(2)因为x2+y2=20, xy=-8,所以(x+y)2=x2+y2+2xy=20-16=4.新知探究方法总结:
本题要熟练掌握完全平方公式的变式:
x2+y2=(x-y)2+2xy=(x+y)2-2xy,(x-y)2=(x+y)2-4xy.新知探究a+(b+c) = a+b+c;
a- (b+c) = a - b – c.a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .去括号把上面两个等式的左右两边反过来, 也就添括号.新知探究 添括号时, 如果括号前面是正号, 括到括号里的各项都不变号; 如果括号前面是负号, 括到括号里的各项都改变符号(简记为 “负变正不变”).知识要点添括号法则新知探究例4 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ; (2) (a+b+c)2.
(2)原式 = [(a+b)+c]2 = x2-(2y-3)2 = x2-(4y2-12y+9)= x2-4y2+12y-9.= (a+b)2+2(a+b)c+c2=a2+2ab+b2+2ac+2bc+c2.新知探究方法总结: 第1小题选用平方差公式进行计算, 需要分组. 分组方法是 “符号相同的为一组, 符号相反的为另一组” ; 第2小题要把其中两项看成一个整体, 再按照完全平方公式进行计算.新知探究计算:(1)(a-b+c)2;
(2)(1-2x+y)(1+2x-y).=1-4x2+4xy-y2.解:(1)原式=[(a-b)+c]2=(a-b)2+c2+2(a-b)c=a2-2ab+b2+c2+2ac-2bc.(2)原式=[1+(-2x+y)][1-(-2x+y)]=12-(-2x+y)2课堂小结完全平方公式法则注意(a ± b)2= a2 ± 2ab + b21.项数、符号、字母及其指数2.不能直接应用公式进行计算的式子, 可能需要先添括号变形成符合公式的要求才行常用
结论3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2课堂小测2.下列计算结果为2ab-a2-b2的是 ( )
A.(a-b)2 B.(-a-b)2
C.-(a+b)2 D.-(a-b)21.运用乘法公式计算(a-2)2的结果是( )
A.a2-4a+4 B.a2-2a+4
C.a2-4 D.a2-4a-4 AD课堂小测3.运用完全平方公式计算:(1) (6a+5b)2=_______________;
(2) (4x-3y)2=_______________;
(3) (2m-1)2 =_______________;
(4) (-2m-1)2 =_______________.36a2+60ab+25b216x2-24xy+9y24m2+4m+1 4m2-4m+14.由完全平方公式可知32+2×3×5+52=(3+5)2=64,运用这一方法计算4.3212+8.642×0.679+0.6792=________. 25课堂小测5.计算.
(1)(3a+b-2)(3a-b+2);
(2)(x-y-m+n)(x-y+m-n).(2)原式=[(x-y)-(m-n)][(x-y)+(m-n)]解: (1)原式=[3a+(b-2)][3a-(b-2)]=(3a)2-(b-2)2=9a2-b2+4b-4. =(x-y)2-(m-n)2=x2-2xy+y2-m2+2mn-n2.课堂小测6.若a+b=5, ab=-6, 求 a2+b2, a2-ab+b2.
7.已知x+y=8, x-y=4, 求 xy.解: a2+b2=(a+b)2-2ab=52-2×(-6)=37;a2-ab+b2=a2+b2-ab=37-(-6)=43.解:因为x+y=8, 所以(x+y)2=64, 即x2+y2+2xy=64.①因为x-y=4, 所以(x-y)2=16, 即x2+y2-2xy=16.②由①-②,得4xy=48,所以 xy=12.
直接求: 总面积=(a+b)(a+b)间接求: 总面积=a2+ab+ab+b2你发现了什么?(a+b)2=a2+2ab+b2新知探究问题1 计算下列多项式的积, 你能发现什么规律?(1)(p+1)2=(p+1)(p+1)= ;p2+2p+1(2)(m+2)2=(m+2)(m+2)= ;m2+4m+4(3)(p-1)2=(p-1)(p-1)= ;p2-2p+1(4)(m-2)2=(m-2)(m-2)= .m2-4m+4问题2 根据你发现的规律, 你能写出下列式子的答案吗?(a+b)2= ;a2+2ab+b2(a-b)2= .a2-2ab+b2新知探究完全平方公式也就是说, 两个数的和(或差)的平方, 等于它们的平方和, 加上(或减去)它们的积的2倍. 这两个公式叫做(乘法的)完全平方公式.简记为
“首平方, 尾平方, 积的2倍放中央”新知探究问题3 你能根据图1和图2中的面积说明完全平方公式吗?新知探究几何解释:=+++和的完全平方公式:a2ababb2新知探究a2?ab?b(a?b)=a2?2ab+b2 .=(a?b)2a?ba?bb(a?b)(a?b)2几何解释:差的完全平方公式:新知探究(a+b)2= a2+2ab+b2.(a-b)2= a2-2ab+b2.问题4 观察下面两个完全平方式, 比一比, 回答下列问题:1.说一说积的次数和项数.2.两个完全平方式的积有相同的项吗? 与a, b有
什么关系?3.两个完全平方式的积中不同的是哪一项? 与 a,
b有什么关系?它的符号与什么有关?新知探究4.公式中的字母a, b可以表示数, 单项式和多项式.1.积为二次三项式;2.积中相同的两项为两数的平方和;3.不同的一项是两数积的2倍, 且与两数中间的符号相同. 公式特征:新知探究 想一想:下面各式的计算是否正确?如果不正确,应当怎样改正?(1)(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3) (-x +y)2 =x2+2xy +y2(4) (2x+y)2 =4x2 +2xy +y2××××(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2 (-x +y)2 =x2 -2xy +y2 (2x +y)2 =4x2+4xy +y2新知探究例1 运用完全平方公式计算.解: (4m+n)2==16m2(1)(4m+n)2;(a+b)2= a2 + 2ab + b2(4m)2+2?(4m) ?n+n2+8mn+n2.新知探究(a - b)2 =a2 -2ab +b2y2解: =新知探究利用完全平方公式计算.
(1)(5-a)2; (2)(-3m-4n)2;
(3)(-3a+b)2.(3)(-3a+b)2=9a2-6ab+b2.解:(1)(5-a)2=25-10a+a2.(2)(-3m-4n)2=9m2+24mn+16n2.新知探究(1) 1022;解: 1022= (100+2)2=10000+400+4=10404.(2) 992.992= (100 –1)2=10000 -200+1=9801. 例2 运用完全平方公式计算:方法总结: 运用完全平方公式进行简便计算, 要熟记完全平方公式的特征, 将原式转化为能利用完全平方公式的形式.新知探究利用乘法公式计算:
(1)982-101×99;
(2)20162-2016×4030+20152.=(2016-2015)2=1.解:(1)原式=(100-2)2-(100+1)(100-1)=1002-400+4-1002+1=-395.(2)原式=20162-2×2016×2015+20152新知探究例3 已知x-y=6, xy=-8. 求:
(1) x2+y2的值; (2)(x+y)2的值.=36-16=20. 解: (1)因为x-y=6, xy=-8,(x-y)2=x2+y2-2xy,所以x2+y2=(x-y)2+2xy(2)因为x2+y2=20, xy=-8,所以(x+y)2=x2+y2+2xy=20-16=4.新知探究方法总结:
本题要熟练掌握完全平方公式的变式:
x2+y2=(x-y)2+2xy=(x+y)2-2xy,(x-y)2=(x+y)2-4xy.新知探究a+(b+c) = a+b+c;
a- (b+c) = a - b – c.a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .去括号把上面两个等式的左右两边反过来, 也就添括号.新知探究 添括号时, 如果括号前面是正号, 括到括号里的各项都不变号; 如果括号前面是负号, 括到括号里的各项都改变符号(简记为 “负变正不变”).知识要点添括号法则新知探究例4 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ; (2) (a+b+c)2.
(2)原式 = [(a+b)+c]2 = x2-(2y-3)2 = x2-(4y2-12y+9)= x2-4y2+12y-9.= (a+b)2+2(a+b)c+c2=a2+2ab+b2+2ac+2bc+c2.新知探究方法总结: 第1小题选用平方差公式进行计算, 需要分组. 分组方法是 “符号相同的为一组, 符号相反的为另一组” ; 第2小题要把其中两项看成一个整体, 再按照完全平方公式进行计算.新知探究计算:(1)(a-b+c)2;
(2)(1-2x+y)(1+2x-y).=1-4x2+4xy-y2.解:(1)原式=[(a-b)+c]2=(a-b)2+c2+2(a-b)c=a2-2ab+b2+c2+2ac-2bc.(2)原式=[1+(-2x+y)][1-(-2x+y)]=12-(-2x+y)2课堂小结完全平方公式法则注意(a ± b)2= a2 ± 2ab + b21.项数、符号、字母及其指数2.不能直接应用公式进行计算的式子, 可能需要先添括号变形成符合公式的要求才行常用
结论3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2课堂小测2.下列计算结果为2ab-a2-b2的是 ( )
A.(a-b)2 B.(-a-b)2
C.-(a+b)2 D.-(a-b)21.运用乘法公式计算(a-2)2的结果是( )
A.a2-4a+4 B.a2-2a+4
C.a2-4 D.a2-4a-4 AD课堂小测3.运用完全平方公式计算:(1) (6a+5b)2=_______________;
(2) (4x-3y)2=_______________;
(3) (2m-1)2 =_______________;
(4) (-2m-1)2 =_______________.36a2+60ab+25b216x2-24xy+9y24m2+4m+1 4m2-4m+14.由完全平方公式可知32+2×3×5+52=(3+5)2=64,运用这一方法计算4.3212+8.642×0.679+0.6792=________. 25课堂小测5.计算.
(1)(3a+b-2)(3a-b+2);
(2)(x-y-m+n)(x-y+m-n).(2)原式=[(x-y)-(m-n)][(x-y)+(m-n)]解: (1)原式=[3a+(b-2)][3a-(b-2)]=(3a)2-(b-2)2=9a2-b2+4b-4. =(x-y)2-(m-n)2=x2-2xy+y2-m2+2mn-n2.课堂小测6.若a+b=5, ab=-6, 求 a2+b2, a2-ab+b2.
7.已知x+y=8, x-y=4, 求 xy.解: a2+b2=(a+b)2-2ab=52-2×(-6)=37;a2-ab+b2=a2+b2-ab=37-(-6)=43.解:因为x+y=8, 所以(x+y)2=64, 即x2+y2+2xy=64.①因为x-y=4, 所以(x-y)2=16, 即x2+y2-2xy=16.②由①-②,得4xy=48,所以 xy=12.
