沪科版七年级数学下册课件8.3.3乘法公式的应用(12张)
文档属性
| 名称 | 沪科版七年级数学下册课件8.3.3乘法公式的应用(12张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-31 19:38:42 | ||
图片预览



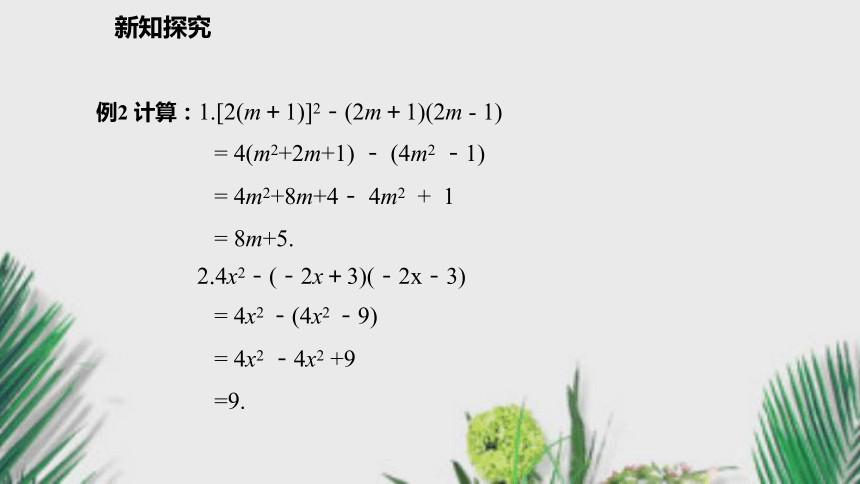


文档简介
课件12张PPT。第八章 整式乘法
与因式分解七年级数学沪科版·下册8.3.3 乘法公式的应用新课导入 1.(x+3)(x-3)= 2.( 2x+5)2 = 3.(a2+b2)(a2 -b2)= 4.(-3m+4n)2=x2-9.4x2+20x+25.a4 -b4.9m2 -24mn+16m2.新知探究解:=-4xy.你能说出每一步运用的理论依据吗?新知探究例2 计算:1.[2(m+1)]2-(2m+1)(2m - 1) 2.4x2-(-2x+3)(-2x-3)= 4(m2+2m+1) - (4m2 -1)
= 4m2+8m+4- 4m2 + 1
= 8m+5.= 4x2 -(4x2 -9)
= 4x2 -4x2 +9
=9.新知探究例3 计算:(a+2b+3c)(a+2b-3c)解:(a+2b+3c)(a+2b-3c)=[(a+2b)+3c][(a+2b)-3c)]=(a+2b)2 -(3c)2=a2+4ab+4b2-9c2.
新知探究例4 计算:(a+b)3 解: (a+b)3 =(a+b)(a+b)2
= (a+b)(a2+2ab+b2)
=a3+2a2b+ab2+a2b+2ab2+b3
=a3+3a2b+3ab2+b3.
新知探究例5 计算: 1.(2a-3b+c)(2a - 3b -c) 2.(x+y+z)(x-y-z)=(2a - 3b )2 -c2= x2 -(y+z)2= x2 -(y2+2yz+z2) = x2 -y2 - 2yz - z2.=4a2-12ab + 9b2 - c2.
新知探究课堂小结完全平方公式平方差公式?课堂小测√√1.判断并改错.;;.课堂小测-2x4-4ab-2ab2.填空.;;.;课堂小测3.观察下列各式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1.
根据前面各式的规律可得(x-1)(xn+xn-1+…+x+1)
= (其中n为正整数).xn+1-1
= 4m2+8m+4- 4m2 + 1
= 8m+5.= 4x2 -(4x2 -9)
= 4x2 -4x2 +9
=9.新知探究例3 计算:(a+2b+3c)(a+2b-3c)解:(a+2b+3c)(a+2b-3c)=[(a+2b)+3c][(a+2b)-3c)]=(a+2b)2 -(3c)2=a2+4ab+4b2-9c2.
新知探究例4 计算:(a+b)3 解: (a+b)3 =(a+b)(a+b)2
= (a+b)(a2+2ab+b2)
=a3+2a2b+ab2+a2b+2ab2+b3
=a3+3a2b+3ab2+b3.
新知探究例5 计算: 1.(2a-3b+c)(2a - 3b -c) 2.(x+y+z)(x-y-z)=(2a - 3b )2 -c2= x2 -(y+z)2= x2 -(y2+2yz+z2) = x2 -y2 - 2yz - z2.=4a2-12ab + 9b2 - c2.
新知探究课堂小结完全平方公式平方差公式?课堂小测√√1.判断并改错.;;.课堂小测-2x4-4ab-2ab2.填空.;;.;课堂小测3.观察下列各式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1.
根据前面各式的规律可得(x-1)(xn+xn-1+…+x+1)
= (其中n为正整数).xn+1-1
