必修2 高二数学 第二章 2.3.2平面与平面垂直的判定 教学课件(共31张PPT)
文档属性
| 名称 | 必修2 高二数学 第二章 2.3.2平面与平面垂直的判定 教学课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 419.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 14:12:57 | ||
图片预览






文档简介
(共31张PPT)
新课导入
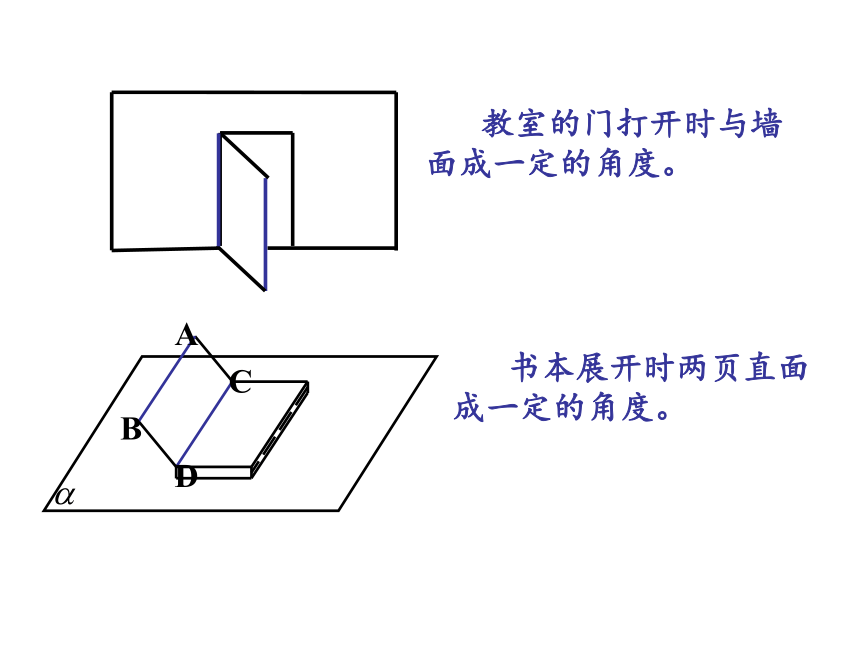
修水坝时,为了使水坝坚固耐用,必须使水坝面与水平面成一定的角度。
砌墙时,要保证墙面与地面垂直。
B
A
C
D
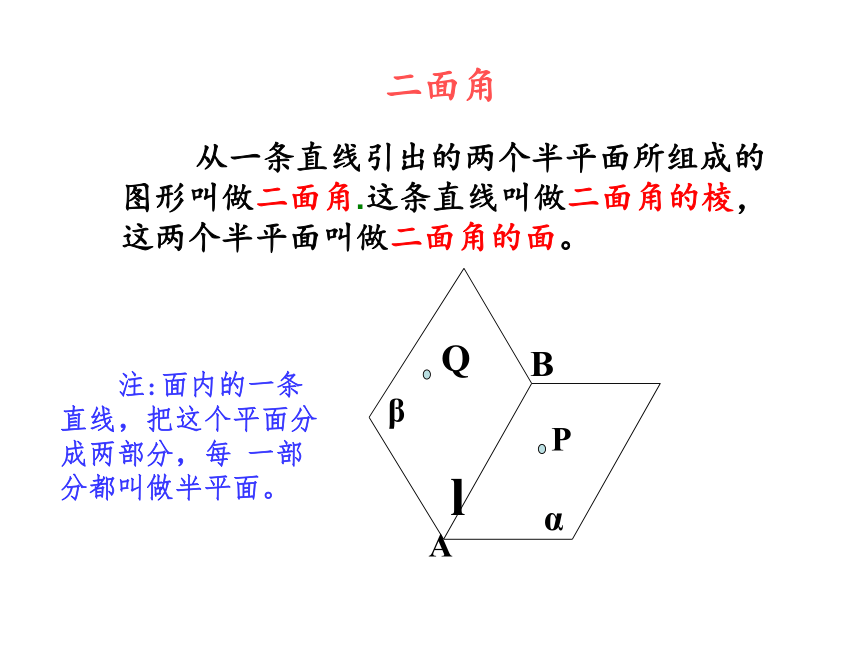
教室的门打开时与墙面成一定的角度。
书本展开时两页直面成一定的角度。
2.3.2 平面与平面垂直的判定
教学目标
知识与能力
使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念。
使学生掌握两个平面垂直的判定定理及其简单的应用。
过程与方法
情感态度与价值观
通过实例让学生直观感知“二面角”概念的形成过程。
类比已学知识,归纳“二面角”的度量方法及两个平面垂直的判定定理。
通过揭示概念的形成、发展和应用过程,使学生理会教学存在于观实生活周围,从中激发学生积极思维,培养学生的观察、分析、解决问题能力。
教学重难点
重点
难点
平面与平面垂直的判定。
如何度量二面角的大小。
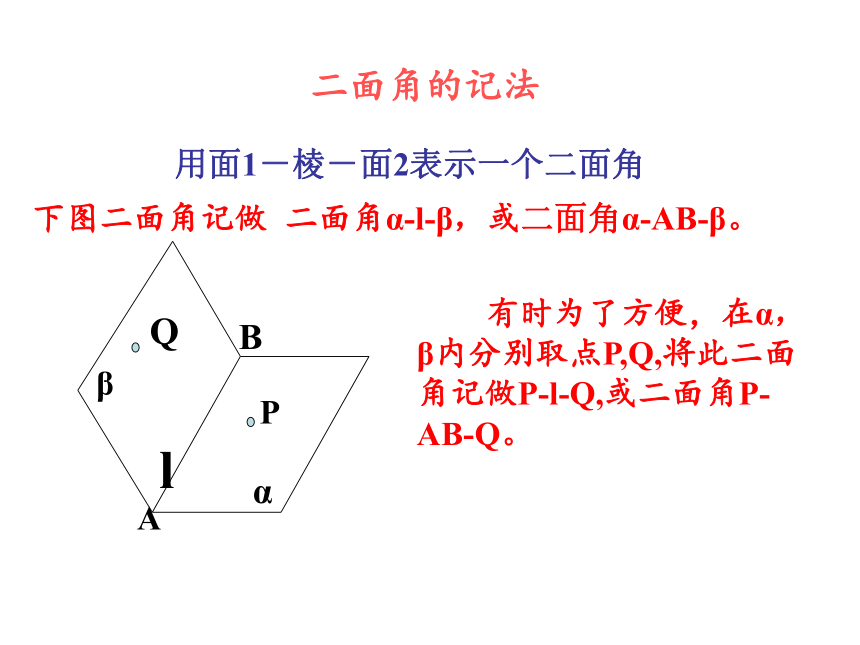
从一条直线引出的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
二面角
注:面内的一条直线,把这个平面分成两部分,每 一部分都叫做半平面。
二面角的记法
下图二面角记做 二面角α-l-β,或二面角α-AB-β。
用面1-棱-面2表示一个二面角
有时为了方便,在α,β内分别取点P,Q,将此二面角记做P-l-Q,或二面角P-AB-Q。
l
β
α
A
B
?
?
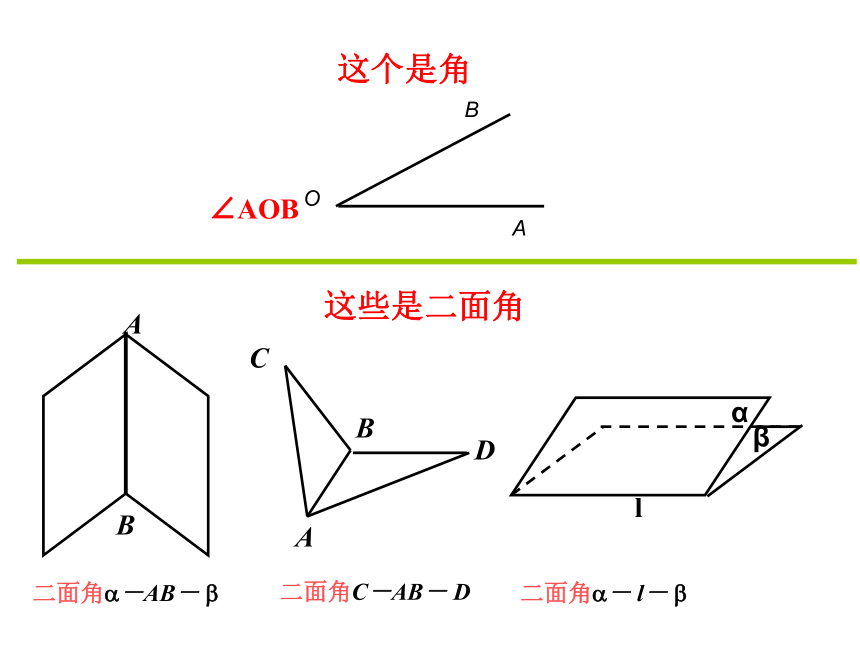
二面角?-AB- ?
二面角?- l- ?
二面角C-AB- D
A
B
C
D
O
B
A
∠AOB
这个是角
这些是二面角
角
B
A
O
边
边
顶点
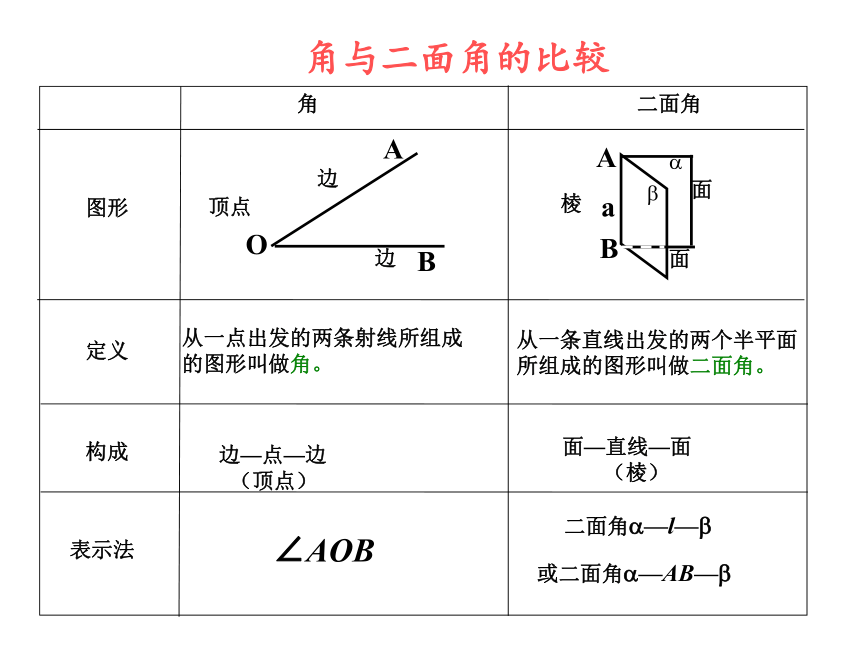
从一点出发的两条射线所组成的图形叫做角。
定义
构成
边—点—边
(顶点)
表示法
∠AOB
二面角
A
B
面
面
棱
a
?
?
从一条直线出发的两个半平面所组成的图形叫做二面角。
面—直线—面
(棱)
二面角?—l—?
或二面角?—AB—?
图形
角与二面角的比较
?
?
?
?
?
?
?
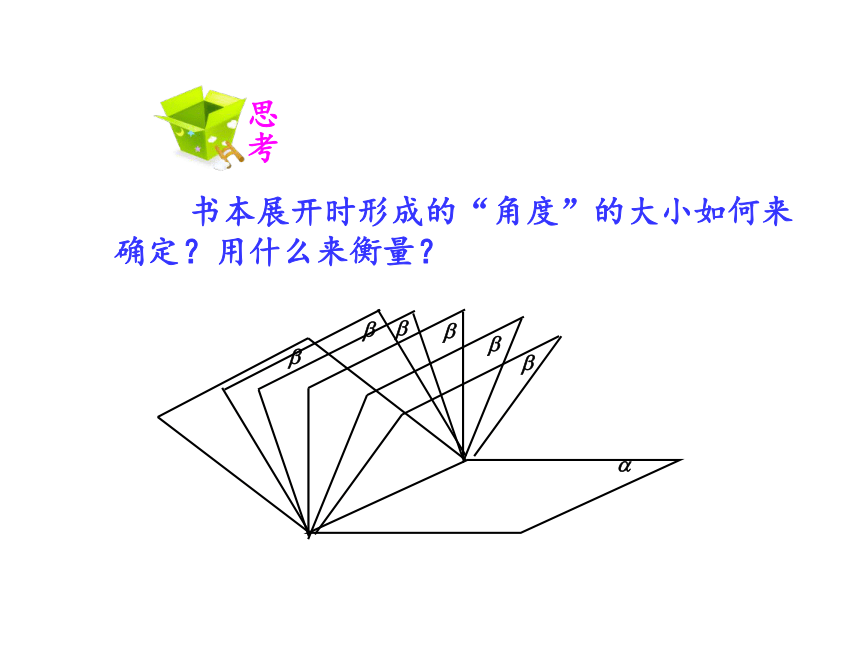
书本展开时形成的“角度”的大小如何来确定?用什么来衡量?
思考
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
二面角的平面角
二面角的平面角必须满足:
3)角的边都要垂直于二面角的棱
1)角的顶点在棱上
2)角的两边分别在两个面内
?
?
l
O
A
B
?
?
A
O
B
是二面角
不是二面角
二面角的平面角用来度量二面角的大小,二面角是多少度,就说这个二面角是多少度。
上图是正方体ABCD-A‘B’C‘D’,二面角 度数为45°。
当二面角的两个面重合时,二面角的大小为多少度?当二面角的两个面合成一个平面时,二面角的大小为多少度?一般地,二面角的平面角的取值范围如何?
思考
二面角为0°
二面角为90°
二面角的取值范围是[0, ]。
平面角是直角的二面角叫做直二面角。
若两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
记作:
两个平面互相垂直
如何检测所砌的墙面和地面是否垂直?
思考
可以用铅垂判断所在直线是否与地面垂直。
平面和平面垂直的判定定理
符号表示:
如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直。
线线垂直
线面垂直
面面垂直
α
β
C
D
A
B
E
证明:设α∩β=CD,则B∈CD.
∵AB⊥β,CD β,∴AB⊥CD.
在平面β内过B点作直线BE⊥CD,则∠ABE就是二面角
平面角,
∪
已知:AB⊥β,
求证: ⊥β。
定理证明
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角 是直二面角,
∴ ⊥β.
证明:设α∩β=CD,则B∈CD。
∵AB⊥β,CD β,∴AB⊥CD.
在平面β内过B点作直线BE⊥CD,则∠ABE就是二面角
平面角,
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角 是直二面角,
∴ ⊥β.
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角 是直二面角,
∴ ⊥β。
在正方体A C1中 ,求证 :平面A1C1CA ⊥平面B1D1DB
A
B
C
C1
D
B1
A1
D1
例四
证明:∵AA1⊥面AC,
∴AA1⊥BD,
又∵BD⊥AC,
∴BD⊥面ACC1A1,
∴平面A1C1CA ⊥平面B1D1DB
例五
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC。
B
P
A
C
O
证明:∵在圆o中AB为直径,
∴AC⊥BC,
又∵PA⊥面ABC,
∴PA⊥BC,
∴BC ⊥平面PAC,
∴平面PAC⊥平面PBC。
课堂小结
从一条直线引出的两个半平面所组成的图形叫做二面角。二面角的平面角用来度量二面角的大小。
平面角是直角的二面角叫做直二面角。
平面和平面垂直的判定定理:
如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直。
A
B
D
C
线面垂直
面面垂直
随堂练习
1)如果平面α内有一条直线垂直于平面β内的一条直线,则α⊥β( )
3)如果平面α内的一条直线垂直于平面β内的两条相交直线, 则α⊥β( )
1. 判断:
×
×
√
2)如果平面α内有一条直线垂直于平面β内的两条直线,则α⊥β( )
√
4)若m⊥α,m β,则α⊥β( )
1)过平面α的一条垂线可作个________平面与平面α垂直。
2)过一点可作_____个平面与已知平面垂直。
2. 填空:
3)过平面α的一条斜线,可作____个平面与平面α垂直。
4)过平面α的一条平行线可作____个平面与α垂直。
一
无数
无数
一
1)给出下列四个命题:
①垂直于同一个平面的两个平面平行;
②垂直于同一条直线的两个平面平行;
③垂直于同一个平面的两条直线平行;
④垂直于同一条直线的两条直线平行。
其中正确的命题的个数是(????? )
A.1???????? B.2?????????? C.3?????????? D.4
B?
3. 选择:
2)给出下列四个命题:(其中a,b表直线,α,β,γ表平面)
①若a⊥b,a∥α,则b⊥α;
②若a∥α,α⊥β,则a⊥β;
③若β∥γ,α∥γ,则α⊥β;
④若α⊥β,a⊥β,则a∥α其中不正确的命题的个数是(????? )
A.1???????? B.2??????????? C.3????????? D.4
D
A
B
C
D
A1
B1
C1
D1
4.在正方体ABCD-A1B1C1D1中,
求证:平面ACC1A1⊥平面A1BD。
证明:∵AA1⊥面AC,
∴AA1⊥BD
又∵BD⊥AC,
∴BD⊥平面ACC1A1
∴平面ACC1A1⊥平面A1BD。
A
α
B
β
O
C
5.在二面角α-l-β的一个面α内有一条直线AB,若AB与棱l的夹角为45°,AB与平面β所成的角为30°,则此二面角的大小是多少?
如图,过A点作AO⊥β于O,在α内作AC垂直棱于C,连OB、OC,则∠ABC=45°,∠ABO=30°,∠ACO就是所求二面角的平面角。
设AB=a,则AC=
,AO=
则sin∠ACO=
∴∠ACO=45°
6.如图:在Rt△ABC中,∠B=900 ,P为△ABC所在平面外一点,PA⊥平面ABC,问:四面体P-ABC中有几个直角三角形?并证明之。
P
A
B
C
四个面都是直角三角形
新课导入
修水坝时,为了使水坝坚固耐用,必须使水坝面与水平面成一定的角度。
砌墙时,要保证墙面与地面垂直。
B
A
C
D
教室的门打开时与墙面成一定的角度。
书本展开时两页直面成一定的角度。
2.3.2 平面与平面垂直的判定
教学目标
知识与能力
使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念。
使学生掌握两个平面垂直的判定定理及其简单的应用。
过程与方法
情感态度与价值观
通过实例让学生直观感知“二面角”概念的形成过程。
类比已学知识,归纳“二面角”的度量方法及两个平面垂直的判定定理。
通过揭示概念的形成、发展和应用过程,使学生理会教学存在于观实生活周围,从中激发学生积极思维,培养学生的观察、分析、解决问题能力。
教学重难点
重点
难点
平面与平面垂直的判定。
如何度量二面角的大小。
从一条直线引出的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
二面角
注:面内的一条直线,把这个平面分成两部分,每 一部分都叫做半平面。
二面角的记法
下图二面角记做 二面角α-l-β,或二面角α-AB-β。
用面1-棱-面2表示一个二面角
有时为了方便,在α,β内分别取点P,Q,将此二面角记做P-l-Q,或二面角P-AB-Q。
l
β
α
A
B
?
?
二面角?-AB- ?
二面角?- l- ?
二面角C-AB- D
A
B
C
D
O
B
A
∠AOB
这个是角
这些是二面角
角
B
A
O
边
边
顶点
从一点出发的两条射线所组成的图形叫做角。
定义
构成
边—点—边
(顶点)
表示法
∠AOB
二面角
A
B
面
面
棱
a
?
?
从一条直线出发的两个半平面所组成的图形叫做二面角。
面—直线—面
(棱)
二面角?—l—?
或二面角?—AB—?
图形
角与二面角的比较
?
?
?
?
?
?
?
书本展开时形成的“角度”的大小如何来确定?用什么来衡量?
思考
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
二面角的平面角
二面角的平面角必须满足:
3)角的边都要垂直于二面角的棱
1)角的顶点在棱上
2)角的两边分别在两个面内
?
?
l
O
A
B
?
?
A
O
B
是二面角
不是二面角
二面角的平面角用来度量二面角的大小,二面角是多少度,就说这个二面角是多少度。
上图是正方体ABCD-A‘B’C‘D’,二面角 度数为45°。
当二面角的两个面重合时,二面角的大小为多少度?当二面角的两个面合成一个平面时,二面角的大小为多少度?一般地,二面角的平面角的取值范围如何?
思考
二面角为0°
二面角为90°
二面角的取值范围是[0, ]。
平面角是直角的二面角叫做直二面角。
若两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
记作:
两个平面互相垂直
如何检测所砌的墙面和地面是否垂直?
思考
可以用铅垂判断所在直线是否与地面垂直。
平面和平面垂直的判定定理
符号表示:
如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直。
线线垂直
线面垂直
面面垂直
α
β
C
D
A
B
E
证明:设α∩β=CD,则B∈CD.
∵AB⊥β,CD β,∴AB⊥CD.
在平面β内过B点作直线BE⊥CD,则∠ABE就是二面角
平面角,
∪
已知:AB⊥β,
求证: ⊥β。
定理证明
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角 是直二面角,
∴ ⊥β.
证明:设α∩β=CD,则B∈CD。
∵AB⊥β,CD β,∴AB⊥CD.
在平面β内过B点作直线BE⊥CD,则∠ABE就是二面角
平面角,
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角 是直二面角,
∴ ⊥β.
∵AB⊥β,BE β,
∴AB⊥BE. ∴二面角 是直二面角,
∴ ⊥β。
在正方体A C1中 ,求证 :平面A1C1CA ⊥平面B1D1DB
A
B
C
C1
D
B1
A1
D1
例四
证明:∵AA1⊥面AC,
∴AA1⊥BD,
又∵BD⊥AC,
∴BD⊥面ACC1A1,
∴平面A1C1CA ⊥平面B1D1DB
例五
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面PAC⊥平面PBC。
B
P
A
C
O
证明:∵在圆o中AB为直径,
∴AC⊥BC,
又∵PA⊥面ABC,
∴PA⊥BC,
∴BC ⊥平面PAC,
∴平面PAC⊥平面PBC。
课堂小结
从一条直线引出的两个半平面所组成的图形叫做二面角。二面角的平面角用来度量二面角的大小。
平面角是直角的二面角叫做直二面角。
平面和平面垂直的判定定理:
如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直。
A
B
D
C
线面垂直
面面垂直
随堂练习
1)如果平面α内有一条直线垂直于平面β内的一条直线,则α⊥β( )
3)如果平面α内的一条直线垂直于平面β内的两条相交直线, 则α⊥β( )
1. 判断:
×
×
√
2)如果平面α内有一条直线垂直于平面β内的两条直线,则α⊥β( )
√
4)若m⊥α,m β,则α⊥β( )
1)过平面α的一条垂线可作个________平面与平面α垂直。
2)过一点可作_____个平面与已知平面垂直。
2. 填空:
3)过平面α的一条斜线,可作____个平面与平面α垂直。
4)过平面α的一条平行线可作____个平面与α垂直。
一
无数
无数
一
1)给出下列四个命题:
①垂直于同一个平面的两个平面平行;
②垂直于同一条直线的两个平面平行;
③垂直于同一个平面的两条直线平行;
④垂直于同一条直线的两条直线平行。
其中正确的命题的个数是(????? )
A.1???????? B.2?????????? C.3?????????? D.4
B?
3. 选择:
2)给出下列四个命题:(其中a,b表直线,α,β,γ表平面)
①若a⊥b,a∥α,则b⊥α;
②若a∥α,α⊥β,则a⊥β;
③若β∥γ,α∥γ,则α⊥β;
④若α⊥β,a⊥β,则a∥α其中不正确的命题的个数是(????? )
A.1???????? B.2??????????? C.3????????? D.4
D
A
B
C
D
A1
B1
C1
D1
4.在正方体ABCD-A1B1C1D1中,
求证:平面ACC1A1⊥平面A1BD。
证明:∵AA1⊥面AC,
∴AA1⊥BD
又∵BD⊥AC,
∴BD⊥平面ACC1A1
∴平面ACC1A1⊥平面A1BD。
A
α
B
β
O
C
5.在二面角α-l-β的一个面α内有一条直线AB,若AB与棱l的夹角为45°,AB与平面β所成的角为30°,则此二面角的大小是多少?
如图,过A点作AO⊥β于O,在α内作AC垂直棱于C,连OB、OC,则∠ABC=45°,∠ABO=30°,∠ACO就是所求二面角的平面角。
设AB=a,则AC=
,AO=
则sin∠ACO=
∴∠ACO=45°
6.如图:在Rt△ABC中,∠B=900 ,P为△ABC所在平面外一点,PA⊥平面ABC,问:四面体P-ABC中有几个直角三角形?并证明之。
P
A
B
C
四个面都是直角三角形
