必修2 高二数学 第一章 1.3.1柱体、椎体、台体的表面积与体积 上课课件(共35张PPT)
文档属性
| 名称 | 必修2 高二数学 第一章 1.3.1柱体、椎体、台体的表面积与体积 上课课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 14:04:05 | ||
图片预览






文档简介
(共35张PPT)
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
导入新课
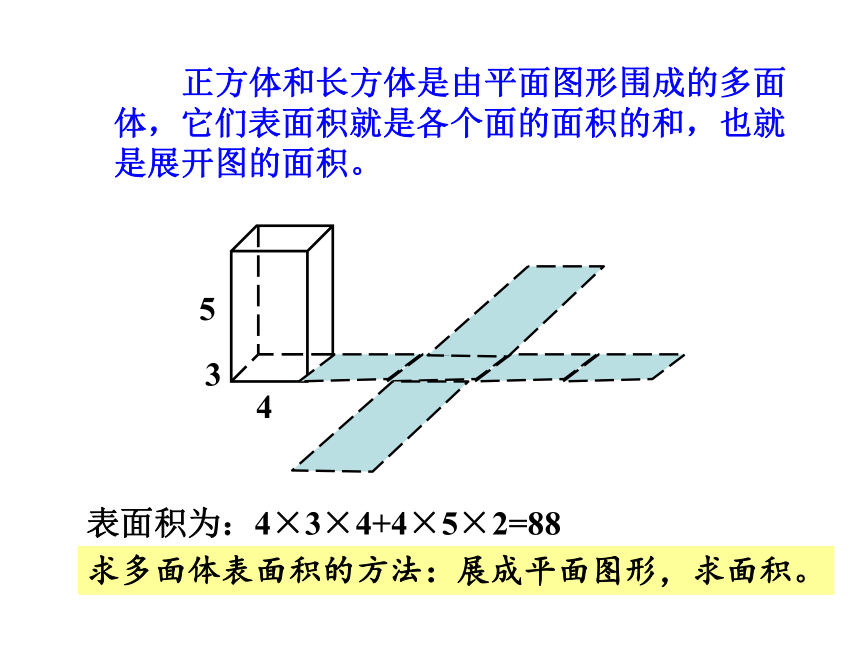
正方体和长方体是由平面图形围成的多面体,它们表面积就是各个面的面积的和,也就是展开图的面积。
5
4
3
表面积为:4×3×4+4×5×2=88
求多面体表面积的方法:展成平面图形,求面积。
1.3.1 柱体、锥体、台体的
表面积与体积
教学目标
知识与能力
通过对柱、锥、台体的研究,掌握柱、锥、台的表面积和体积的求法。
能运用公式求解柱体、锥体和台体的体积,并且熟悉台体与柱体和锥体之间的转换关系。
过程与方法
让学生经历几何全的侧面展一过程,感知几何体的形状。
让学生通对照比较,了解柱体、锥体、台体的面积和体积的关系。
情感态度与价值观
使学生感受到几何体面积和体积的求解过程,对自己空间思维能力影响 。
教学重难点
柱体、锥体、台体的表面积和体积计算。
台体体积公式的推导。
重点
难点
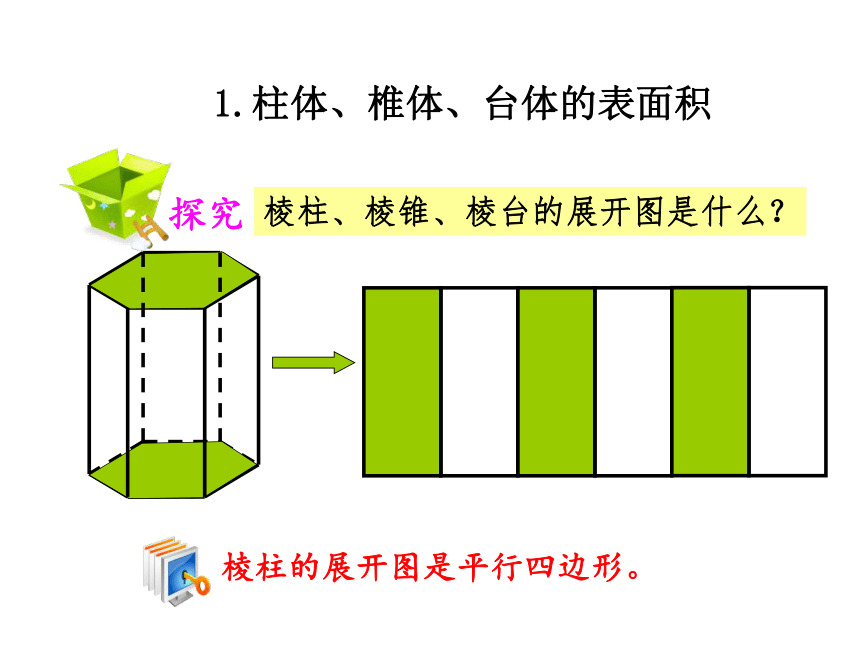
探究
棱柱、棱锥、棱台的展开图是什么?
棱柱的展开图是平行四边形。
1.柱体、椎体、台体的表面积
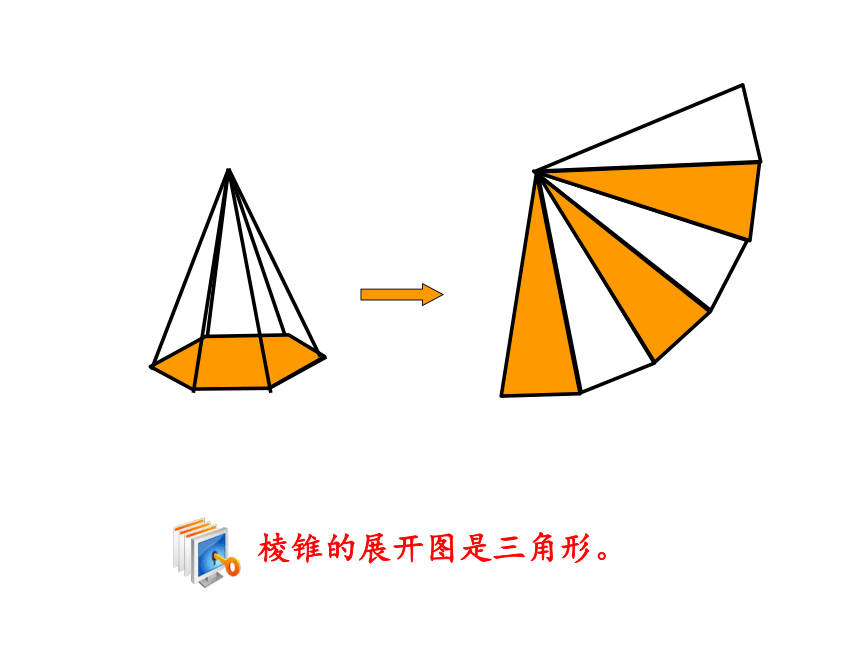
棱锥的展开图是三角形。
同理,棱台的展开图呢?
棱台的展开图是梯形。
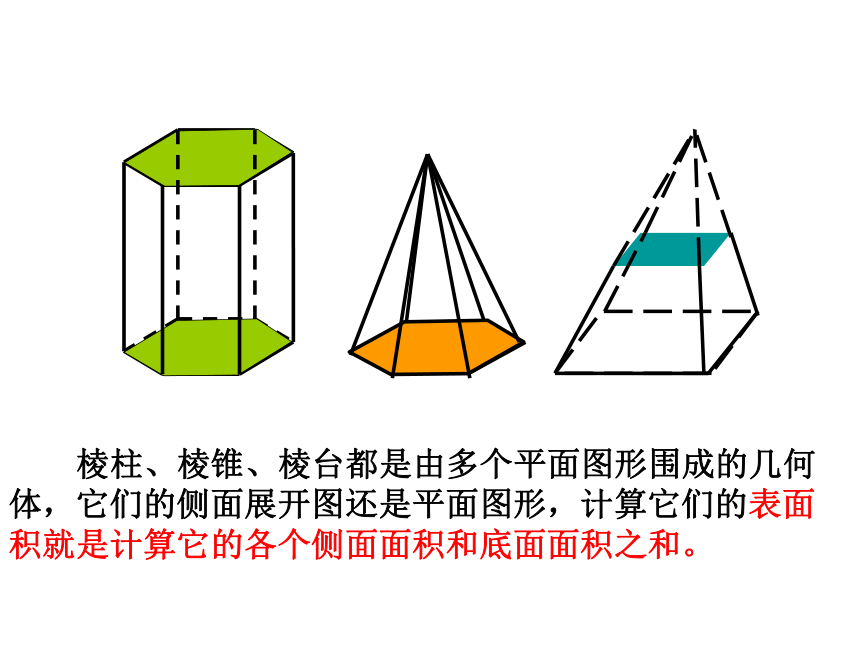
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和。
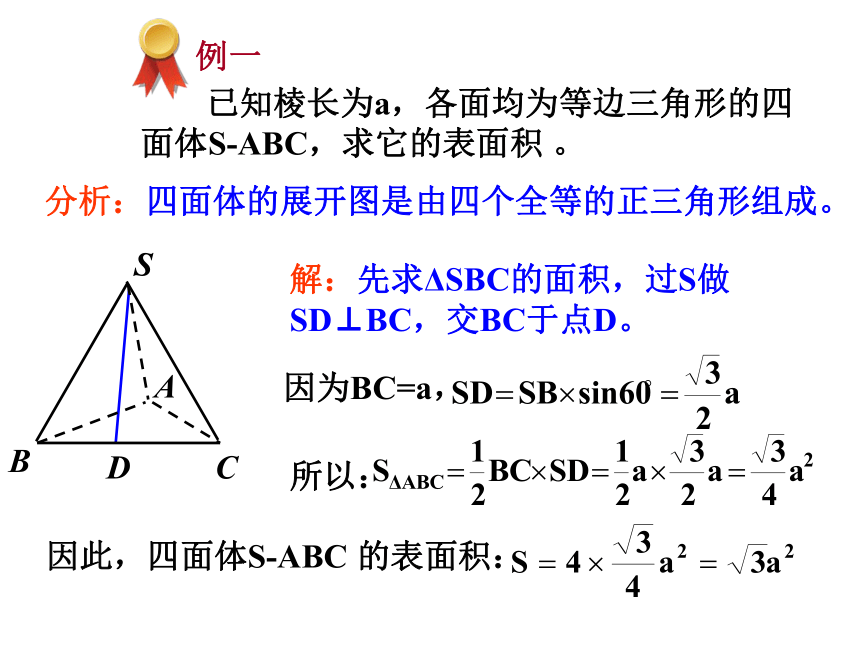
已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积 。
D
B
C
A
S
分析:四面体的展开图是由四个全等的正三角形组成。
因为BC=a,
所以:
因此,四面体S-ABC 的表面积:
解:先求ΔSBC的面积,过S做SD⊥BC,交BC于点D。
例一
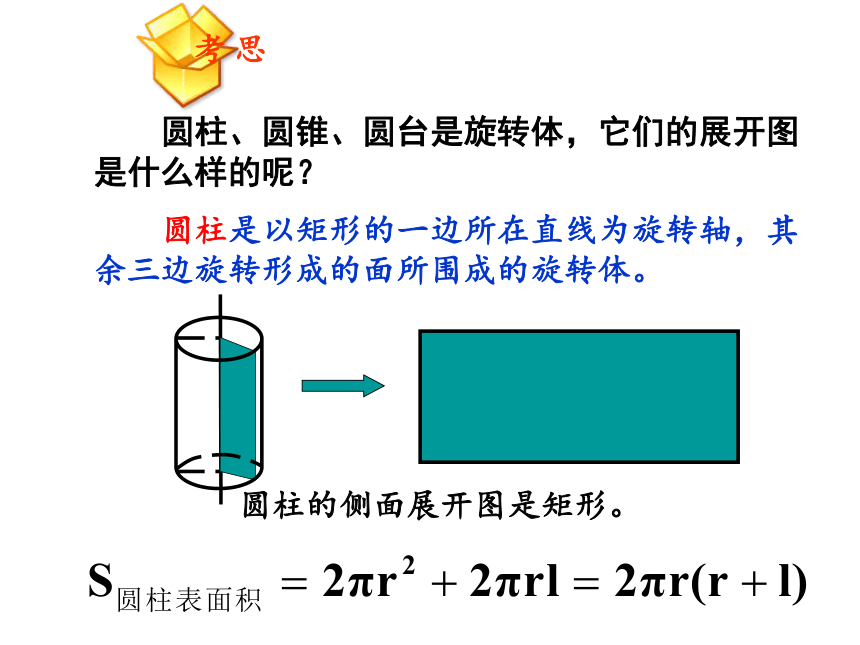
圆柱、圆锥、圆台是旋转体,它们的展开图是什么样的呢?
思考
圆柱是以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体。
圆柱的侧面展开图是矩形。
圆锥是以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体。
圆锥的侧面展开图是扇形。
圆台是以直角梯形的垂直边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体。
圆台的侧面展开图是扇环。
一个圆台形花盆盆口直径20 cm,盆底直径为15cm,底部渗水圆孔直径为1.5 cm,盆壁长15cm。那么花盆的表面积约是多少平方厘米(π取3.14,结果精确到1 cm2 )?
解:由圆台的表面积公式得 花盆的表面积:
答:花盆的表面积约是999 .
例二
r'=r
上底扩大
r'=0
上底缩小
探究
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
2.柱体、椎体、台体的体积
我们已经学习了特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:
(S为底面面积,h为高)
一般柱体体积也是:
其中S为底面面积,h为棱柱的高。
圆锥的体积公式:
(其中S为底面面积,h为高)
棱锥的体积公式:
(其中S为底面面积,h为高)
圆锥体积等于同底等高的圆柱的体积的
棱锥体积等于同底等高的棱柱的体积的
由此可知,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是等于底面面积乘高的 。
探究
如何求台体的体积?
由于圆台(棱台)是由圆锥(棱锥)截成的,因此用两个锥体的体积差。得到圆台(棱台)的体积公式:
其中S,S‘分别为上、下底面面积,h为圆台(棱台)的高。
上底扩大
上底缩小
圆柱、圆锥、圆台三者的体积公式之间有什么关系?
有一堆规格相同的铁制(铁的密是 )六角螺帽共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14)?
例三
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:
所以螺帽的个数为
(个)
答:这堆螺帽大约有252个.
课堂小结
r’=r
上底扩大
r’=0
上底缩小
柱体、椎体、台体的表面积:
上底扩大
上底缩小
柱体、椎体、台体的体积:
课堂小练习
1、一空间几何体的三视图如图所示,则该几何体的体积为( )
俯视图
2
2
2
正(主)视图
2
2
侧(左)视图
A.
B.
C.
D.
C
【解析】:该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为 ,四棱锥的底面边长为 ,高为
所以体积为:
所以该几何体的体积为:
2、设某几何体的三视图(单位:cm)如图所示,(尺寸的长度单位为m).则该几何体的体积为__________。
3
4 m3
正视图
侧视图
俯视图
【解析】由三视图知其为三棱锥,由“主左一样高,主俯一样长,俯左一样宽”可知高为2,地面三角形的底面边长为4,高为3,则所求棱锥体积为:
3、 圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是_______。
4πS
4、 已知圆锥的表面积为 a ㎡,且它的侧面展开图是一个半圆,则这圆锥的底面直径为
______________。
5、 若圆台的上、下底面半径分别是1和3,它的侧面积是两底面积和的2倍,则圆台的母线长为___________.
5
6、 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )
A .
B .
C .
D .
A
7、 已知圆锥的全面积是底面积的3倍,那么这个
圆锥的侧面积展开图-扇形的圆心角为_______度。
180
8、如图,已知:三棱锥A-BCD的侧棱AD垂直于底面
BCD,侧面ABC与底面所成的角为θ。
求证:V三棱锥=?SΔABC·ADcosθ。
证明: 在平面BCD内,作DE⊥BC,垂足为E,连结AE,DE就是AE在平面BCD上的射影。
根据三垂线定理,AE⊥BC。
∴∠AED=θ
V三棱锥=?SΔABC×AD
=?×?×BC×ED×AD
=?×?×BC.AE× cosθ×AD
=?SΔABCADcosθ
A
D
C
E
B
θ
习题答案
1.
2. 1.74千克。
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
导入新课
正方体和长方体是由平面图形围成的多面体,它们表面积就是各个面的面积的和,也就是展开图的面积。
5
4
3
表面积为:4×3×4+4×5×2=88
求多面体表面积的方法:展成平面图形,求面积。
1.3.1 柱体、锥体、台体的
表面积与体积
教学目标
知识与能力
通过对柱、锥、台体的研究,掌握柱、锥、台的表面积和体积的求法。
能运用公式求解柱体、锥体和台体的体积,并且熟悉台体与柱体和锥体之间的转换关系。
过程与方法
让学生经历几何全的侧面展一过程,感知几何体的形状。
让学生通对照比较,了解柱体、锥体、台体的面积和体积的关系。
情感态度与价值观
使学生感受到几何体面积和体积的求解过程,对自己空间思维能力影响 。
教学重难点
柱体、锥体、台体的表面积和体积计算。
台体体积公式的推导。
重点
难点
探究
棱柱、棱锥、棱台的展开图是什么?
棱柱的展开图是平行四边形。
1.柱体、椎体、台体的表面积
棱锥的展开图是三角形。
同理,棱台的展开图呢?
棱台的展开图是梯形。
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和。
已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积 。
D
B
C
A
S
分析:四面体的展开图是由四个全等的正三角形组成。
因为BC=a,
所以:
因此,四面体S-ABC 的表面积:
解:先求ΔSBC的面积,过S做SD⊥BC,交BC于点D。
例一
圆柱、圆锥、圆台是旋转体,它们的展开图是什么样的呢?
思考
圆柱是以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体。
圆柱的侧面展开图是矩形。
圆锥是以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体。
圆锥的侧面展开图是扇形。
圆台是以直角梯形的垂直边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体。
圆台的侧面展开图是扇环。
一个圆台形花盆盆口直径20 cm,盆底直径为15cm,底部渗水圆孔直径为1.5 cm,盆壁长15cm。那么花盆的表面积约是多少平方厘米(π取3.14,结果精确到1 cm2 )?
解:由圆台的表面积公式得 花盆的表面积:
答:花盆的表面积约是999 .
例二
r'=r
上底扩大
r'=0
上底缩小
探究
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
2.柱体、椎体、台体的体积
我们已经学习了特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:
(S为底面面积,h为高)
一般柱体体积也是:
其中S为底面面积,h为棱柱的高。
圆锥的体积公式:
(其中S为底面面积,h为高)
棱锥的体积公式:
(其中S为底面面积,h为高)
圆锥体积等于同底等高的圆柱的体积的
棱锥体积等于同底等高的棱柱的体积的
由此可知,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是等于底面面积乘高的 。
探究
如何求台体的体积?
由于圆台(棱台)是由圆锥(棱锥)截成的,因此用两个锥体的体积差。得到圆台(棱台)的体积公式:
其中S,S‘分别为上、下底面面积,h为圆台(棱台)的高。
上底扩大
上底缩小
圆柱、圆锥、圆台三者的体积公式之间有什么关系?
有一堆规格相同的铁制(铁的密是 )六角螺帽共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14)?
例三
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:
所以螺帽的个数为
(个)
答:这堆螺帽大约有252个.
课堂小结
r’=r
上底扩大
r’=0
上底缩小
柱体、椎体、台体的表面积:
上底扩大
上底缩小
柱体、椎体、台体的体积:
课堂小练习
1、一空间几何体的三视图如图所示,则该几何体的体积为( )
俯视图
2
2
2
正(主)视图
2
2
侧(左)视图
A.
B.
C.
D.
C
【解析】:该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为 ,四棱锥的底面边长为 ,高为
所以体积为:
所以该几何体的体积为:
2、设某几何体的三视图(单位:cm)如图所示,(尺寸的长度单位为m).则该几何体的体积为__________。
3
4 m3
正视图
侧视图
俯视图
【解析】由三视图知其为三棱锥,由“主左一样高,主俯一样长,俯左一样宽”可知高为2,地面三角形的底面边长为4,高为3,则所求棱锥体积为:
3、 圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是_______。
4πS
4、 已知圆锥的表面积为 a ㎡,且它的侧面展开图是一个半圆,则这圆锥的底面直径为
______________。
5、 若圆台的上、下底面半径分别是1和3,它的侧面积是两底面积和的2倍,则圆台的母线长为___________.
5
6、 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )
A .
B .
C .
D .
A
7、 已知圆锥的全面积是底面积的3倍,那么这个
圆锥的侧面积展开图-扇形的圆心角为_______度。
180
8、如图,已知:三棱锥A-BCD的侧棱AD垂直于底面
BCD,侧面ABC与底面所成的角为θ。
求证:V三棱锥=?SΔABC·ADcosθ。
证明: 在平面BCD内,作DE⊥BC,垂足为E,连结AE,DE就是AE在平面BCD上的射影。
根据三垂线定理,AE⊥BC。
∴∠AED=θ
V三棱锥=?SΔABC×AD
=?×?×BC×ED×AD
=?×?×BC.AE× cosθ×AD
=?SΔABCADcosθ
A
D
C
E
B
θ
习题答案
1.
2. 1.74千克。
