必修2 高二数学 2.2.4平面与平面平行的性质 上课课件(共23张PPT)
文档属性
| 名称 | 必修2 高二数学 2.2.4平面与平面平行的性质 上课课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 469.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
新课导入
如果两个平面平行,那么一平面中的直线与另一平面有什么位置关系?
如果两个平面平行,那么一个平面内的直线与另一个平面的直线具有什么位置关系?
教学目标
知识与能力
掌握两个平面平行的性质定理及其应用。
过程与方法
学生通过观察与类比,借助实物模型理解性质及应用。
情感态度与价值观
进一步提高学生空间想象能力、思维能力。
进一步体会类比的作用。
进一步渗透等价转化的思想。
教学重难点
重点
难点
性质定理
判定定理
性质定理的证明
性质定理的正确运用
2.2.4 平面与平面平行的性质
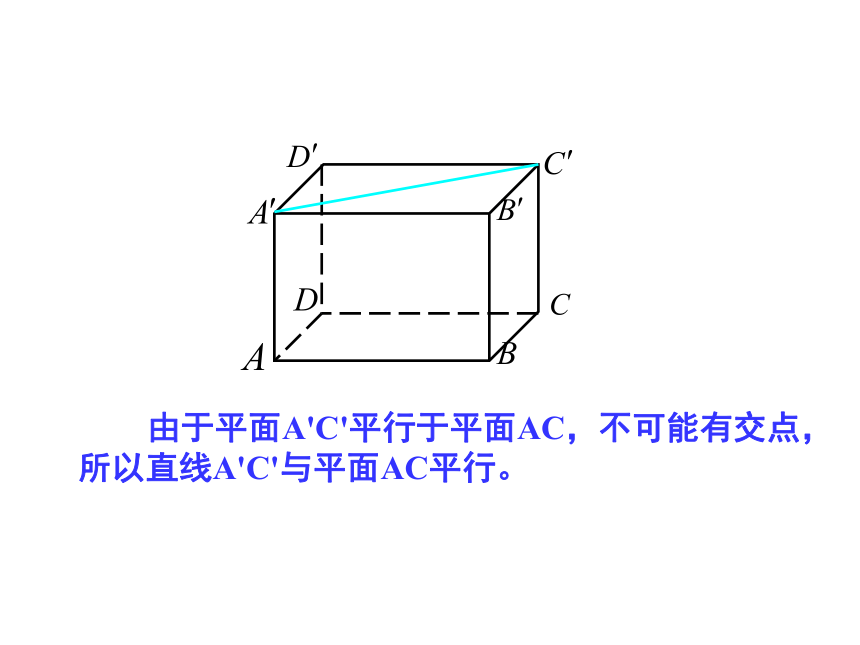
在上图中,直线A'C'所在平面A'C'与平面AC平行,那直线A'C'与平面AC是什么位置关系呢?
探究
(1)如果两个平面平行,那么一平面中的直线与另一平面有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC平行。
在左图中,直线A'C'与平面AC中的直线都有什么位置关系呢?
(2)如果两个平面平行,那么一平面中的直线与另一平面内的直线都有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC内直线的位置关系只可能是平行或异面.如A'C'与AC平行,与AB或BC异面。
(3)如何找到在平面AC中与直线A'C'平行的直线?
只要与直线A'C'在一个平面内即可.过直线A'C'做一个平面与平面AC相交,则交线与直线A'C'平行。
1. 若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2. 平行于同一平面的两平面平行;
3. 过平面外一点有且只有一个平面与这个平面平行;
4. 夹在两平行平面间的平行线段相等。
(4)由两个平面平行可以得到哪些既然论呢?
例七
a
b
α
β
γ
如图,已知平面α,β,γ,满足α//β,α∩γ=a,β∩γ=b,求证:a//b。
证明:
所以a,b没有公共点
平面和平面平行的性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
符号表示:
面面平行 线线平行
证明:因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交AC和BD
因为α//β,
所以BD//AC
因此,四边形ABCD是平行四边形
所以AB=CD
例六
A
C
B
D
已知:如图α//β,AB//CD,且
求证:AB=CD
求证:夹在两个平行平面同时和第三个平面相交,那么它们的交线平行。
课堂小结
面面平行判定定理:
线面平行 面面平行
面面平行性质定理:
面面平行 线面平行
线面平行判定定理:
线线平行 线面平行
线面平行性质定理:
线面平行 线面平行
转化思想:
直线与平面平行的判定定理可以判定线面平行。
直线与平面平行的性质定理可以得出线线平行。
平面与平面平行的判定定理可以判定面面平行。
平面与平面平行的性质定理可以得出线面平行、线线平行。
1.已知α∥β,AB交α、β于A、B,CD交α、β于C、D,AB∩CD=S,AS=8,BS=9,CD=34,求SC。
α
β
A
D
C
B
S
α
β
C
B
S
A
D
课堂过关小练习
A1
B1
C1
D1
A
B
C
D
2.已知P、Q是边长为1的正方体ABCD-A1B1C1D1的面AA1DD1 、面ABCD的中心。
(1)求证:PQ// 平面DD1C1C
(2)求线段的PQ长.
P
Q
3. 、β、γ为三个不重合的平面,a,b,c为三条不同直线,则有一下列命题,不正确的是
①
③
⑤
⑥
②
④
a∥cb∥c
a∥b
a∥γb∥γ
a∥b
a∥c
β∥c
a∥β
a∥γ
β∥γ
a∥β
a∥c
∥c
∥a
a∥γ
∥γ
a∥
②③⑥
4.如图,已知AB、CD是夹在两个平行平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面β。
A
B
C
D
α
M
N
β
E
l
5.在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线B′M与平面A′BD的位置关系,并说明理由。
A′
B′
C′
D′
A
B
C
D
M
新课导入
如果两个平面平行,那么一平面中的直线与另一平面有什么位置关系?
如果两个平面平行,那么一个平面内的直线与另一个平面的直线具有什么位置关系?
教学目标
知识与能力
掌握两个平面平行的性质定理及其应用。
过程与方法
学生通过观察与类比,借助实物模型理解性质及应用。
情感态度与价值观
进一步提高学生空间想象能力、思维能力。
进一步体会类比的作用。
进一步渗透等价转化的思想。
教学重难点
重点
难点
性质定理
判定定理
性质定理的证明
性质定理的正确运用
2.2.4 平面与平面平行的性质
在上图中,直线A'C'所在平面A'C'与平面AC平行,那直线A'C'与平面AC是什么位置关系呢?
探究
(1)如果两个平面平行,那么一平面中的直线与另一平面有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC平行。
在左图中,直线A'C'与平面AC中的直线都有什么位置关系呢?
(2)如果两个平面平行,那么一平面中的直线与另一平面内的直线都有什么位置关系?
由于平面A'C'平行于平面AC,不可能有交点,所以直线A'C'与平面AC内直线的位置关系只可能是平行或异面.如A'C'与AC平行,与AB或BC异面。
(3)如何找到在平面AC中与直线A'C'平行的直线?
只要与直线A'C'在一个平面内即可.过直线A'C'做一个平面与平面AC相交,则交线与直线A'C'平行。
1. 若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2. 平行于同一平面的两平面平行;
3. 过平面外一点有且只有一个平面与这个平面平行;
4. 夹在两平行平面间的平行线段相等。
(4)由两个平面平行可以得到哪些既然论呢?
例七
a
b
α
β
γ
如图,已知平面α,β,γ,满足α//β,α∩γ=a,β∩γ=b,求证:a//b。
证明:
所以a,b没有公共点
平面和平面平行的性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
符号表示:
面面平行 线线平行
证明:因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交AC和BD
因为α//β,
所以BD//AC
因此,四边形ABCD是平行四边形
所以AB=CD
例六
A
C
B
D
已知:如图α//β,AB//CD,且
求证:AB=CD
求证:夹在两个平行平面同时和第三个平面相交,那么它们的交线平行。
课堂小结
面面平行判定定理:
线面平行 面面平行
面面平行性质定理:
面面平行 线面平行
线面平行判定定理:
线线平行 线面平行
线面平行性质定理:
线面平行 线面平行
转化思想:
直线与平面平行的判定定理可以判定线面平行。
直线与平面平行的性质定理可以得出线线平行。
平面与平面平行的判定定理可以判定面面平行。
平面与平面平行的性质定理可以得出线面平行、线线平行。
1.已知α∥β,AB交α、β于A、B,CD交α、β于C、D,AB∩CD=S,AS=8,BS=9,CD=34,求SC。
α
β
A
D
C
B
S
α
β
C
B
S
A
D
课堂过关小练习
A1
B1
C1
D1
A
B
C
D
2.已知P、Q是边长为1的正方体ABCD-A1B1C1D1的面AA1DD1 、面ABCD的中心。
(1)求证:PQ// 平面DD1C1C
(2)求线段的PQ长.
P
Q
3. 、β、γ为三个不重合的平面,a,b,c为三条不同直线,则有一下列命题,不正确的是
①
③
⑤
⑥
②
④
a∥cb∥c
a∥b
a∥γb∥γ
a∥b
a∥c
β∥c
a∥β
a∥γ
β∥γ
a∥β
a∥c
∥c
∥a
a∥γ
∥γ
a∥
②③⑥
4.如图,已知AB、CD是夹在两个平行平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面β。
A
B
C
D
α
M
N
β
E
l
5.在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线B′M与平面A′BD的位置关系,并说明理由。
A′
B′
C′
D′
A
B
C
D
M
