5.2 平抛运动的应用—有约束条件的平抛运动 (68张PPT)
文档属性
| 名称 | 5.2 平抛运动的应用—有约束条件的平抛运动 (68张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览









文档简介
(共68张PPT)
专题:
平抛运动中的典型问题
1、承接面:平面;斜面;曲面。
2、临界问题。
3、反射问题。
4、假设法应用问题。
典型问题一:
平面上的平抛问题
例1
例2
例3
例4
典型问题一:
斜面上的平抛问题
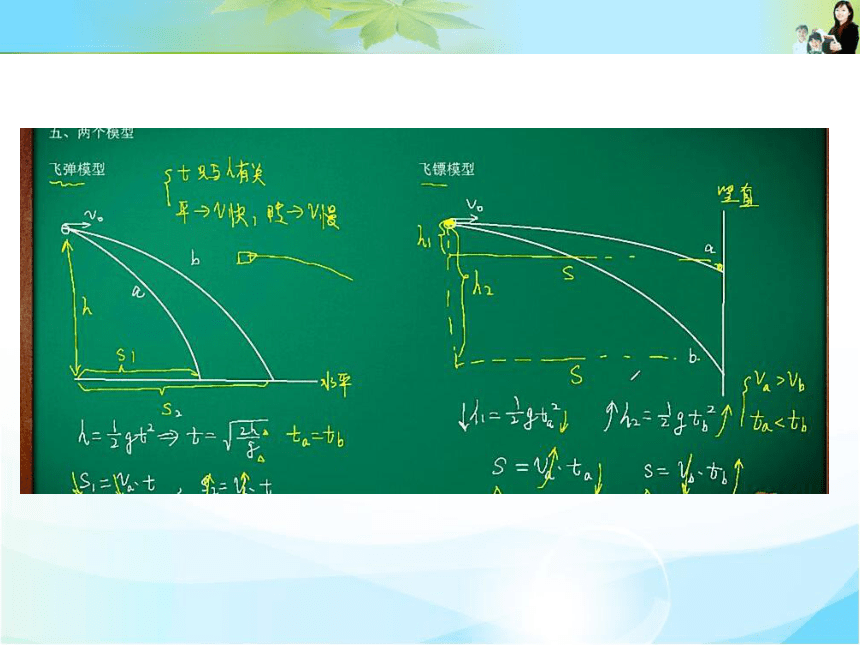
模型阐述:
平抛运动与斜面相结合的模型,其特点是做平抛运动的物体落在斜面上,包括两种情况:
(1)从斜面上抛出落到斜面上
(2)从空中抛出落到斜面上
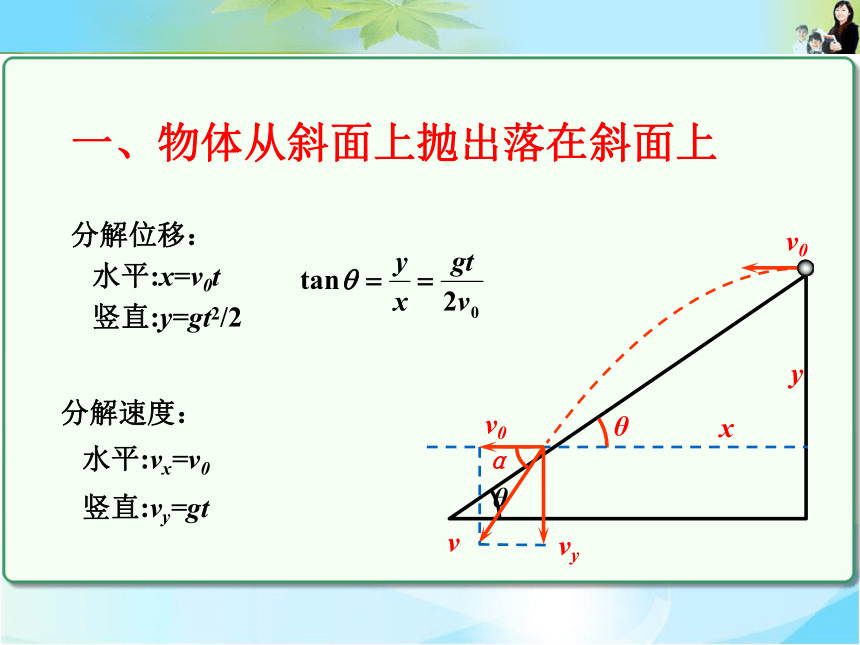
一、物体从斜面上抛出落在斜面上
分解位移:
水平:x=v0t
竖直:y=gt2/2
θ
v0
θ
x
y
α
v
v0
vy
分解速度:
水平:vx=v0
竖直:vy=gt
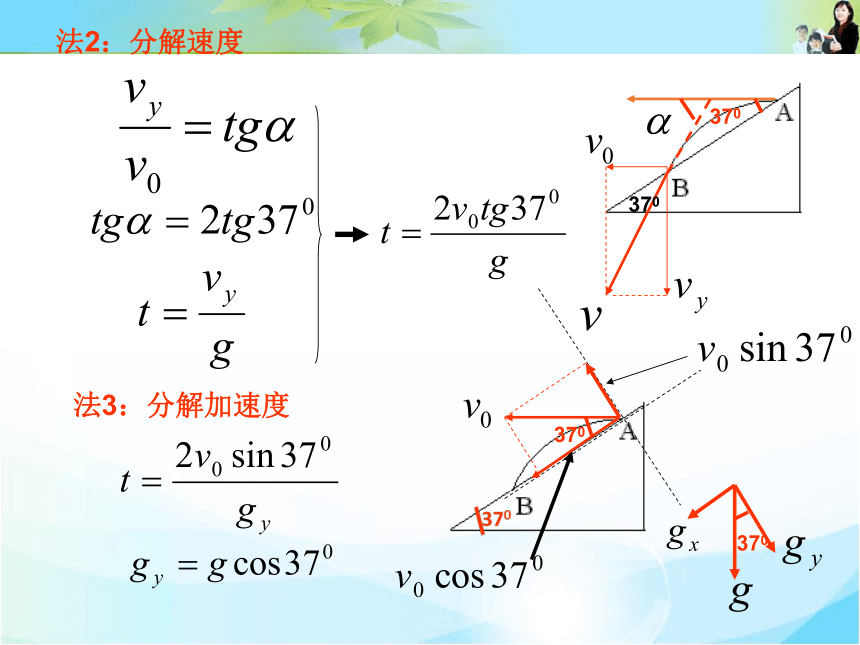
【例1】如图所示,在与水平方向成37°角的斜坡上的A点,以10m/s的速度水平抛出一个小球,求落在斜坡上的B点与A点的距离及在空中飞行的时间?
法1:
分解位移
法2:分解速度
370
370
法3:分解加速度
370
370
斜面上的平抛运动的分析方法
反思总结
在斜面上以不同的初速度水平抛出的物体,若落点仍在斜面上,则存在以下规律:
(1)物体的竖直位移与水平位移之比是同一个常数,这个常数等于斜面倾角的正切值;
(2)运动时间与初速度成正比;位移与初速度的平方成正比
(3)物体落在斜面上,位移方向相同,都沿斜面方向;
(4)物体落在斜面上时的速度方向平行;
(5)当物体的速度方向与斜面平行时,物体离斜面的距离最远;时间为总时间的一半。
二、物体从空中抛出落在斜面上
分解速度:水平:vx=v0
竖直:vy=gt
tanθ=vx/vy=v0/gt
θ
x
y
v0
θ
v
v0
vy
情况1:速度垂直斜面
分解位移:
水平:x=v0t
竖直:y=gt2/2
方法指导:充分利用斜面倾角,找出斜面倾角同位移和速度的关系,从而使问题得到顺利解决。
【例2】如图示,轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h,山坡倾角为θ,由此可算出( ).
A.轰炸机的飞行高度
B.轰炸机的飞行速度
C.炸弹的飞行时间
D.炸弹投出时的动能
审题设疑
1、审题中的关键着眼点在哪里?
2、通过什么办法找出各量之间的关系,列方程求解?
H
x
θ
v
v0
vy
ABC
转原题
答案
解析
例1
小球到斜面的最小位移如图所示.
小球运动轨迹及分运动位移
D
θ
典型问题一:
曲面上的平抛问题
例1
答案
解析
解析
典型问题二
平抛运动的临界问题
【例6】如图,排球场总长18m,设网的高度为2m,运动员站在离网3m远的线上正对网前竖直跳起把球水平击出.(g=10m/s2).
(1)设击球点的高度为2.5m,问球被水平击出时的速度在什么范围内才能使球既不触网也不出界?
(2)若击球点的高度小于某个值,那么无论球被水平击出的速度多大,球不是触网就是出界,试求此高度?
设球刚好打在边界上,
水平位移: x2=12m,球下落高度: h2 = 2.5m
此时水平位移: x1=3m,
球下落高度:△h= h2-h1 = 2.5-2.0 = 0.5m
(1)设球刚好擦网而过,
使球既不触网也不出界,则球的速度应满足:
设击球点高度为h3时,球恰好既触网又压线。再设此时排球飞出的初速度为v0,
球刚好触网, 水平方向: x3=3m ,
竖直方向为:△h1=h3-h1
对于刚好压线:水平方向:x4=12m,竖直方向为:h3
(2)若击球点的高度为何值时,那么无论球被水平击出的速度多大,球不是触网就是出界,试求此高度?
例1
答案
解析
典型问题三
遵从反射定律的问题
【例8】.如图所示,平行竖直的两块钢板高为H,相距S,从左上角A点垂直于板水平抛出一小球,球在B、C两处与板做弹性碰撞(碰撞前后速率大小不变,方向改变)后落在两块钢板的正中间的D点,则A与B点、B与C点、C与D点的高度差h1、 h2 、 h3 之比为------------------。
解析:小球与板碰撞后的轨迹,相当于将抛物线对称到竖直线的另一侧,由自由落体运动的特点,将整个时间分成相等的5 段,得
解.(1)落到抛出点正下方应满足:
2kd=v0 t y=h
得到;
同理:落到左板正下方满足
(2k+1)d= y=h
得到:
典型问题四
假设法应用问题
例1
典型问题五
类平抛运动问题
一、物体做类平抛运动的条件
如果一个物体受到与初速度方向垂直的恒定的合外力作用而做的曲线运动,即类平抛运动。
二、类平抛运动的规律与平抛运动类似,轨迹仍然是抛物线
四、类平抛运动的分解
分运动一:沿初速度的方向做匀速直线运动;
分运动二:垂直于初速度方向的初速度为0的匀加速直线运动。
例1、光滑水平面上,一个质量为0.5千克的物体从静止开始在前5秒内受一个正东方向,大小为1N的水平恒力作用而运动;第5秒末撤去该力,改受一个正北方向,大小为0.5N的水平恒力,作用时间为10秒(忽略重力)。
求:(1)该物体在前5秒和后10秒各做什么运动?
(2)第15秒末速度大小和方向?
(g=10m/S2)
北
东
F1=1N
F2=0.5N
V
解:(1)前5秒做初速度为零的匀加速直线运动;
后10秒做东偏北的类平抛运动。
(2)
θ
例2、如图,光滑斜面长为a,宽为b,倾角为θ,一个物体从斜面上方左端顶点P水平射入,恰能从右下方端点Q离开斜面,试求入射的初速度V0?
θ
V0
P
a
b
Q
例3、A、B两质点以相同的水平速度在坐标原点O沿X轴正方向抛出,A在竖直平面内运动,落地点为P1,B沿光滑斜面运动,落地点为P2,P1、P2对应的X轴坐标分别为X1和X2,不计空气阻力,下列说法正确的是:( )
A、X1>X2 B、X1C、X1=X2 D、A先到达P1点
θ
h
X
P2
P1
O
BD
冲淡重力
答案
例3
解析
典型问题六
斜抛运动问题
2019.9.29 高一新生自制水火箭
将物体以一定的初速度沿斜上方抛出,仅在重力作用下的运动叫做斜抛运动。
3、概念:
1、条件:
⑴、物体有斜向上的初速度。
⑵、仅受重力作用
2、轨迹特点:
曲线
什么是斜抛运动?
注意:任何时刻速度方向与受力方向都不可能共线
一、问题
v0
G
二、探究
斜抛运动的律?
x
水平方向初速度: Vox = Vo cos ?, ax = 0
竖直方向初速度: Voy = Vo sin ?, ay = g,方向向下
水平方向:匀速直线运动
竖直方向:竖直上抛运动
?
y
vox
voy
vo
射高H
射程S
四、斜抛运动的规律:
位移: x=voxt= v0t cosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度 :vx =v0x =v0 cosθ
水平方向:
匀速直线运动
竖直方向:
竖直上抛运动
X轴:
Y轴:
规律
v0y
v0
x
v0x
y
0
v
vx
vy
一.速度
大小:
方向:
二位移
大小:
S
y
x
方向:
分
解
=
射高:
射程:
飞行时间:
2、怎样计算射程、射高和飞行时间?
探究射高和射程与初速度和抛射角的关系:
(1)探究射高h和射程s与初速度的关系
在抛射角不变的情况下,水流的初速度增大,射程________, 射高_________
(2)探究射高h和射程s与抛射角的关系
控制流量最大,初速度一样,改变抛射角度(30°、45 °、60 °、90 °),
①抛射角<45°,抛射角增大,射程_____,射高_____
②抛射角=45°, 射程_____,射高_____
③抛射角>45°,抛射角增大,射程_____,射高_____
④抛射角=90°, 射程 ,射高_____
增大
增大
增大
最大
减小
增大
最大
最小=0
增大
增大
推铅球时铅球的抛出点与落地点不在同一水平面上,而是有一定高度差,所以最远射程并不发生在抛射角450 时,而是要小一些,大约为为420左右。
1、以初速度Vo,抛射角?向斜上方抛出一个物体,由抛出到经过
最高点的时间是 ,经过最高点的速度是 。
2、做斜上抛运动的物体,在2s末经过最高点时的速度是15m/s,
g=10m/s2,则初速度Vo= m/s,抛射角?= o。
V o sin ?
g
Vo cos ?
ty =
V o sin ?
g
Vx=Vo cos ?=15
ty =
V o sin ?
g
=2
Vo=25(m/s), ?=53o
25
53
反馈练习
扔铅球
六.弹道曲线
——作斜抛运动的炮弹(物体)在空气中飞行的实际轨迹,称为弹道曲线。
注意: 1.弹道曲线的升弧和降弧不再对称。
——升弧长而平伸,降弧短而弯曲。
2.弹道曲线形成的原因主要是空气阻力。
——空气阻力影响的程度与抛体本身的形状和质量、
空气的密度、 抛体的速率等因素有关。
物体的初速度很大时(如射出的枪弹、炮弹等),空气阻力的影响是很大的,轨迹不再是理论上的抛物线,这种实际的抛体运动曲线通常称为弹道曲线。
下一张
上一张
Ⅰ:v<200m/s时,f∝v2;
Ⅱ:400m/s<v<600m/s
时,f∝v3;
Ⅲ:v>600m/s
时,f∝vn;
⑴、低速迫击炮理想射程360米,实际是350米;
⑵、加农炮理想射程46km,实际13km;
举例:
巩固练习
1、在斜抛运动中,飞行时间由什么物理量来决定?水平射程呢?
2、斜上抛的物体在最高点时下列哪个物理量为零?
A 速度
B 水平分速度
C 竖直分速度
D 加速度
下一张
上一张
3、把物体沿某一方向抛出后,在相等时间内(在空中),下列哪些物理量相等(空气阻力不计)
A、加速度
B、位移
C、速度变化量
D、水平方向位移
A、C、 D
解:(1)斜抛物体经ts后在x、y的方向的分速度为:
当t=1s 时,速度与水平方向成
即:
(2)达到最高点时时:
即:
练习4:斜向上抛出一球,抛射角 ,当t=1s时,球仍斜向上升,但方向与跟水平方向成 角,(1)球的初速度 是多少?(2)球将在什么时候达到最高点?( )
5、一足球运动员开出角球,球的初速度是20m/s,初速度方向跟水平面的夹角是53°。如果球在飞行过程中,没有被任何一名队员碰到,空气阻力不计,g取10m/s2,求
斜抛运动
G
v0
y
o
vx
vy
θ
(1)落点与开出点之间的距离
(2)球在运行过程中,球离地面的最大距离。
x
P
1.斜抛运动是匀变速运动;
2.处理方法:分解运动
小结:
1、斜抛运动
2、斜抛运动分解为
水平方向:
匀速直线运动
竖直方向:
竖直上抛运动
X轴:
Y轴:
3、斜抛运动的规律:先分解再合成
位移: x=voxt= v0t cosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度 :vx =v0x =v0 cosθ
水平方向:
竖直方向:
速度
大小:
方向:
位移
大小:
方向:
4、斜抛运动的射程与射高
射程
射高
射程随初速度增大而增大
射程与抛射角有关,当抛射角为450时射程最大,(实际
由于空气阻力作用,抛射角为420左右)
初速度越大射高就越大,当抛射角为900时射高最大
作业(书面)P62 1——3,P63 4
练习册
专题:
平抛运动中的典型问题
1、承接面:平面;斜面;曲面。
2、临界问题。
3、反射问题。
4、假设法应用问题。
典型问题一:
平面上的平抛问题
例1
例2
例3
例4
典型问题一:
斜面上的平抛问题
模型阐述:
平抛运动与斜面相结合的模型,其特点是做平抛运动的物体落在斜面上,包括两种情况:
(1)从斜面上抛出落到斜面上
(2)从空中抛出落到斜面上
一、物体从斜面上抛出落在斜面上
分解位移:
水平:x=v0t
竖直:y=gt2/2
θ
v0
θ
x
y
α
v
v0
vy
分解速度:
水平:vx=v0
竖直:vy=gt
【例1】如图所示,在与水平方向成37°角的斜坡上的A点,以10m/s的速度水平抛出一个小球,求落在斜坡上的B点与A点的距离及在空中飞行的时间?
法1:
分解位移
法2:分解速度
370
370
法3:分解加速度
370
370
斜面上的平抛运动的分析方法
反思总结
在斜面上以不同的初速度水平抛出的物体,若落点仍在斜面上,则存在以下规律:
(1)物体的竖直位移与水平位移之比是同一个常数,这个常数等于斜面倾角的正切值;
(2)运动时间与初速度成正比;位移与初速度的平方成正比
(3)物体落在斜面上,位移方向相同,都沿斜面方向;
(4)物体落在斜面上时的速度方向平行;
(5)当物体的速度方向与斜面平行时,物体离斜面的距离最远;时间为总时间的一半。
二、物体从空中抛出落在斜面上
分解速度:水平:vx=v0
竖直:vy=gt
tanθ=vx/vy=v0/gt
θ
x
y
v0
θ
v
v0
vy
情况1:速度垂直斜面
分解位移:
水平:x=v0t
竖直:y=gt2/2
方法指导:充分利用斜面倾角,找出斜面倾角同位移和速度的关系,从而使问题得到顺利解决。
【例2】如图示,轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h,山坡倾角为θ,由此可算出( ).
A.轰炸机的飞行高度
B.轰炸机的飞行速度
C.炸弹的飞行时间
D.炸弹投出时的动能
审题设疑
1、审题中的关键着眼点在哪里?
2、通过什么办法找出各量之间的关系,列方程求解?
H
x
θ
v
v0
vy
ABC
转原题
答案
解析
例1
小球到斜面的最小位移如图所示.
小球运动轨迹及分运动位移
D
θ
典型问题一:
曲面上的平抛问题
例1
答案
解析
解析
典型问题二
平抛运动的临界问题
【例6】如图,排球场总长18m,设网的高度为2m,运动员站在离网3m远的线上正对网前竖直跳起把球水平击出.(g=10m/s2).
(1)设击球点的高度为2.5m,问球被水平击出时的速度在什么范围内才能使球既不触网也不出界?
(2)若击球点的高度小于某个值,那么无论球被水平击出的速度多大,球不是触网就是出界,试求此高度?
设球刚好打在边界上,
水平位移: x2=12m,球下落高度: h2 = 2.5m
此时水平位移: x1=3m,
球下落高度:△h= h2-h1 = 2.5-2.0 = 0.5m
(1)设球刚好擦网而过,
使球既不触网也不出界,则球的速度应满足:
设击球点高度为h3时,球恰好既触网又压线。再设此时排球飞出的初速度为v0,
球刚好触网, 水平方向: x3=3m ,
竖直方向为:△h1=h3-h1
对于刚好压线:水平方向:x4=12m,竖直方向为:h3
(2)若击球点的高度为何值时,那么无论球被水平击出的速度多大,球不是触网就是出界,试求此高度?
例1
答案
解析
典型问题三
遵从反射定律的问题
【例8】.如图所示,平行竖直的两块钢板高为H,相距S,从左上角A点垂直于板水平抛出一小球,球在B、C两处与板做弹性碰撞(碰撞前后速率大小不变,方向改变)后落在两块钢板的正中间的D点,则A与B点、B与C点、C与D点的高度差h1、 h2 、 h3 之比为------------------。
解析:小球与板碰撞后的轨迹,相当于将抛物线对称到竖直线的另一侧,由自由落体运动的特点,将整个时间分成相等的5 段,得
解.(1)落到抛出点正下方应满足:
2kd=v0 t y=h
得到;
同理:落到左板正下方满足
(2k+1)d= y=h
得到:
典型问题四
假设法应用问题
例1
典型问题五
类平抛运动问题
一、物体做类平抛运动的条件
如果一个物体受到与初速度方向垂直的恒定的合外力作用而做的曲线运动,即类平抛运动。
二、类平抛运动的规律与平抛运动类似,轨迹仍然是抛物线
四、类平抛运动的分解
分运动一:沿初速度的方向做匀速直线运动;
分运动二:垂直于初速度方向的初速度为0的匀加速直线运动。
例1、光滑水平面上,一个质量为0.5千克的物体从静止开始在前5秒内受一个正东方向,大小为1N的水平恒力作用而运动;第5秒末撤去该力,改受一个正北方向,大小为0.5N的水平恒力,作用时间为10秒(忽略重力)。
求:(1)该物体在前5秒和后10秒各做什么运动?
(2)第15秒末速度大小和方向?
(g=10m/S2)
北
东
F1=1N
F2=0.5N
V
解:(1)前5秒做初速度为零的匀加速直线运动;
后10秒做东偏北的类平抛运动。
(2)
θ
例2、如图,光滑斜面长为a,宽为b,倾角为θ,一个物体从斜面上方左端顶点P水平射入,恰能从右下方端点Q离开斜面,试求入射的初速度V0?
θ
V0
P
a
b
Q
例3、A、B两质点以相同的水平速度在坐标原点O沿X轴正方向抛出,A在竖直平面内运动,落地点为P1,B沿光滑斜面运动,落地点为P2,P1、P2对应的X轴坐标分别为X1和X2,不计空气阻力,下列说法正确的是:( )
A、X1>X2 B、X1
θ
h
X
P2
P1
O
BD
冲淡重力
答案
例3
解析
典型问题六
斜抛运动问题
2019.9.29 高一新生自制水火箭
将物体以一定的初速度沿斜上方抛出,仅在重力作用下的运动叫做斜抛运动。
3、概念:
1、条件:
⑴、物体有斜向上的初速度。
⑵、仅受重力作用
2、轨迹特点:
曲线
什么是斜抛运动?
注意:任何时刻速度方向与受力方向都不可能共线
一、问题
v0
G
二、探究
斜抛运动的律?
x
水平方向初速度: Vox = Vo cos ?, ax = 0
竖直方向初速度: Voy = Vo sin ?, ay = g,方向向下
水平方向:匀速直线运动
竖直方向:竖直上抛运动
?
y
vox
voy
vo
射高H
射程S
四、斜抛运动的规律:
位移: x=voxt= v0t cosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度 :vx =v0x =v0 cosθ
水平方向:
匀速直线运动
竖直方向:
竖直上抛运动
X轴:
Y轴:
规律
v0y
v0
x
v0x
y
0
v
vx
vy
一.速度
大小:
方向:
二位移
大小:
S
y
x
方向:
分
解
=
射高:
射程:
飞行时间:
2、怎样计算射程、射高和飞行时间?
探究射高和射程与初速度和抛射角的关系:
(1)探究射高h和射程s与初速度的关系
在抛射角不变的情况下,水流的初速度增大,射程________, 射高_________
(2)探究射高h和射程s与抛射角的关系
控制流量最大,初速度一样,改变抛射角度(30°、45 °、60 °、90 °),
①抛射角<45°,抛射角增大,射程_____,射高_____
②抛射角=45°, 射程_____,射高_____
③抛射角>45°,抛射角增大,射程_____,射高_____
④抛射角=90°, 射程 ,射高_____
增大
增大
增大
最大
减小
增大
最大
最小=0
增大
增大
推铅球时铅球的抛出点与落地点不在同一水平面上,而是有一定高度差,所以最远射程并不发生在抛射角450 时,而是要小一些,大约为为420左右。
1、以初速度Vo,抛射角?向斜上方抛出一个物体,由抛出到经过
最高点的时间是 ,经过最高点的速度是 。
2、做斜上抛运动的物体,在2s末经过最高点时的速度是15m/s,
g=10m/s2,则初速度Vo= m/s,抛射角?= o。
V o sin ?
g
Vo cos ?
ty =
V o sin ?
g
Vx=Vo cos ?=15
ty =
V o sin ?
g
=2
Vo=25(m/s), ?=53o
25
53
反馈练习
扔铅球
六.弹道曲线
——作斜抛运动的炮弹(物体)在空气中飞行的实际轨迹,称为弹道曲线。
注意: 1.弹道曲线的升弧和降弧不再对称。
——升弧长而平伸,降弧短而弯曲。
2.弹道曲线形成的原因主要是空气阻力。
——空气阻力影响的程度与抛体本身的形状和质量、
空气的密度、 抛体的速率等因素有关。
物体的初速度很大时(如射出的枪弹、炮弹等),空气阻力的影响是很大的,轨迹不再是理论上的抛物线,这种实际的抛体运动曲线通常称为弹道曲线。
下一张
上一张
Ⅰ:v<200m/s时,f∝v2;
Ⅱ:400m/s<v<600m/s
时,f∝v3;
Ⅲ:v>600m/s
时,f∝vn;
⑴、低速迫击炮理想射程360米,实际是350米;
⑵、加农炮理想射程46km,实际13km;
举例:
巩固练习
1、在斜抛运动中,飞行时间由什么物理量来决定?水平射程呢?
2、斜上抛的物体在最高点时下列哪个物理量为零?
A 速度
B 水平分速度
C 竖直分速度
D 加速度
下一张
上一张
3、把物体沿某一方向抛出后,在相等时间内(在空中),下列哪些物理量相等(空气阻力不计)
A、加速度
B、位移
C、速度变化量
D、水平方向位移
A、C、 D
解:(1)斜抛物体经ts后在x、y的方向的分速度为:
当t=1s 时,速度与水平方向成
即:
(2)达到最高点时时:
即:
练习4:斜向上抛出一球,抛射角 ,当t=1s时,球仍斜向上升,但方向与跟水平方向成 角,(1)球的初速度 是多少?(2)球将在什么时候达到最高点?( )
5、一足球运动员开出角球,球的初速度是20m/s,初速度方向跟水平面的夹角是53°。如果球在飞行过程中,没有被任何一名队员碰到,空气阻力不计,g取10m/s2,求
斜抛运动
G
v0
y
o
vx
vy
θ
(1)落点与开出点之间的距离
(2)球在运行过程中,球离地面的最大距离。
x
P
1.斜抛运动是匀变速运动;
2.处理方法:分解运动
小结:
1、斜抛运动
2、斜抛运动分解为
水平方向:
匀速直线运动
竖直方向:
竖直上抛运动
X轴:
Y轴:
3、斜抛运动的规律:先分解再合成
位移: x=voxt= v0t cosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度 :vx =v0x =v0 cosθ
水平方向:
竖直方向:
速度
大小:
方向:
位移
大小:
方向:
4、斜抛运动的射程与射高
射程
射高
射程随初速度增大而增大
射程与抛射角有关,当抛射角为450时射程最大,(实际
由于空气阻力作用,抛射角为420左右)
初速度越大射高就越大,当抛射角为900时射高最大
作业(书面)P62 1——3,P63 4
练习册
