五年级下册数学学案- 2.2 数轴-沪教版(无答案)
文档属性
| 名称 | 五年级下册数学学案- 2.2 数轴-沪教版(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 68.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 21:34:55 | ||
图片预览

文档简介
数轴
【学习目标】
1.通过与温度计的类比认识数轴,能正确画出数轴;
2.能用数轴上点表示有理数,初步感受数形结合的思想方法;
3.能利用数轴比较有理数的大小。
【学习重难点】
数轴的概念及画法。
【学习过程】
一、基础知识回顾
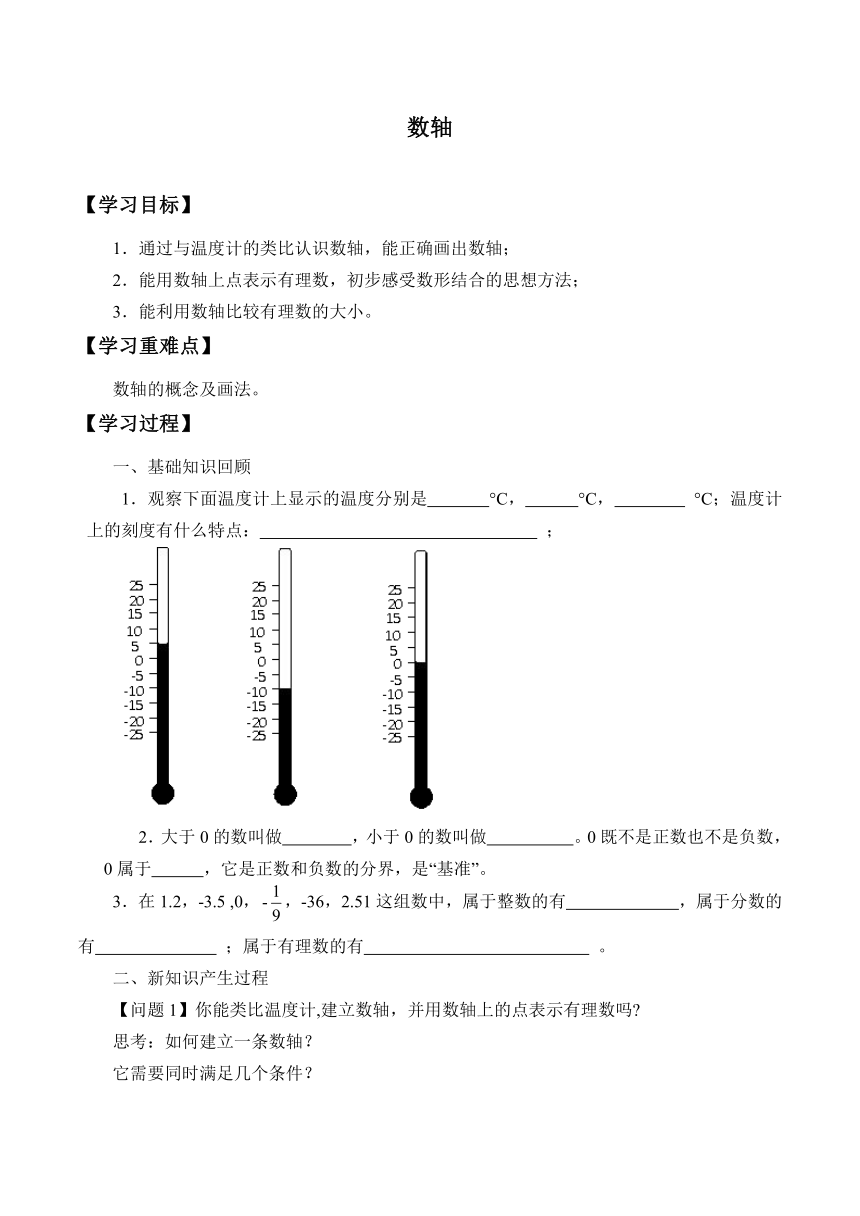
1.观察下面温度计上显示的温度分别是 °C, °C, °C;温度计上的刻度有什么特点: ;
2.大于0的数叫做 ,小于0的数叫做 。0既不是正数也不是负数,0属于 ,它是正数和负数的分界,是“基准”。
3.在1.2,-3.5 ,0,,-36,2.51这组数中,属于整数的有 ,属于分数的有 ;属于有理数的有 。
二、新知识产生过程
【问题1】你能类比温度计,建立数轴,并用数轴上的点表示有理数吗?
思考:如何建立一条数轴?
它需要同时满足几个条件?
1.一般地,画数轴时,先画一条水平直线,在这条直线上取一点作为 ,这点表示为0;规定直线上向右为 ,画上箭头;再选取适当的长度作为 ,这就是数轴要同时满足的三个条件,缺一不可。(注意:单位长度可以由自己选取适当的值,但在0的左右,每个单位长度必须保持均匀一致)
2.请画一条数轴,并标出 +3,-4,0分别在数轴的什么位置? ,-1.5呢?一定要试一试。
解:
由此发现,任何一个有理数都可以用数轴上的一个点来表示。
3.例1:指出数轴上 A, B, C, D各点分别表示什么数?
解:
4.例2:画出数轴,并用数轴上的点表示下列各数:,-3.5,0,5,-4,
解:
归纳思考:从例1可发现,数轴上的某些点可以直观地表示其对应的有理数,这是由“形”到“数”;从例2可发现,一个有理数总可以由数轴上某个点来表示,这是由“数”到“形”; 它们从两个侧面体现出数形结合思想.
【问题2】你能利用数轴上表示有理数的这种数形结合思想,探索如何比较有理数的大小吗?
5.观察右图,可发现:数轴上两个点表示的数,右边点表示的数总比左边的 ;并且向右表示的数越来越 ,向左表示的数越来越 。
归纳得:正数大于0,负数小于0,正数大于负数.
【巩固练习】
1.下列各图表示的数轴是否正确?为什么?
答: ;
答: ;
答: ;
答: ;
2.指出数轴上点A.B.C.D分别表示什么数:A 表示 ,B表示 ,
C表示 ,
D表示 ;
3.比较下列每组数的大小,并说明理由.(利用数轴的数形结合思想)
(1) -2 和 +6; (2) 0和 -1.8; (3) 和 -4;(4)3.8,-4.1和 -3.
解:
4.画出数轴,用数轴上的点表示下列各数: -4, 3.5, -1.5, ,0 , 2.5并用“>”将它们连接起来。
解:
5.写出5个有代表性的有理数,在数轴上将它们表示出来,并比较它们的大小.
解:
6.数轴上与原点的距离是2的点有 个,这些点表示的数是 ;与原点的距离是5的点有 个,这些点表示的数是 。
【学习目标】
1.通过与温度计的类比认识数轴,能正确画出数轴;
2.能用数轴上点表示有理数,初步感受数形结合的思想方法;
3.能利用数轴比较有理数的大小。
【学习重难点】
数轴的概念及画法。
【学习过程】
一、基础知识回顾
1.观察下面温度计上显示的温度分别是 °C, °C, °C;温度计上的刻度有什么特点: ;
2.大于0的数叫做 ,小于0的数叫做 。0既不是正数也不是负数,0属于 ,它是正数和负数的分界,是“基准”。
3.在1.2,-3.5 ,0,,-36,2.51这组数中,属于整数的有 ,属于分数的有 ;属于有理数的有 。
二、新知识产生过程
【问题1】你能类比温度计,建立数轴,并用数轴上的点表示有理数吗?
思考:如何建立一条数轴?
它需要同时满足几个条件?
1.一般地,画数轴时,先画一条水平直线,在这条直线上取一点作为 ,这点表示为0;规定直线上向右为 ,画上箭头;再选取适当的长度作为 ,这就是数轴要同时满足的三个条件,缺一不可。(注意:单位长度可以由自己选取适当的值,但在0的左右,每个单位长度必须保持均匀一致)
2.请画一条数轴,并标出 +3,-4,0分别在数轴的什么位置? ,-1.5呢?一定要试一试。
解:
由此发现,任何一个有理数都可以用数轴上的一个点来表示。
3.例1:指出数轴上 A, B, C, D各点分别表示什么数?
解:
4.例2:画出数轴,并用数轴上的点表示下列各数:,-3.5,0,5,-4,
解:
归纳思考:从例1可发现,数轴上的某些点可以直观地表示其对应的有理数,这是由“形”到“数”;从例2可发现,一个有理数总可以由数轴上某个点来表示,这是由“数”到“形”; 它们从两个侧面体现出数形结合思想.
【问题2】你能利用数轴上表示有理数的这种数形结合思想,探索如何比较有理数的大小吗?
5.观察右图,可发现:数轴上两个点表示的数,右边点表示的数总比左边的 ;并且向右表示的数越来越 ,向左表示的数越来越 。
归纳得:正数大于0,负数小于0,正数大于负数.
【巩固练习】
1.下列各图表示的数轴是否正确?为什么?
答: ;
答: ;
答: ;
答: ;
2.指出数轴上点A.B.C.D分别表示什么数:A 表示 ,B表示 ,
C表示 ,
D表示 ;
3.比较下列每组数的大小,并说明理由.(利用数轴的数形结合思想)
(1) -2 和 +6; (2) 0和 -1.8; (3) 和 -4;(4)3.8,-4.1和 -3.
解:
4.画出数轴,用数轴上的点表示下列各数: -4, 3.5, -1.5, ,0 , 2.5并用“>”将它们连接起来。
解:
5.写出5个有代表性的有理数,在数轴上将它们表示出来,并比较它们的大小.
解:
6.数轴上与原点的距离是2的点有 个,这些点表示的数是 ;与原点的距离是5的点有 个,这些点表示的数是 。
