人教高中数学必修五1.1.1《正弦定理》教案(含教学设计说明)
文档属性
| 名称 | 人教高中数学必修五1.1.1《正弦定理》教案(含教学设计说明) |

|
|
| 格式 | zip | ||
| 文件大小 | 90.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览


文档简介
必修5 1.1 正弦定理和余弦定理
1.1.1 正弦定理
一、教学目标:
1.知识与技能:通过创设问题情境,引导学生发现正弦定理,并推证正弦
定理。会初步运用正弦定理与三角形的内角和定理解斜三角形的两类问题。
2.过程与方法:引导学生从已有的知识出发,共同探究在任意三角形中,边
与其对角正弦的比值之间的关系,培养学生通过观察,猜想,由特殊到一般归纳得出结论的能力和化未知为已知的解决问题的能力。
3.情感、态度与价值观:面向全体学生,创造平等的教学氛围,通过学生
之间、师生之间的交流、合作和评价,调动学生的主动性和积极性,给学生成功的体验,激发学生学习的兴趣。
二、教学重点与难点:
1.重点:正弦定理的探索发现及其初步应用。
2.难点:
①正弦定理的证明;
②了解已知两边和其中一边的对角解三角形时,解的情况不唯一。
三、教学过程:
㈠ 创设情境:
宁静的夜晚,明月高悬,当你仰望夜空,欣赏这美好夜色的时候,会不会想要知道:那遥不可及的月亮离我们究竟有多远呢?1671年两个法国天文学家首次测出了地月之间的距离大约为385400km,你们想知道他们当时是怎样测出这个距离的吗?
学习了本章《解三角形》的内容之后,这个问题就会迎刃而解。
㈡ 新课学习:
⒈提出问题:我们知道,在任意三角形中有大边对大角,小边对小角的边角关系.我们是否能得到这个边、角关系的准确量化的表示呢?
⒉解决问题:
回忆直角三角形中的边角关系:
根据正弦函数的定义有:
,sinC=1。
经过学生思考、交流、讨论得出:
,
问题1:这个结论在任意三角形中还成立吗?
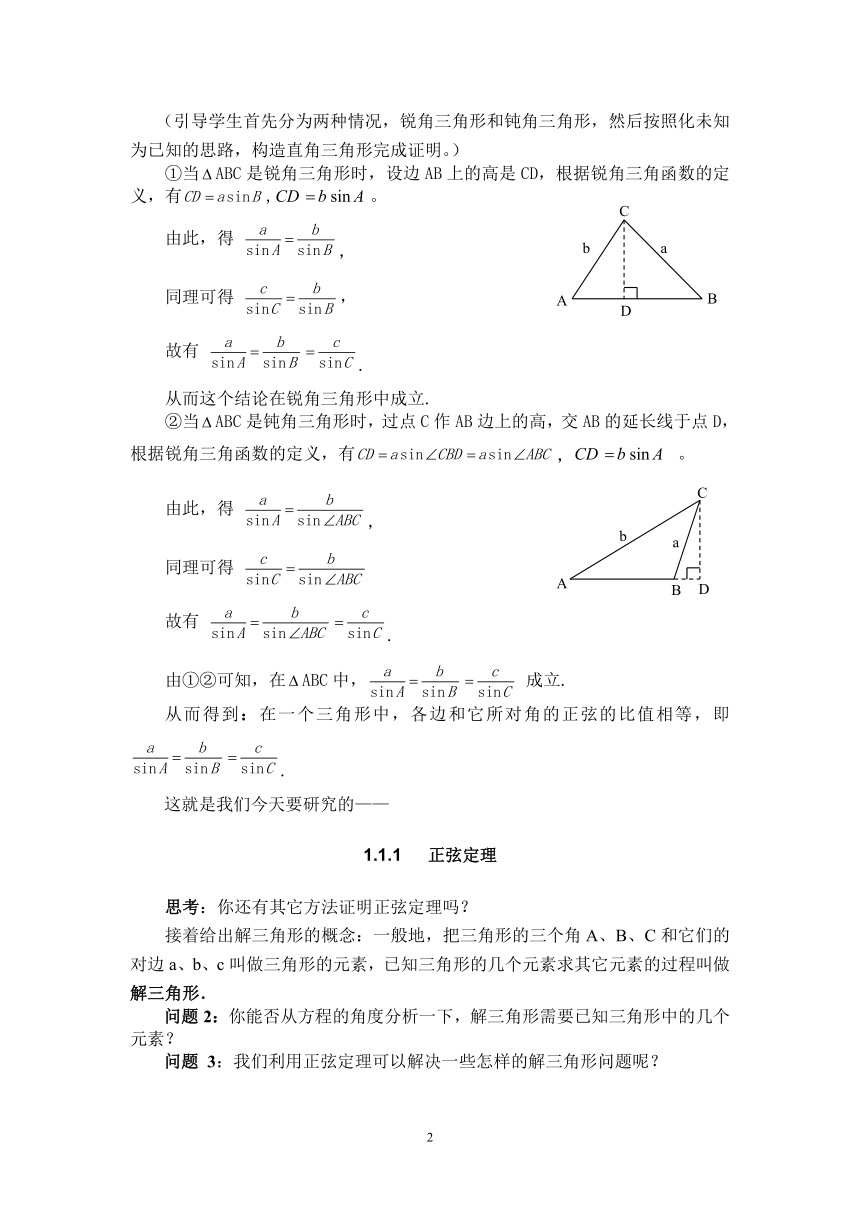
(引导学生首先分为两种情况,锐角三角形和钝角三角形,然后按照化未知为已知的思路,构造直角三角形完成证明。)
①当ABC是锐角三角形时,设边AB上的高是CD,根据锐角三角函数的定义,有,。
由此,得 ,
同理可得 ,
故有 .
从而这个结论在锐角三角形中成立.
②当ABC是钝角三角形时,过点C作AB边上的高,交AB的延长线于点D,根据锐角三角函数的定义,有, 。
由此,得 ,
同理可得
故有 .
由①②可知,在ABC中, 成立.
从而得到:在一个三角形中,各边和它所对角的正弦的比值相等,即.
这就是我们今天要研究的——
1.1.1 正弦定理
思考:你还有其它方法证明正弦定理吗?
接着给出解三角形的概念:一般地,把三角形的三个角A、B、C和它们的对边a、b、c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形.
问题2:你能否从方程的角度分析一下,解三角形需要已知三角形中的几个元素?
问题 3:我们利用正弦定理可以解决一些怎样的解三角形问题呢?
(1)已知三角形的任意两个角与一边,求其他两边和另一角。
(2)已知三角形的两边与其中一边的对角,计算另一边的对角,进而计算出其他的边和角。
3. 应用定理:
例1.
例2.
问题4:你发现运用正弦定理解决的这两类问题的解的情况有什么不同吗?
㈢ 课堂小结:学生发言,互相补充,老师评价.
㈣ 布置作业:
1.思考:已知两边和其中一边的对角,解三角形时,解的情况可能有几种?试
从理论上说明.
2.P10.习题1.1.A组:1.2.
正弦定理教学设计说明
本课的教学内容及其地位和作用
《正弦定理》共2课时,本课是第1课时,学生在初中已经学习了直角三角形中的边角关系和三角形全等的判定,本课是在此基础上继续研究任意三角形中的边角关系,教师带领学生从已有的知识出发,通过探究得到正弦定理,理解定理的内容并能运用正弦定理解三角形的两类问题,结合三角形全等的判定,理解在已知边边角的情况下,三角形解的个数不确定。学生在此之前已经学习了三角函数、平面向量、圆等内容,使得这部分内容的处理有了比较多的工具,教学过程中按照从简原则和最近发展区原则,采用“作高”的方式证明了正弦定理,之后,为了发展学生的思维,学会思考数学问题,又引导学生从向量、作外接圆、三角形面积计算等几个角度找到证明的途径,渗透了事物间普遍联系的辩证唯物主义观点。
本章的中心内容是解三角形,正弦定理是解三角形的重要工具之一,是对三角知识的应用,又是对初中解直角三角形内容的直接延伸,在日常生活和工业生产中也时常有解三角形的问题,在天文、航海测量中也有广泛应用(在下一节中专门研究),充分体现了“数学是有用的”,对培养学生应用数学的意识起到重要作用。
本课的数学本质与教学目标定位
在数学发展史上,受到天文测量、航海测量和地理测量等方面实践活动的推动,解三角形的理论得到不断发展。如:怎样在航行途中测出海上两个岛屿之间的距离?怎样测量底部不可到达的建筑物的高度?怎样测出在海上航行的轮船的航向和航速?……在生产、生活实际中也会遇到例如:怎样确定楼间距,使得一楼的住户也能得到较为充足的阳光?怎样充分利用废旧钢板来节约成本?……这些都是学生非常感兴趣的生活现实,大千世界,数学无处不在,正如荷兰数学家弗赖登塔尔在他所著的《作为教育任务的数学》一书中所讲:“数学起源于现实”,“数学教师的任务之一是帮助学生构造数学现实,并在此基础上发展他们的数学现实。”教学中,通过“如何测出地月之间的距离”来布疑激趣,带领学生进入解三角形内容的学习,通过探究,由特殊到一般得到正弦定理,引导学生多角度思考证明正弦定理,体会数学知识彼此紧密联系的特点,从而感受数学的魅力。
教学过程中,让学生经历提出问题、解决问题、初步应用等过程,使学生成为正弦定理的“发现者”和“创造者”, 《课程标准》将解三角形作为几何度量问题来展开,重在正弦定理在解三角形中的应用,而不必在恒等变换上进行过于繁琐的训练。这就要求在教学中突出几何的作用和数学量化的思想,发挥学生学习的主动性,使学生的学习过程成为在教师引导下的探究、再创造过程。
基于此,本课的教学目标定位在:1. 在创设的问题情境中,引导学生发现正弦定理,推证正弦定理及简单运用正弦定理与三角形内角和定理解斜三角形的两类问题;2. 通过探究在任意三角形中,边与其对角正弦的比值之间的关系,培养学生观察,猜想,由特殊到一般归纳得出结论的能力和化未知为已知解决问题的能力;3.面向全体学生,创造平等的教学氛围,通过学生之间、师生之间的交流、合作和评价,调动学生的主动性和积极性,给学生成功的体验,激发学生学习的兴趣。
教学诊断分析
学生在初中已经学习了锐角三角函数,在必修4中又研究了任意角的三角函数,所以很容易根据直角三角形中的边角关系,得出直角三角形中的正弦定理,从而引出课题:这一结论在任意三角形中还成立吗?证明这个结论是一个难点,特别是钝角三角形中,教师通过引导学生如何化未知为已知,从而找到解决问题的途径。再引导学生思考:什么运算可以把长度和角度联系在一起?从而得到多种解决问题方法。运用定理解三角形不难做到,但是在运用定理的过程中,有一点是学生不容易想到的,也是难以理解的,就是在已知三角形中两边和其中一边的对角时,解的情况不唯一,教师通过引导学生回忆初中所学的三角形全等的判定,“边边角”不能判定三角形全等来理解,本节课只需要让学生知道这一点,详细探究在以后完成。
教法特点和预期效果分析
原苏联数学教育家斯托利亚尔在他所著的《数学教育学》一书中指出:“数学教学是数学活动的教学 ”,“数学活动是思维活动,对数学家而言,这是一个发现活动;对于数学教学来说,我们要教给学生的不是死记现成的材料,而是发现数学真理(自己独立的发现科学上已经发现了的东西),学生发现那些在科学上早已被发现的东西的时候,他是像第一次发现者那样去推理的。”在弗赖登塔尔的论述中也指出:“学生通过自己努力得到的结论和创造是数学教育内容的一部分”。新课标也在倡导积极主动、勇于探索的学习方式。基于这样的理念的指导,结合本课的教学内容,本课采用探究发现式教学法,以“如何测量地月之间的距离”来创设问题情境,以问题驱动课堂,使学生的思维始终活跃于如何解决问题的探究活动中,通过师生之间、生生之间的评价来完善对问题的理解和对定理的应用,创造和谐、愉快、平等的学习氛围,体现学生的主体地位,让学生体验快乐学习,同时培养学生学习数学的兴趣和能力。
本课通过引导学生发现直角三角形中的正弦定理,进而探究在任意三角形中是否还成立?将学生带入探索新知的氛围,学生从已有的知识经验出发,探索得出新结论,体验了成功的乐趣,对如何运用定理解决问题也是跃跃欲试,例题教学中,展示学生答案之后,给全体学生一个畅所欲言的机会,互相评价,最终得到完善的答案,在集体交流中感受合作的巨大力量。这样做,对于不善于表达自己的学生可能会失去和大家交流的机会,但通过老师和学生的鼓励,也可以克服。这也体现了一个人成长、发展所必须经历的过程,对于培养意志品质起到了重要作用。
C
B
A
c
b
a
a
b
D
A
B
C
A
B
C
D
b
a
PAGE
7
1.1.1 正弦定理
一、教学目标:
1.知识与技能:通过创设问题情境,引导学生发现正弦定理,并推证正弦
定理。会初步运用正弦定理与三角形的内角和定理解斜三角形的两类问题。
2.过程与方法:引导学生从已有的知识出发,共同探究在任意三角形中,边
与其对角正弦的比值之间的关系,培养学生通过观察,猜想,由特殊到一般归纳得出结论的能力和化未知为已知的解决问题的能力。
3.情感、态度与价值观:面向全体学生,创造平等的教学氛围,通过学生
之间、师生之间的交流、合作和评价,调动学生的主动性和积极性,给学生成功的体验,激发学生学习的兴趣。
二、教学重点与难点:
1.重点:正弦定理的探索发现及其初步应用。
2.难点:
①正弦定理的证明;
②了解已知两边和其中一边的对角解三角形时,解的情况不唯一。
三、教学过程:
㈠ 创设情境:
宁静的夜晚,明月高悬,当你仰望夜空,欣赏这美好夜色的时候,会不会想要知道:那遥不可及的月亮离我们究竟有多远呢?1671年两个法国天文学家首次测出了地月之间的距离大约为385400km,你们想知道他们当时是怎样测出这个距离的吗?
学习了本章《解三角形》的内容之后,这个问题就会迎刃而解。
㈡ 新课学习:
⒈提出问题:我们知道,在任意三角形中有大边对大角,小边对小角的边角关系.我们是否能得到这个边、角关系的准确量化的表示呢?
⒉解决问题:
回忆直角三角形中的边角关系:
根据正弦函数的定义有:
,sinC=1。
经过学生思考、交流、讨论得出:
,
问题1:这个结论在任意三角形中还成立吗?
(引导学生首先分为两种情况,锐角三角形和钝角三角形,然后按照化未知为已知的思路,构造直角三角形完成证明。)
①当ABC是锐角三角形时,设边AB上的高是CD,根据锐角三角函数的定义,有,。
由此,得 ,
同理可得 ,
故有 .
从而这个结论在锐角三角形中成立.
②当ABC是钝角三角形时,过点C作AB边上的高,交AB的延长线于点D,根据锐角三角函数的定义,有, 。
由此,得 ,
同理可得
故有 .
由①②可知,在ABC中, 成立.
从而得到:在一个三角形中,各边和它所对角的正弦的比值相等,即.
这就是我们今天要研究的——
1.1.1 正弦定理
思考:你还有其它方法证明正弦定理吗?
接着给出解三角形的概念:一般地,把三角形的三个角A、B、C和它们的对边a、b、c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形.
问题2:你能否从方程的角度分析一下,解三角形需要已知三角形中的几个元素?
问题 3:我们利用正弦定理可以解决一些怎样的解三角形问题呢?
(1)已知三角形的任意两个角与一边,求其他两边和另一角。
(2)已知三角形的两边与其中一边的对角,计算另一边的对角,进而计算出其他的边和角。
3. 应用定理:
例1.
例2.
问题4:你发现运用正弦定理解决的这两类问题的解的情况有什么不同吗?
㈢ 课堂小结:学生发言,互相补充,老师评价.
㈣ 布置作业:
1.思考:已知两边和其中一边的对角,解三角形时,解的情况可能有几种?试
从理论上说明.
2.P10.习题1.1.A组:1.2.
正弦定理教学设计说明
本课的教学内容及其地位和作用
《正弦定理》共2课时,本课是第1课时,学生在初中已经学习了直角三角形中的边角关系和三角形全等的判定,本课是在此基础上继续研究任意三角形中的边角关系,教师带领学生从已有的知识出发,通过探究得到正弦定理,理解定理的内容并能运用正弦定理解三角形的两类问题,结合三角形全等的判定,理解在已知边边角的情况下,三角形解的个数不确定。学生在此之前已经学习了三角函数、平面向量、圆等内容,使得这部分内容的处理有了比较多的工具,教学过程中按照从简原则和最近发展区原则,采用“作高”的方式证明了正弦定理,之后,为了发展学生的思维,学会思考数学问题,又引导学生从向量、作外接圆、三角形面积计算等几个角度找到证明的途径,渗透了事物间普遍联系的辩证唯物主义观点。
本章的中心内容是解三角形,正弦定理是解三角形的重要工具之一,是对三角知识的应用,又是对初中解直角三角形内容的直接延伸,在日常生活和工业生产中也时常有解三角形的问题,在天文、航海测量中也有广泛应用(在下一节中专门研究),充分体现了“数学是有用的”,对培养学生应用数学的意识起到重要作用。
本课的数学本质与教学目标定位
在数学发展史上,受到天文测量、航海测量和地理测量等方面实践活动的推动,解三角形的理论得到不断发展。如:怎样在航行途中测出海上两个岛屿之间的距离?怎样测量底部不可到达的建筑物的高度?怎样测出在海上航行的轮船的航向和航速?……在生产、生活实际中也会遇到例如:怎样确定楼间距,使得一楼的住户也能得到较为充足的阳光?怎样充分利用废旧钢板来节约成本?……这些都是学生非常感兴趣的生活现实,大千世界,数学无处不在,正如荷兰数学家弗赖登塔尔在他所著的《作为教育任务的数学》一书中所讲:“数学起源于现实”,“数学教师的任务之一是帮助学生构造数学现实,并在此基础上发展他们的数学现实。”教学中,通过“如何测出地月之间的距离”来布疑激趣,带领学生进入解三角形内容的学习,通过探究,由特殊到一般得到正弦定理,引导学生多角度思考证明正弦定理,体会数学知识彼此紧密联系的特点,从而感受数学的魅力。
教学过程中,让学生经历提出问题、解决问题、初步应用等过程,使学生成为正弦定理的“发现者”和“创造者”, 《课程标准》将解三角形作为几何度量问题来展开,重在正弦定理在解三角形中的应用,而不必在恒等变换上进行过于繁琐的训练。这就要求在教学中突出几何的作用和数学量化的思想,发挥学生学习的主动性,使学生的学习过程成为在教师引导下的探究、再创造过程。
基于此,本课的教学目标定位在:1. 在创设的问题情境中,引导学生发现正弦定理,推证正弦定理及简单运用正弦定理与三角形内角和定理解斜三角形的两类问题;2. 通过探究在任意三角形中,边与其对角正弦的比值之间的关系,培养学生观察,猜想,由特殊到一般归纳得出结论的能力和化未知为已知解决问题的能力;3.面向全体学生,创造平等的教学氛围,通过学生之间、师生之间的交流、合作和评价,调动学生的主动性和积极性,给学生成功的体验,激发学生学习的兴趣。
教学诊断分析
学生在初中已经学习了锐角三角函数,在必修4中又研究了任意角的三角函数,所以很容易根据直角三角形中的边角关系,得出直角三角形中的正弦定理,从而引出课题:这一结论在任意三角形中还成立吗?证明这个结论是一个难点,特别是钝角三角形中,教师通过引导学生如何化未知为已知,从而找到解决问题的途径。再引导学生思考:什么运算可以把长度和角度联系在一起?从而得到多种解决问题方法。运用定理解三角形不难做到,但是在运用定理的过程中,有一点是学生不容易想到的,也是难以理解的,就是在已知三角形中两边和其中一边的对角时,解的情况不唯一,教师通过引导学生回忆初中所学的三角形全等的判定,“边边角”不能判定三角形全等来理解,本节课只需要让学生知道这一点,详细探究在以后完成。
教法特点和预期效果分析
原苏联数学教育家斯托利亚尔在他所著的《数学教育学》一书中指出:“数学教学是数学活动的教学 ”,“数学活动是思维活动,对数学家而言,这是一个发现活动;对于数学教学来说,我们要教给学生的不是死记现成的材料,而是发现数学真理(自己独立的发现科学上已经发现了的东西),学生发现那些在科学上早已被发现的东西的时候,他是像第一次发现者那样去推理的。”在弗赖登塔尔的论述中也指出:“学生通过自己努力得到的结论和创造是数学教育内容的一部分”。新课标也在倡导积极主动、勇于探索的学习方式。基于这样的理念的指导,结合本课的教学内容,本课采用探究发现式教学法,以“如何测量地月之间的距离”来创设问题情境,以问题驱动课堂,使学生的思维始终活跃于如何解决问题的探究活动中,通过师生之间、生生之间的评价来完善对问题的理解和对定理的应用,创造和谐、愉快、平等的学习氛围,体现学生的主体地位,让学生体验快乐学习,同时培养学生学习数学的兴趣和能力。
本课通过引导学生发现直角三角形中的正弦定理,进而探究在任意三角形中是否还成立?将学生带入探索新知的氛围,学生从已有的知识经验出发,探索得出新结论,体验了成功的乐趣,对如何运用定理解决问题也是跃跃欲试,例题教学中,展示学生答案之后,给全体学生一个畅所欲言的机会,互相评价,最终得到完善的答案,在集体交流中感受合作的巨大力量。这样做,对于不善于表达自己的学生可能会失去和大家交流的机会,但通过老师和学生的鼓励,也可以克服。这也体现了一个人成长、发展所必须经历的过程,对于培养意志品质起到了重要作用。
C
B
A
c
b
a
a
b
D
A
B
C
A
B
C
D
b
a
PAGE
7
