2019-2020学年北师大版数学选修2-2第一章推理与证明 课件:43张PPT
文档属性
| 名称 | 2019-2020学年北师大版数学选修2-2第一章推理与证明 课件:43张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 16:08:40 | ||
图片预览











文档简介
课件43张PPT。第一章推理与证明同学们,你知道人造地球卫星在太空中是怎样运行与工作的吗?你知道人们怎样认识浩瀚无际的宇宙的吗?你看过《福尔摩斯探案集》吗?你了解哥德巴赫猜想吗?你知道考古学家怎样推断遗址的年代,医生怎样诊断病人的疾病,警察怎样破案,气象专家怎样预测天气,数学家怎样论证命题的真伪吗?这一切都离不开推理.而证明的过程更离不开推理.
本章我们将学习两种基本推理——合情推理与演绎推理.学习数学证明的基本方法——分析法、综合法、反证法等.要通过本章的学习养成言之有据,证明过程语言条理、逻辑规范的好习惯. §1 归纳与类比自主预习学案 《内经·针刺篇》记载了这样一个故事:有一个患
头痛的樵夫上山砍柴,一次不慎碰破脚趾,出了一
点血,但头不疼了.当时他没有注意.后来头疼复
发,又偶然碰破同一脚趾,头疼又好了.这次引起
了他的注意,以后每次头疼时,他就有意刺破该处,
都有效应(这个樵夫碰的地方,即现在所称的“大敦穴”).现在我们要问,为什么这个樵夫以后头疼时就想到要刺破原脚趾处呢?这里面有怎样的数学知识呢?1.推理的概念
根据一个或几个已知的事实(或假设)得出一个判断,这种思维方式叫推理.推理一般由两部分组成:_____和_____.
2.合理推理
(1)当前提为真时,结论__________的推理,叫做合情推理.前提 结论 可能为真 合情推理是指“合乎情理”的推理.数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论;证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向,其推理过程为:
(2)两种合情推理:_________和_________.
3.归纳推理的定义
根据一类事物中部分事物具有某种属性,推断_________________________ _________,这种推理方式称为归纳推理(简称归纳).
归纳推理是由部分到整体,由_____到_____的推理.
利用归纳推理得出的结论不一定是正确的.一般地,如果归纳的个别情况越多,越具有代表性,那么推广的一般性结论也就越可靠.归纳推理 类比推理 该类事物中每一个事物都有 个别 一般 这种属性 4.类比推理的定义
由于两类不同对象具有某些类似的特征,在此基础上,根据一类对象的其他特征,推断另一类对象也_____________________,这种推理方式称为类比推理(简称类比).
类比推理是由_______到_______的推理,是两类事物特征之间的推理.
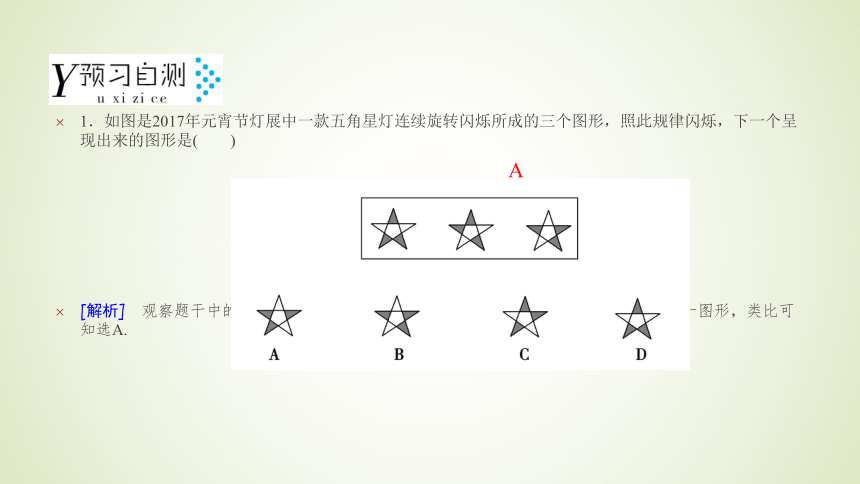
利用类比推理得出的结论不一定是正确的.一般地,如果类比的两类对象的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的结论就越可靠.具有类似的其他特征 特殊 特殊 1.如图是2017年元宵节灯展中一款五角星灯连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是( )
[解析] 观察题干中的三个图形,前一个图形以中心为原点沿顺时针旋转144°得到后一图形,类比可知选A.A 2.下面类比推理中恰当的是( )
A.“若a·3=b·3,则a=b”类比推出“若a·0=b·0,则a=b”
B.“(a+b)c=ac+bc”类比推出“(a·b)c=ac·bc”
D.“(ab)n=anbn”类比推出“(a+b)n=an+bn”
[解析] 结合实数的运算律知C是正确的.C 3.等差数列{an}中,an>0,公差d>0,则有a4·a6>a3·a7,类比上述性质,在等比数列{bn}中,若bn>0,q>1,写出b5,b7,b4,b8的一个不等关系________________.
[解析] 将乘积与和对应,再注意下标的对应,有b4+b8>b5+b7.b4+b8>b5+b7 互动探究学案 (1)观察分析下表中的数据:
猜想一般凸多面体中,F,V,E所满足的等式是________________.命题方向1 ?归纳推理典例 1 V+F-E=2 (2)(2019·聊城高二检测)由下列各式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
请你归纳出一般结论.
[思路分析] (1)通过观察几组数字之间的关系列式;
(2)通过观察等式左右各自特点找通项.[解析] (1)因为5+6-9=2,
6+6-10=2,
6+8-12=2,
∴V+F-E=2.『规律总结』 (1)由已知数式进行归纳推理的步骤
①分析所给几个等式(或不等式)中项数和次数等方面的变化规律或结构形式的特征.
②提炼出等式(或不等式)的综合特点.
③运用归纳推理得出一般结论.(2)归纳推理在图形中的应用策略
〔跟踪练习1〕
下图是用同样规格的灰、白两色正方形瓷砖铺设的若干图案,则按此规律,第n个图案中需用灰色瓷砖________块(用含n的代数式表示).
[解析] 第(1),(2),(3),…个图案灰色瓷砖数依次为15-3=12,24-8=16,35-15=20,……
由此可猜测第n个图案灰色瓷砖数为(n+2)(n+4)-n(n+2)=4(n+2)=4n+8.4n+8 命题方向2 ?类比推理典例 2 [思路分析] 考虑到用“面积法”证明结论时把O点与三角形的三个顶点连接,把三角形分成三个三角形,利用面积相等来证明相应的结论.在证明四面体中类似结论时,可考虑利用体积相等的方法证明相应的结论.『规律总结』 1.类比推理的思维过程大致为:
2.类比推理的一般步骤:
(1)通过观察、分析,找出两类事物之间的相似性或一致性.
(2)通过类比、联想,用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).
(3)通过推理论证,证明结论或推翻结论.
一般情况下,如果类比的两类事物的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的结论就越可靠.类比推理的结论既可能真,也可能假,它是一种由特殊到特殊的认识过程,具有十分重要的实用价值.〔跟踪练习2〕[解析] 如图所示,设A在底面的射影为O,连接BO并延长交CD于E.连接AE,由AB⊥AC,AB⊥AD得AB⊥平面ACD.归纳推理具有从特殊到一般,从具体到抽象的认知功能,在求数列的通项公式或前n项和的问题中,经常用归纳推理得出关于前有限项的结论,此时要注意把它们的表达式的结构形式进行统一,以便于寻找规律,归纳猜想得出结论.
其具体步骤是:
(1)通过条件求得数列中的前几项;
(2)观察数列的前几项寻求项的规律,猜测数列的通项公式.归纳推理在数列中的应用 已知数列{an}满足a1=1,an+1=2an+1(n=1,2,3,…)
(1)求a2,a3,a4,a5;
(2)归纳猜想通项an的表达式.典例 3 [解析] (1)已知a1=1,an+1=2an+1,则a2=2×1+1=3,a3=2×3+1=7,a4=2×7+1=15,a5=2×15+1=31.
(2)由a1=1=21-1,
a2=3=22-1,
a3=7=23-1,
a4=15=24-1,
a5=31=25-1,
可归纳猜想出an=2n-1(n∈N*).『规律总结』 (1)根据给出的几个具体等式归纳其一般结论时,要注意从等式的项数、次数、分式的分子与分母各自的特点及变化规律入手进行归纳,要注意等式中项数、次数等与等式序号n的关系,发现其规律,然后用含有字母的等式表示一般性结论.
(2)解决数列中的归纳推理问题时,通常是将所给等式中的n取具体值1,2,3,4,…,然后求得a1,a2,a3,a4,…的值或S1,S2,S3,S4,…的值,根据这些结果进行归纳得到结果. 在下列类比推理中,正确的有__________.
①把a(b+c)与loga(x+y)类比,则有loga(x+y)=logax+logay.
②把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny.
③把实数a,b满足:“若ab=0,b≠0,则a=0”.类比平面向量的数量积,“若a·b=0,b≠0,则a=0”.典例 4 [错解] ②③
[辨析] 没有抓住类比推理的实质.
[正解] ④ ①②中,loga(x+y)与sin(x+y)都是一个整体,而a(b+c)中a与b+c是两个各自独立的部分,它们之间没有可类比性;③中由a,b两数的积,类比到a,b两向量的数量积,类比形式正确,但类比结论错误;④中,将平面上直线将三角形分成两部分的面积比、类比到空间中平面将三棱锥分成两部分的体积比,将角的两边,类比到二面角的两个面,类比形式正确,易证类比结论也是正确的.
[点评] 进行类比推理时,要从其形式、结构、维数等类似特征入手,要抓住本质属性中相似或相同之处作类比.玉 〔跟踪练习4〕
在Rt△ABC中,C为直角,A,B,C所对的边的长分别为a,b,c,则c2=a2+b2,类比在三棱锥中有何结论.[解析] 观察可发现规律:①每行、每列中,方、圆、三角三种形状均各出现一次,②每行、每列有两阴影一空白,即得结果.A 2.鲁班发明锯子的思维过程为:带齿的草叶能割破行人的腿,“锯子”能“锯”开木材,它们在功能上是类似的.因此,它们在形状上也应该类似,“锯子”应该是齿形的.该过程体现了( )
A.归纳推理 B.类比推理
C.没有推理 D.以上说法都不对
[解析] 推理是根据一个或几个已知的判断来确定一个新的判断的思维过程,上述过程是推理,由性质类比可知是类比推理.B 3.平面内的小圆形按照下图中的规律排列,每个图中的圆的个数构成一个数列{an},则下列结论正确的是( )
①a5=15;
②数列{an}是一个等差数列;
③数列{an}是一个等比数列;
④数列{an}的递推关系是an=an-1+n(n∈N*).
A.①②④ B.①③④
C.①② D.①④D [解析] 由于a1=1,a2=3,a3=6,a4=10,所以有a2-a1=2,a3-a2=3,a4-a3=4.因此必有a5-a4=5,即a5=15,故①正确.同时④正确,而{an}显然不是等差数列也不是等比数列,故②③错误,故选D.4.观察下列等式:
12=1,
12-22=-3,
12-22+32=6,
12-22+32-42=-10,
……
由以上等式推测到一个一般的结论:对于n∈N*,12-22+32-42+…+(-1)n+1n2=_____________.
本章我们将学习两种基本推理——合情推理与演绎推理.学习数学证明的基本方法——分析法、综合法、反证法等.要通过本章的学习养成言之有据,证明过程语言条理、逻辑规范的好习惯. §1 归纳与类比自主预习学案 《内经·针刺篇》记载了这样一个故事:有一个患
头痛的樵夫上山砍柴,一次不慎碰破脚趾,出了一
点血,但头不疼了.当时他没有注意.后来头疼复
发,又偶然碰破同一脚趾,头疼又好了.这次引起
了他的注意,以后每次头疼时,他就有意刺破该处,
都有效应(这个樵夫碰的地方,即现在所称的“大敦穴”).现在我们要问,为什么这个樵夫以后头疼时就想到要刺破原脚趾处呢?这里面有怎样的数学知识呢?1.推理的概念
根据一个或几个已知的事实(或假设)得出一个判断,这种思维方式叫推理.推理一般由两部分组成:_____和_____.
2.合理推理
(1)当前提为真时,结论__________的推理,叫做合情推理.前提 结论 可能为真 合情推理是指“合乎情理”的推理.数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论;证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向,其推理过程为:
(2)两种合情推理:_________和_________.
3.归纳推理的定义
根据一类事物中部分事物具有某种属性,推断_________________________ _________,这种推理方式称为归纳推理(简称归纳).
归纳推理是由部分到整体,由_____到_____的推理.
利用归纳推理得出的结论不一定是正确的.一般地,如果归纳的个别情况越多,越具有代表性,那么推广的一般性结论也就越可靠.归纳推理 类比推理 该类事物中每一个事物都有 个别 一般 这种属性 4.类比推理的定义
由于两类不同对象具有某些类似的特征,在此基础上,根据一类对象的其他特征,推断另一类对象也_____________________,这种推理方式称为类比推理(简称类比).
类比推理是由_______到_______的推理,是两类事物特征之间的推理.
利用类比推理得出的结论不一定是正确的.一般地,如果类比的两类对象的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的结论就越可靠.具有类似的其他特征 特殊 特殊 1.如图是2017年元宵节灯展中一款五角星灯连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是( )
[解析] 观察题干中的三个图形,前一个图形以中心为原点沿顺时针旋转144°得到后一图形,类比可知选A.A 2.下面类比推理中恰当的是( )
A.“若a·3=b·3,则a=b”类比推出“若a·0=b·0,则a=b”
B.“(a+b)c=ac+bc”类比推出“(a·b)c=ac·bc”
D.“(ab)n=anbn”类比推出“(a+b)n=an+bn”
[解析] 结合实数的运算律知C是正确的.C 3.等差数列{an}中,an>0,公差d>0,则有a4·a6>a3·a7,类比上述性质,在等比数列{bn}中,若bn>0,q>1,写出b5,b7,b4,b8的一个不等关系________________.
[解析] 将乘积与和对应,再注意下标的对应,有b4+b8>b5+b7.b4+b8>b5+b7 互动探究学案 (1)观察分析下表中的数据:
猜想一般凸多面体中,F,V,E所满足的等式是________________.命题方向1 ?归纳推理典例 1 V+F-E=2 (2)(2019·聊城高二检测)由下列各式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
请你归纳出一般结论.
[思路分析] (1)通过观察几组数字之间的关系列式;
(2)通过观察等式左右各自特点找通项.[解析] (1)因为5+6-9=2,
6+6-10=2,
6+8-12=2,
∴V+F-E=2.『规律总结』 (1)由已知数式进行归纳推理的步骤
①分析所给几个等式(或不等式)中项数和次数等方面的变化规律或结构形式的特征.
②提炼出等式(或不等式)的综合特点.
③运用归纳推理得出一般结论.(2)归纳推理在图形中的应用策略
〔跟踪练习1〕
下图是用同样规格的灰、白两色正方形瓷砖铺设的若干图案,则按此规律,第n个图案中需用灰色瓷砖________块(用含n的代数式表示).
[解析] 第(1),(2),(3),…个图案灰色瓷砖数依次为15-3=12,24-8=16,35-15=20,……
由此可猜测第n个图案灰色瓷砖数为(n+2)(n+4)-n(n+2)=4(n+2)=4n+8.4n+8 命题方向2 ?类比推理典例 2 [思路分析] 考虑到用“面积法”证明结论时把O点与三角形的三个顶点连接,把三角形分成三个三角形,利用面积相等来证明相应的结论.在证明四面体中类似结论时,可考虑利用体积相等的方法证明相应的结论.『规律总结』 1.类比推理的思维过程大致为:
2.类比推理的一般步骤:
(1)通过观察、分析,找出两类事物之间的相似性或一致性.
(2)通过类比、联想,用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).
(3)通过推理论证,证明结论或推翻结论.
一般情况下,如果类比的两类事物的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的结论就越可靠.类比推理的结论既可能真,也可能假,它是一种由特殊到特殊的认识过程,具有十分重要的实用价值.〔跟踪练习2〕[解析] 如图所示,设A在底面的射影为O,连接BO并延长交CD于E.连接AE,由AB⊥AC,AB⊥AD得AB⊥平面ACD.归纳推理具有从特殊到一般,从具体到抽象的认知功能,在求数列的通项公式或前n项和的问题中,经常用归纳推理得出关于前有限项的结论,此时要注意把它们的表达式的结构形式进行统一,以便于寻找规律,归纳猜想得出结论.
其具体步骤是:
(1)通过条件求得数列中的前几项;
(2)观察数列的前几项寻求项的规律,猜测数列的通项公式.归纳推理在数列中的应用 已知数列{an}满足a1=1,an+1=2an+1(n=1,2,3,…)
(1)求a2,a3,a4,a5;
(2)归纳猜想通项an的表达式.典例 3 [解析] (1)已知a1=1,an+1=2an+1,则a2=2×1+1=3,a3=2×3+1=7,a4=2×7+1=15,a5=2×15+1=31.
(2)由a1=1=21-1,
a2=3=22-1,
a3=7=23-1,
a4=15=24-1,
a5=31=25-1,
可归纳猜想出an=2n-1(n∈N*).『规律总结』 (1)根据给出的几个具体等式归纳其一般结论时,要注意从等式的项数、次数、分式的分子与分母各自的特点及变化规律入手进行归纳,要注意等式中项数、次数等与等式序号n的关系,发现其规律,然后用含有字母的等式表示一般性结论.
(2)解决数列中的归纳推理问题时,通常是将所给等式中的n取具体值1,2,3,4,…,然后求得a1,a2,a3,a4,…的值或S1,S2,S3,S4,…的值,根据这些结果进行归纳得到结果. 在下列类比推理中,正确的有__________.
①把a(b+c)与loga(x+y)类比,则有loga(x+y)=logax+logay.
②把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny.
③把实数a,b满足:“若ab=0,b≠0,则a=0”.类比平面向量的数量积,“若a·b=0,b≠0,则a=0”.典例 4 [错解] ②③
[辨析] 没有抓住类比推理的实质.
[正解] ④ ①②中,loga(x+y)与sin(x+y)都是一个整体,而a(b+c)中a与b+c是两个各自独立的部分,它们之间没有可类比性;③中由a,b两数的积,类比到a,b两向量的数量积,类比形式正确,但类比结论错误;④中,将平面上直线将三角形分成两部分的面积比、类比到空间中平面将三棱锥分成两部分的体积比,将角的两边,类比到二面角的两个面,类比形式正确,易证类比结论也是正确的.
[点评] 进行类比推理时,要从其形式、结构、维数等类似特征入手,要抓住本质属性中相似或相同之处作类比.玉 〔跟踪练习4〕
在Rt△ABC中,C为直角,A,B,C所对的边的长分别为a,b,c,则c2=a2+b2,类比在三棱锥中有何结论.[解析] 观察可发现规律:①每行、每列中,方、圆、三角三种形状均各出现一次,②每行、每列有两阴影一空白,即得结果.A 2.鲁班发明锯子的思维过程为:带齿的草叶能割破行人的腿,“锯子”能“锯”开木材,它们在功能上是类似的.因此,它们在形状上也应该类似,“锯子”应该是齿形的.该过程体现了( )
A.归纳推理 B.类比推理
C.没有推理 D.以上说法都不对
[解析] 推理是根据一个或几个已知的判断来确定一个新的判断的思维过程,上述过程是推理,由性质类比可知是类比推理.B 3.平面内的小圆形按照下图中的规律排列,每个图中的圆的个数构成一个数列{an},则下列结论正确的是( )
①a5=15;
②数列{an}是一个等差数列;
③数列{an}是一个等比数列;
④数列{an}的递推关系是an=an-1+n(n∈N*).
A.①②④ B.①③④
C.①② D.①④D [解析] 由于a1=1,a2=3,a3=6,a4=10,所以有a2-a1=2,a3-a2=3,a4-a3=4.因此必有a5-a4=5,即a5=15,故①正确.同时④正确,而{an}显然不是等差数列也不是等比数列,故②③错误,故选D.4.观察下列等式:
12=1,
12-22=-3,
12-22+32=6,
12-22+32-42=-10,
……
由以上等式推测到一个一般的结论:对于n∈N*,12-22+32-42+…+(-1)n+1n2=_____________.
同课章节目录
