2019-2020学年北师大版数学选修2-2第一章推理与证明本章总结课件:40张PPT
文档属性
| 名称 | 2019-2020学年北师大版数学选修2-2第一章推理与证明本章总结课件:40张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 606.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 16:00:56 | ||
图片预览










文档简介
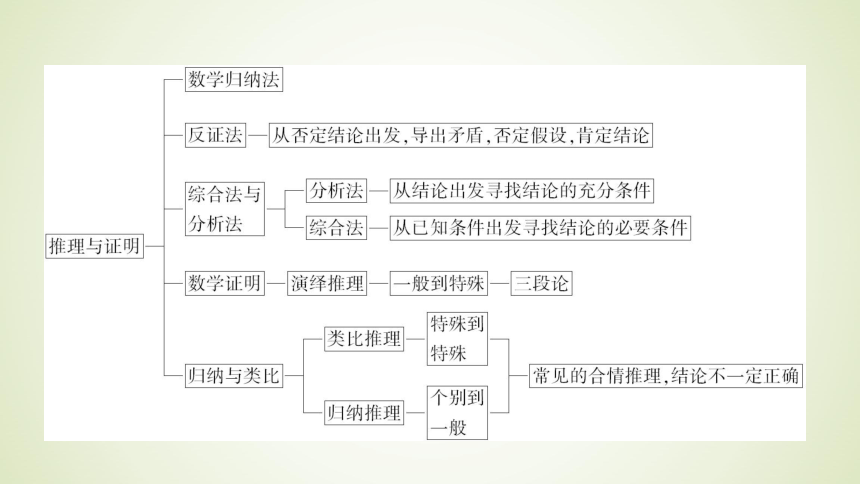
课件40张PPT。第一章推理与证明本章总结1.合情推理分为归纳推理和类比推理,是基本的分析和解决问题的方法.合情推理是合乎情理的推理,通过归纳、猜测发现结论,为解决问题提供了思路和方向.归纳推理和类比推理的特点与区别:类比推理和归纳推理的结论都是有待于证明的.归纳推理是由特殊到一般的推理,类比推理是由特殊到特殊的推理.
2.演绎推理
演绎推理是数学证明中的基本推理形式,“三段论”是演绎推理的一般模式.专题一 ?归纳与类比3.近几年高考对推理的考查:
(1)以选择题、填空题的形式考查合情推理;
(2)以选择题或解答题的形式考查演绎推理;
(3)题目难度不大,多以中低档题为主. 将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … … …
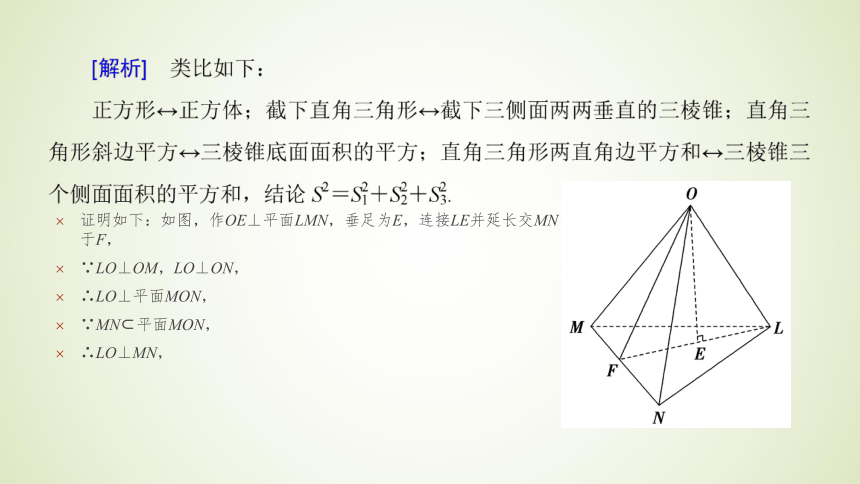
根据以上排列规律,数阵中第n(n≥3)行的从左至右的第3个数为_________.典例 1 在平面上,我们用一直线去截正方形的一个角,那么截下的一个直角三角形,按如图所标边长,由勾股定理有c2=a2+b2.设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1、S2、S3表示三个侧面面积,S表示截面面积,那么类比得到的结论是______________.典例 2 证明如下:如图,作OE⊥平面LMN,垂足为E,连接LE并延长交MN于F,
∵LO⊥OM,LO⊥ON,
∴LO⊥平面MON,
∵MN?平面MON,
∴LO⊥MN,『规律方法』 类比推理应从具体问题出发,通过观察、分析、类比、归纳而得出结论.通常情况下,平面图形的边长、面积往往类比空间几何体的面积、体积.综合与分析法是证明命题的两种最基本、最常用的直接证明方法.综合法常用于由已知推论较易找到思路时;分析法常用于条件复杂、思考方向不明确且用综合法较难证明时.单纯应用分析法证明并不多见,常常是用分析法寻找思路,用综合法表述过程.因此在实际应用中,经常要把综合法与分析法结合起来使用.本考点在高考中每年都要涉及,主要以考查直接证明中的综合法为主.专题二 ?直接证明 (2019·清水县期中)设a>0,b>0,2c>a+b,求证:
(1)c2>ab;
[思路分析] (1)根据基本不等式的证明即可证明c2>ab;
(2)利用分析法进行证明.典例 3 反证法是间接证明的一种基本方法,它不去直接证明结论,而是先否定结论,在否定结论的基础上,运用正确的推理,导出矛盾,从而肯定结论的真实性.在证明一些否定性命题、唯一性命题或含有“至多”“至少”等字样的命题时,正面证明往往较难,此时可考虑反证法,即“正难则反”.
设{an}是公比为q的等比数列.
(1)推导{an}的前n项和公式.
(2)设q≠1,证明:数列{an+1}不是等比数列.专题三 ?用反证法证明典例 4 [解析] (1)分两种情况讨论.
①当q=1时,数列{an}是首项为a1的常数数列,所以Sn=a1+a1+…+a1=na1.
②当q≠1时,Sn=a1+a2+…+an-1+an?qSn=qa1+qa2+…+qan-1+qan.
上面两式错位相减:
(1-q)Sn=a1+(a2-qa1)+(a3-qa2)+…+(an-qan-1)-qan=a1-qan(2)使用反证法.
设{an}是公比q≠1的等比数列,假设数列{an+1}是等比数列,则
(a2+1)2=(a1+1)(a3+1)即(a1q+1)2
=(a1+1)(a1q2+1),
整理得a1(q-1)2=0得a1=0或q=1均与题设矛盾,故数列{an+1}不是等比数列.『规律方法』 用反证法证明问题时要注意以下三点
(1)必须否定结论,即肯定结论的反面,当结论的反面呈现多样性时,必须罗列出各种可能结论,缺少任何一种可能,都不是反证法.
(2)反证法必须从否定结论进行推证,即应把结论的反面作为条件,且必须根据这一条件进行推证,否则,仅否定结论,不从结论的反面出发进行推理,就不是反证法.
(3)推导出的矛盾可能多种多样,有的与已知矛盾,有的与假设矛盾,有的与事实矛盾等,但是推导出的矛盾必须是明显的.数学归纳法是一种证明方法,可以证明与正整数有关的命题,如恒等式、不等式、几何问题以及整除问题等.高考数学归纳法的考查,一般以数列为背景,涉及等式、不等式等问题,归纳—猜想—证明是解决此问题的通法.
在数列{an}与{bn}中,a1=1,b1=4,数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0,2an+1为bn与bn+1的等比中项,n∈N*.
(1)求a2,b2的值;
(2)求数列{an}与{bn}的通项公式.专题四 ?用数学归纳法解题典例 5 『规律总结』 数学归纳法的主要思想:数学归纳法中两个步骤体现了递推思想,第一步是递推基础,也叫归纳奠基;第二步是递推的依据,也叫归纳递推.在这一步中归纳假设必须用上,否则就不是数学归纳法.转化与化归的思想方法是数学最基本的思想方法,数学中一切问题的解决都离不开转化与化归.转化与化归是数学思想方法的灵魂.在本章中,合情推理与演绎推理体现的是一般与特殊的转化;数学归纳法体现的是一般与特殊、有限与无限的转化;反证法体现的是对立与统一的转化.
(1)请你推测g(5)能否用f(2),f(3),g(2),g(3)来表示;
(2)从(1)中的解能获得什么结论?能否将其推广?
[思路分析] 先将g(5)用f(2),f(3),g(2),g(3)表示出来,再推广到一般情况.专题五 ?转化与化归思想典例 6 『规律总结』 (1)归纳推理是从特殊到一般,从部分到整体的推理,在归纳、猜想阶段体现的是一般与特殊的相互转化关系.
(2)归纳推理得到的结论未必正确,还需检验和证明,有时要用到三段论.分类讨论思想在本章的证明问题中,无论是直接法还是间接法,都有所体现.如用反证法证明命题时,若结论的反面情况不唯一时,则必须采用分类讨论的方法对反面情况逐一否定,才能使问题得以证明.
已知平面上有四个点A,B,C,D,任何三点都不共线,求证以每三个点为顶点的三角形不可能都是锐角三角形.
[思路分析] 分别对第四个顶点在前三个顶点确定的三角形内、外两种情形进行讨论.专题六 ?分类讨论思想典例 7 [解析] 假设以每三个点为顶点的三角形都是锐角三角形,考虑点D在△ABC内、外两种情形.
①如图(1)所示,点D在△ABC内.
根据假设,围绕点D的三个角都是锐角,
从而得∠ADC+∠ADB+∠BDC<270°.
这与一个周角等于360°矛盾.②如图(2)所示,点D在△ABC外.
根据假设,在△ABD中,∠BAD<90°,
在△ABC中,∠ABC<90°,
在△BCD中,∠BCD<90°,
在△ADC中,∠ADC<90°,
从而有∠ABC+∠BCD+∠CDA+∠DAB<360°.
这与四边形ABCD的内角和为360°矛盾.
综合①②可知,假设不成立,故原结论成立.『规律总结』 利用反证法证明时,若否定结论后出现多种情况,则需要分类讨论,记得最后下结论时,说明上述情况均矛盾,故假设不成立,原结论成立.一、选择题
1.异面直线在同一平面内的射影不可能是( )
A.两条平行直线 B.两条相交直线
C.一点与一直线 D.同一条直线
[解析] 若两条直线在同一平面的射影是同一直线,则这两条直线的位置关系为平行或相交或重合,这均与异面矛盾,故异面直线在同一平面内的射影不可能为一条直线.故应选D.D 2.已知f(x)=x3+x,a,b,c∈R,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值一定( )
A.大于零 B.等于零
C.小于零 D.正负都可能
[解析] f(x)=x3+x是奇函数且在R上是增函数,
由a+b>0,得a>-b,故f(a)>f(-b).
可得f(a)+f(b)>0.
同理f(a)+f(c)>0,f(a)+f(c)>0.
所以f(a)+f(b)+f(c)>0.故选A.A 3.下列代数式(其中k∈N*)能被9整除的是( )
A.6+6·7k B.2+7k-1
C.2(2+7k+1) D.3(2+7k)
[解析] (1)当k=1时,显然只有3(2+7k)能被9整除.
(2)假设当k=n(n∈N*)时,命题成立,即3(2+7n)能被9整除,那么3(2+ 7n+1)=21(2+7n)-36.
∵3(2+7n)能被9整除,36能被9整除,
∴21(2+7n)-36能被9整除,
这就是说,k=n+1时命题也成立.
由(1)(2)可知,命题对任何k∈N*都成立.D 4.黑白两种颜色的正六边形地砖如图所示的规律拼成若干个图案:
则第n个图案中有白色地砖有( )
A.4n-2块 B.4n+2块
C.3n+3块 D.3n-3块
[解析] 第1个图案中有白色地砖6块,第2个图案中有白色地砖10块,第3个图案中有白色地砖14块,归纳为:第n个图案中有白色地砖(4n+2)块,故选B.B 二、填空题
5.根据下面一组等式
S1=1,
S2=2+3=5,
S3=4+5+6=15,
S4=7+8+9+10=34,
S5=11+12+13+14+15=65,
S6=16+17+18+19+20+21=111,
S7=22+23+24+25+26+27+28=175,
…
可得S1+S3+S5+…+S2n-1=____.n4 [解析] 根据所给等式组,不难看出:S1=1=14;
S1+S3=1+15=16=24;
S1+S3+S5=1+15+65=81=34,
S1+S3+S5+S7=1+15+65+175=256=44,
由此可得S1+S3+S5+…+S2n-1=n4.6.对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:“____________________ ________”,这个类比命题是_____命题(填“真”或“假”).
[解析] 类比推理要找两类事物的类似特征,平面几何中的线,可类比立体几何中的面.故可类比得出真命题“夹在两个平行平面间的平行线段相等”.夹在两个平行平面间的平行 线段相等 真
2.演绎推理
演绎推理是数学证明中的基本推理形式,“三段论”是演绎推理的一般模式.专题一 ?归纳与类比3.近几年高考对推理的考查:
(1)以选择题、填空题的形式考查合情推理;
(2)以选择题或解答题的形式考查演绎推理;
(3)题目难度不大,多以中低档题为主. 将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … … …
根据以上排列规律,数阵中第n(n≥3)行的从左至右的第3个数为_________.典例 1 在平面上,我们用一直线去截正方形的一个角,那么截下的一个直角三角形,按如图所标边长,由勾股定理有c2=a2+b2.设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1、S2、S3表示三个侧面面积,S表示截面面积,那么类比得到的结论是______________.典例 2 证明如下:如图,作OE⊥平面LMN,垂足为E,连接LE并延长交MN于F,
∵LO⊥OM,LO⊥ON,
∴LO⊥平面MON,
∵MN?平面MON,
∴LO⊥MN,『规律方法』 类比推理应从具体问题出发,通过观察、分析、类比、归纳而得出结论.通常情况下,平面图形的边长、面积往往类比空间几何体的面积、体积.综合与分析法是证明命题的两种最基本、最常用的直接证明方法.综合法常用于由已知推论较易找到思路时;分析法常用于条件复杂、思考方向不明确且用综合法较难证明时.单纯应用分析法证明并不多见,常常是用分析法寻找思路,用综合法表述过程.因此在实际应用中,经常要把综合法与分析法结合起来使用.本考点在高考中每年都要涉及,主要以考查直接证明中的综合法为主.专题二 ?直接证明 (2019·清水县期中)设a>0,b>0,2c>a+b,求证:
(1)c2>ab;
[思路分析] (1)根据基本不等式的证明即可证明c2>ab;
(2)利用分析法进行证明.典例 3 反证法是间接证明的一种基本方法,它不去直接证明结论,而是先否定结论,在否定结论的基础上,运用正确的推理,导出矛盾,从而肯定结论的真实性.在证明一些否定性命题、唯一性命题或含有“至多”“至少”等字样的命题时,正面证明往往较难,此时可考虑反证法,即“正难则反”.
设{an}是公比为q的等比数列.
(1)推导{an}的前n项和公式.
(2)设q≠1,证明:数列{an+1}不是等比数列.专题三 ?用反证法证明典例 4 [解析] (1)分两种情况讨论.
①当q=1时,数列{an}是首项为a1的常数数列,所以Sn=a1+a1+…+a1=na1.
②当q≠1时,Sn=a1+a2+…+an-1+an?qSn=qa1+qa2+…+qan-1+qan.
上面两式错位相减:
(1-q)Sn=a1+(a2-qa1)+(a3-qa2)+…+(an-qan-1)-qan=a1-qan(2)使用反证法.
设{an}是公比q≠1的等比数列,假设数列{an+1}是等比数列,则
(a2+1)2=(a1+1)(a3+1)即(a1q+1)2
=(a1+1)(a1q2+1),
整理得a1(q-1)2=0得a1=0或q=1均与题设矛盾,故数列{an+1}不是等比数列.『规律方法』 用反证法证明问题时要注意以下三点
(1)必须否定结论,即肯定结论的反面,当结论的反面呈现多样性时,必须罗列出各种可能结论,缺少任何一种可能,都不是反证法.
(2)反证法必须从否定结论进行推证,即应把结论的反面作为条件,且必须根据这一条件进行推证,否则,仅否定结论,不从结论的反面出发进行推理,就不是反证法.
(3)推导出的矛盾可能多种多样,有的与已知矛盾,有的与假设矛盾,有的与事实矛盾等,但是推导出的矛盾必须是明显的.数学归纳法是一种证明方法,可以证明与正整数有关的命题,如恒等式、不等式、几何问题以及整除问题等.高考数学归纳法的考查,一般以数列为背景,涉及等式、不等式等问题,归纳—猜想—证明是解决此问题的通法.
在数列{an}与{bn}中,a1=1,b1=4,数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0,2an+1为bn与bn+1的等比中项,n∈N*.
(1)求a2,b2的值;
(2)求数列{an}与{bn}的通项公式.专题四 ?用数学归纳法解题典例 5 『规律总结』 数学归纳法的主要思想:数学归纳法中两个步骤体现了递推思想,第一步是递推基础,也叫归纳奠基;第二步是递推的依据,也叫归纳递推.在这一步中归纳假设必须用上,否则就不是数学归纳法.转化与化归的思想方法是数学最基本的思想方法,数学中一切问题的解决都离不开转化与化归.转化与化归是数学思想方法的灵魂.在本章中,合情推理与演绎推理体现的是一般与特殊的转化;数学归纳法体现的是一般与特殊、有限与无限的转化;反证法体现的是对立与统一的转化.
(1)请你推测g(5)能否用f(2),f(3),g(2),g(3)来表示;
(2)从(1)中的解能获得什么结论?能否将其推广?
[思路分析] 先将g(5)用f(2),f(3),g(2),g(3)表示出来,再推广到一般情况.专题五 ?转化与化归思想典例 6 『规律总结』 (1)归纳推理是从特殊到一般,从部分到整体的推理,在归纳、猜想阶段体现的是一般与特殊的相互转化关系.
(2)归纳推理得到的结论未必正确,还需检验和证明,有时要用到三段论.分类讨论思想在本章的证明问题中,无论是直接法还是间接法,都有所体现.如用反证法证明命题时,若结论的反面情况不唯一时,则必须采用分类讨论的方法对反面情况逐一否定,才能使问题得以证明.
已知平面上有四个点A,B,C,D,任何三点都不共线,求证以每三个点为顶点的三角形不可能都是锐角三角形.
[思路分析] 分别对第四个顶点在前三个顶点确定的三角形内、外两种情形进行讨论.专题六 ?分类讨论思想典例 7 [解析] 假设以每三个点为顶点的三角形都是锐角三角形,考虑点D在△ABC内、外两种情形.
①如图(1)所示,点D在△ABC内.
根据假设,围绕点D的三个角都是锐角,
从而得∠ADC+∠ADB+∠BDC<270°.
这与一个周角等于360°矛盾.②如图(2)所示,点D在△ABC外.
根据假设,在△ABD中,∠BAD<90°,
在△ABC中,∠ABC<90°,
在△BCD中,∠BCD<90°,
在△ADC中,∠ADC<90°,
从而有∠ABC+∠BCD+∠CDA+∠DAB<360°.
这与四边形ABCD的内角和为360°矛盾.
综合①②可知,假设不成立,故原结论成立.『规律总结』 利用反证法证明时,若否定结论后出现多种情况,则需要分类讨论,记得最后下结论时,说明上述情况均矛盾,故假设不成立,原结论成立.一、选择题
1.异面直线在同一平面内的射影不可能是( )
A.两条平行直线 B.两条相交直线
C.一点与一直线 D.同一条直线
[解析] 若两条直线在同一平面的射影是同一直线,则这两条直线的位置关系为平行或相交或重合,这均与异面矛盾,故异面直线在同一平面内的射影不可能为一条直线.故应选D.D 2.已知f(x)=x3+x,a,b,c∈R,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值一定( )
A.大于零 B.等于零
C.小于零 D.正负都可能
[解析] f(x)=x3+x是奇函数且在R上是增函数,
由a+b>0,得a>-b,故f(a)>f(-b).
可得f(a)+f(b)>0.
同理f(a)+f(c)>0,f(a)+f(c)>0.
所以f(a)+f(b)+f(c)>0.故选A.A 3.下列代数式(其中k∈N*)能被9整除的是( )
A.6+6·7k B.2+7k-1
C.2(2+7k+1) D.3(2+7k)
[解析] (1)当k=1时,显然只有3(2+7k)能被9整除.
(2)假设当k=n(n∈N*)时,命题成立,即3(2+7n)能被9整除,那么3(2+ 7n+1)=21(2+7n)-36.
∵3(2+7n)能被9整除,36能被9整除,
∴21(2+7n)-36能被9整除,
这就是说,k=n+1时命题也成立.
由(1)(2)可知,命题对任何k∈N*都成立.D 4.黑白两种颜色的正六边形地砖如图所示的规律拼成若干个图案:
则第n个图案中有白色地砖有( )
A.4n-2块 B.4n+2块
C.3n+3块 D.3n-3块
[解析] 第1个图案中有白色地砖6块,第2个图案中有白色地砖10块,第3个图案中有白色地砖14块,归纳为:第n个图案中有白色地砖(4n+2)块,故选B.B 二、填空题
5.根据下面一组等式
S1=1,
S2=2+3=5,
S3=4+5+6=15,
S4=7+8+9+10=34,
S5=11+12+13+14+15=65,
S6=16+17+18+19+20+21=111,
S7=22+23+24+25+26+27+28=175,
…
可得S1+S3+S5+…+S2n-1=____.n4 [解析] 根据所给等式组,不难看出:S1=1=14;
S1+S3=1+15=16=24;
S1+S3+S5=1+15+65=81=34,
S1+S3+S5+S7=1+15+65+175=256=44,
由此可得S1+S3+S5+…+S2n-1=n4.6.对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:“____________________ ________”,这个类比命题是_____命题(填“真”或“假”).
[解析] 类比推理要找两类事物的类似特征,平面几何中的线,可类比立体几何中的面.故可类比得出真命题“夹在两个平行平面间的平行线段相等”.夹在两个平行平面间的平行 线段相等 真
同课章节目录
