2019-2020学年高中北师大版数学选修1-2第一章统计案例1第2课时§1 回归分析课件:52张PPT
文档属性
| 名称 | 2019-2020学年高中北师大版数学选修1-2第一章统计案例1第2课时§1 回归分析课件:52张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 860.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 16:03:22 | ||
图片预览









文档简介
课件52张PPT。第一章统计案例§1 回归分析第2课时 可线性化的回归分析自主预习学案对于两变量之间非线性相关是否能用直线来拟合?有什么弊端?1.非线性回归问题
(1)在实际问题中,当变量之间不是线性相关关系时,不能用线性回归方程描述它们之间的相关关系,需要进行非线性回归分析.在具体问题中,我们首先应该作出原始数据(x,y)的__________,从__________中看出数据的大致规律,再根据这个规律选择适当的函数进行拟合.
(2)可线性化的回归分析:非线性回归问题的非线性回归方程一般很难求,因此把非线性回归化为线性回归是解决问题的好方法:把非线性回归化为____________,再利用线性回归的方法确定参数a及b的估计值.散点图 散点图 线性回归 2.非线性回归问题
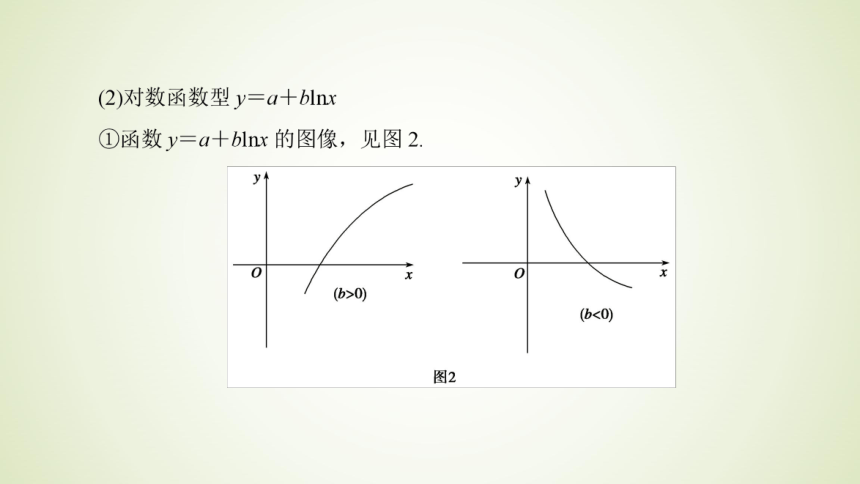
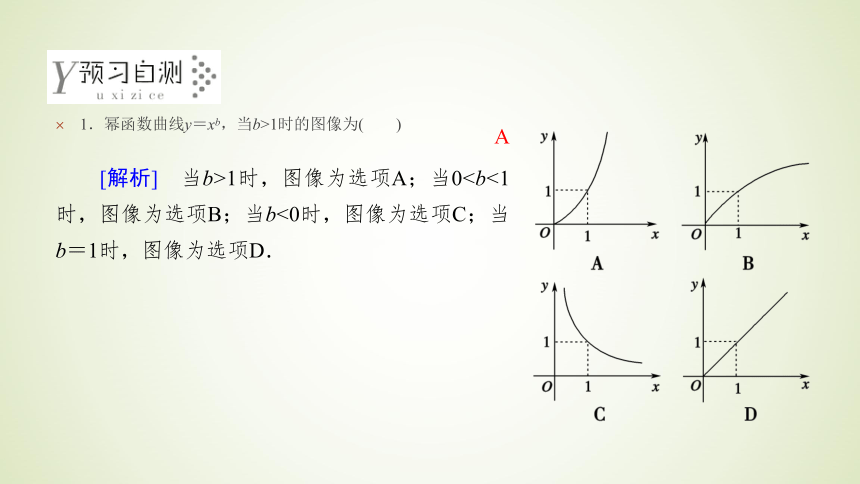
在大量的实际问题中,研究的两个变量不一定呈线性相关关系,它们之间可能呈指数关系或对数关系.在某些情况下可以借助线性回归模型研究呈非线性关系的两个变量之间的关系.非线性回归问题的解题方法是:(1)若问题中已经给出公式,则可通过变换,将变量的非线性关系转化为线性关系,将问题转化为线性回归问题来解决;(2)若问题中没有给出公式,需要我们画出已知数据的散点图,通过与各种函数(如指数函数、对数函数、幂函数等)的图像做比较,选择一种与这些散点拟合的最好的函数,然后采用适当的变量变换,将问题转化为线性回归分析问题.1.幂函数曲线y=xb,当b>1时的图像为( )A[解析] 当b>1时,图像为选项A;当0[解析] ∵y=3e-2x,∴y>0,排除A、C,又x∈R,排除D.B3.某地今年上半年患某种传染病的人数y(人)与月份x(月)之间满足函数关系,模型为y=aebx,确定这个函数解析式__________________.y=e3.911 58+0.09x 互动探究学案命题方向1 ?给定函数模型,求回归方程若y与t之间满足y=aebt关系,求函数解析式,若按此增长趋势,估计大约在哪一年我国人口达到14亿?
[思路分析] 函数模型为指数函数,可转化为线性相关关系,从而求出.
[解析] 设μ=lny,c=lna,则μ=c+bt.『规律方法』 已知曲线类型进行回归分析的步骤:
(1)将非线性函数通过变量代换转化为线性函数.
(2)将所给数据点加以转换.
(3)按最小二乘法原理求线性回归方程并进行检验.
(4)将线性回归方程转换为关于原始变量x、y的回归方程.
(5)依据回归方程作出预报.命题方向2 ?函数模型的选取『规律方法』 实际问题中非线性相关的函数模型的选取
1.采集数据、画出散点图;
2.根据散点图中点的分布状态选取所有可能的函数类型;
3.作变量代换,将函数转化为线性函数;
4.作出线性相关的散点图,或计算线性相关系数r,通过比较选定函数模型;
5.求回归直线方程,并检查;
6.作出预报.〔跟踪练习2〕
为了研究某种细菌繁殖的个数随时间x变化的情况,收集数据如下:
(1)用天数作为解释变量,繁殖个数作为预报变量,作出这些数据的散点图;
(2)描述解释变量与预报变量之间的关系.[解析] (1)作出散点图如图所示.[辨析] 上述解答过程没有作出散点图(或求相关系数r)进行判断,就直接求回归直线方程导致错误.由散点图(如图2)也可以看出,这些点基本上分布在一条直线附近,可以认为y与t具有线性相关关系,列表如下:可线性化的回归分析 (3)分析模型的拟合效果
对于同一问题可以有几种不同的拟合模型,对于给定的样本点(x1,y1),(x1,y2),…,(xn,yn),可以通过以下几种方式确定选用哪种模型更合适.
①可以根据转换后的对应数据作散点图来确定线性回归的拟合情况,判断使用哪一种曲线模型较为合适.
②可以通过原始数据及y和x之间的非线性回归方程列出残差对比分析表,一般通过残差平方和比较两种模型的拟合效果,其中残差平方和较小的拟合效果较好.
③还可以用R2来比较模型的拟合效果,R2越大(越接近1),拟合效果越好.[解析] 根据收集的数据作散点图如图.
根据样本点的分布情况,可选用指数型函数模型y=c1ec2x(c1,c2为待定的参数),
令z=lny,则z=c2x+lnc1,即变换后样本点应该分布在直线z=bx+a(a=lnc1,b=c2)的附近,由y与x的数据表得z与x的数据表如下:
作出z与x的散点图如图『规律方法』 解决非线性回归问题的具体做法是:(1)若问题中已给出经验公式,可以将解释变量进行变换(换元),将变量的非线性关系转化为线性关系,将问题转化为线性回归分析问题解决.(2)若问题中没有给出经验公式,需要画出已知数据的散点图,通过与各种函数(指数函数、对数函数、幂函数等)的图像做比较,选择与这些散点拟合最好的函数,然后采用适当的变量变换,将问题转化为线性回归问题解决.1.下列说法错误的是( )
A.当变量之间的相关关系不是线性相关关系时,也能直接用线性回归方程描述它们之间的相关关系
B.把非线性回归化线性回归为我们解决问题提供一种方法
C.当变量之间的相关关系不是线性相关关系时,也能描述变量之间的相关关系
D.当变量之间的相关关系不是线性相关关系时,可以通过适当的变换使其转换为线性关系,将问题化为线性回归分析问题来解决
[解析] 此题考查解决线性相关问题的基本思路.A2.下表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是y=-0.7x+a,则a等于( )
A.10.5 B.5.15
C.5.2 D.5.25D3.在某种新型材料的研制中,试验人员获得了下列一组试验数据,现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
[解析] 作散点图,从图中观察可知,应为对数函数模型.B
(1)在实际问题中,当变量之间不是线性相关关系时,不能用线性回归方程描述它们之间的相关关系,需要进行非线性回归分析.在具体问题中,我们首先应该作出原始数据(x,y)的__________,从__________中看出数据的大致规律,再根据这个规律选择适当的函数进行拟合.
(2)可线性化的回归分析:非线性回归问题的非线性回归方程一般很难求,因此把非线性回归化为线性回归是解决问题的好方法:把非线性回归化为____________,再利用线性回归的方法确定参数a及b的估计值.散点图 散点图 线性回归 2.非线性回归问题
在大量的实际问题中,研究的两个变量不一定呈线性相关关系,它们之间可能呈指数关系或对数关系.在某些情况下可以借助线性回归模型研究呈非线性关系的两个变量之间的关系.非线性回归问题的解题方法是:(1)若问题中已经给出公式,则可通过变换,将变量的非线性关系转化为线性关系,将问题转化为线性回归问题来解决;(2)若问题中没有给出公式,需要我们画出已知数据的散点图,通过与各种函数(如指数函数、对数函数、幂函数等)的图像做比较,选择一种与这些散点拟合的最好的函数,然后采用适当的变量变换,将问题转化为线性回归分析问题.1.幂函数曲线y=xb,当b>1时的图像为( )A[解析] 当b>1时,图像为选项A;当0
[思路分析] 函数模型为指数函数,可转化为线性相关关系,从而求出.
[解析] 设μ=lny,c=lna,则μ=c+bt.『规律方法』 已知曲线类型进行回归分析的步骤:
(1)将非线性函数通过变量代换转化为线性函数.
(2)将所给数据点加以转换.
(3)按最小二乘法原理求线性回归方程并进行检验.
(4)将线性回归方程转换为关于原始变量x、y的回归方程.
(5)依据回归方程作出预报.命题方向2 ?函数模型的选取『规律方法』 实际问题中非线性相关的函数模型的选取
1.采集数据、画出散点图;
2.根据散点图中点的分布状态选取所有可能的函数类型;
3.作变量代换,将函数转化为线性函数;
4.作出线性相关的散点图,或计算线性相关系数r,通过比较选定函数模型;
5.求回归直线方程,并检查;
6.作出预报.〔跟踪练习2〕
为了研究某种细菌繁殖的个数随时间x变化的情况,收集数据如下:
(1)用天数作为解释变量,繁殖个数作为预报变量,作出这些数据的散点图;
(2)描述解释变量与预报变量之间的关系.[解析] (1)作出散点图如图所示.[辨析] 上述解答过程没有作出散点图(或求相关系数r)进行判断,就直接求回归直线方程导致错误.由散点图(如图2)也可以看出,这些点基本上分布在一条直线附近,可以认为y与t具有线性相关关系,列表如下:可线性化的回归分析 (3)分析模型的拟合效果
对于同一问题可以有几种不同的拟合模型,对于给定的样本点(x1,y1),(x1,y2),…,(xn,yn),可以通过以下几种方式确定选用哪种模型更合适.
①可以根据转换后的对应数据作散点图来确定线性回归的拟合情况,判断使用哪一种曲线模型较为合适.
②可以通过原始数据及y和x之间的非线性回归方程列出残差对比分析表,一般通过残差平方和比较两种模型的拟合效果,其中残差平方和较小的拟合效果较好.
③还可以用R2来比较模型的拟合效果,R2越大(越接近1),拟合效果越好.[解析] 根据收集的数据作散点图如图.
根据样本点的分布情况,可选用指数型函数模型y=c1ec2x(c1,c2为待定的参数),
令z=lny,则z=c2x+lnc1,即变换后样本点应该分布在直线z=bx+a(a=lnc1,b=c2)的附近,由y与x的数据表得z与x的数据表如下:
作出z与x的散点图如图『规律方法』 解决非线性回归问题的具体做法是:(1)若问题中已给出经验公式,可以将解释变量进行变换(换元),将变量的非线性关系转化为线性关系,将问题转化为线性回归分析问题解决.(2)若问题中没有给出经验公式,需要画出已知数据的散点图,通过与各种函数(指数函数、对数函数、幂函数等)的图像做比较,选择与这些散点拟合最好的函数,然后采用适当的变量变换,将问题转化为线性回归问题解决.1.下列说法错误的是( )
A.当变量之间的相关关系不是线性相关关系时,也能直接用线性回归方程描述它们之间的相关关系
B.把非线性回归化线性回归为我们解决问题提供一种方法
C.当变量之间的相关关系不是线性相关关系时,也能描述变量之间的相关关系
D.当变量之间的相关关系不是线性相关关系时,可以通过适当的变换使其转换为线性关系,将问题化为线性回归分析问题来解决
[解析] 此题考查解决线性相关问题的基本思路.A2.下表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是y=-0.7x+a,则a等于( )
A.10.5 B.5.15
C.5.2 D.5.25D3.在某种新型材料的研制中,试验人员获得了下列一组试验数据,现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
[解析] 作散点图,从图中观察可知,应为对数函数模型.B
同课章节目录
