四年级下册数学教案-10.2 图形与几何
文档属性
| 名称 | 四年级下册数学教案-10.2 图形与几何 |  | |
| 格式 | zip | ||
| 文件大小 | 165.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 20:18:30 | ||
图片预览


文档简介
第十单元 总 复 习
第2课时 图形与几何
知识板块
要点梳理
具体内容
观察物体
观察物体
1.从不同方向观察同一立体图形得到的平面图形:同一个立体图形,观察的角度不同,所看到的平面图形也不同;观察的角度不同,所看到的平面图形也可能相同。
2.不同的立体图形,从不同的位置观察得到的平面图形:辨认从相同方向观察拼摆的不同的立体图形,得到的平面图形,可能是相同的,也可能是不同的。
图形的运动
轴对称
1. 轴对称的意义:一个图形沿着一条直线对折,直线两边的部分能够完全重合,那么这个图形叫作轴对称图形。折痕所在的这条直线叫作对称轴。
2. 轴对称的性质:对应点到对称轴的距离相等,对应点的连线垂直对称轴。
3.轴对称的特征:对称轴两侧的图形能够完全重合。
平移
1.平移的意义:物体或图形在直线方向上移动,而本身没有发生方向上的改变,就可以近似看作是平移现象。
2.平移的基本性质:物体或图形沿直线移动,本身形状的大小和方向不发生改变。
三角形
三角形的特性
1.三角形的意义:由3条线段围成的图形(每相邻两条线段的端点相连)叫作三角形。
2.三角形的高和底:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高。这条对边叫作三角形的底。
3.三角形的特性:三角形具有稳定性。
4.三角形的特征:三角形有三条边,三个角,三个顶点。
5.两点间的距离:两点间的所有连线中线段最短,这条线段的长度叫作两点间的距离。
6.三角形三边的关系:三角形任意两边之和大于第三边。
知识板块
要点梳理
具体内容
三角形的分类
1.按角分:锐角三角形,直角三角形,钝角三角形。
三个角都是锐角的三角形叫作锐角三角形;
有一个角是直角的三角形是直角三角形;
有一个角是钝角的三角形叫作钝角三角形。
2.按边分:等腰三角形和等边三角形。
有两条边相等的三角形叫作等腰三角形;
三条边相等的三角形叫作等边三角形(正三角形)。
3.特殊的三角形:
等腰三角形的两腰相等,两个底角相等;
等边三角形的三条边相等,三个角相等。
等边三角形是特殊的等腰三角形。
三角形的内角和
1.三角形的内角和:三角形的内角和是180°。
2.四边形的内角和:四边形的内角和是360°。
教材知识荟
【考点一】观察物体
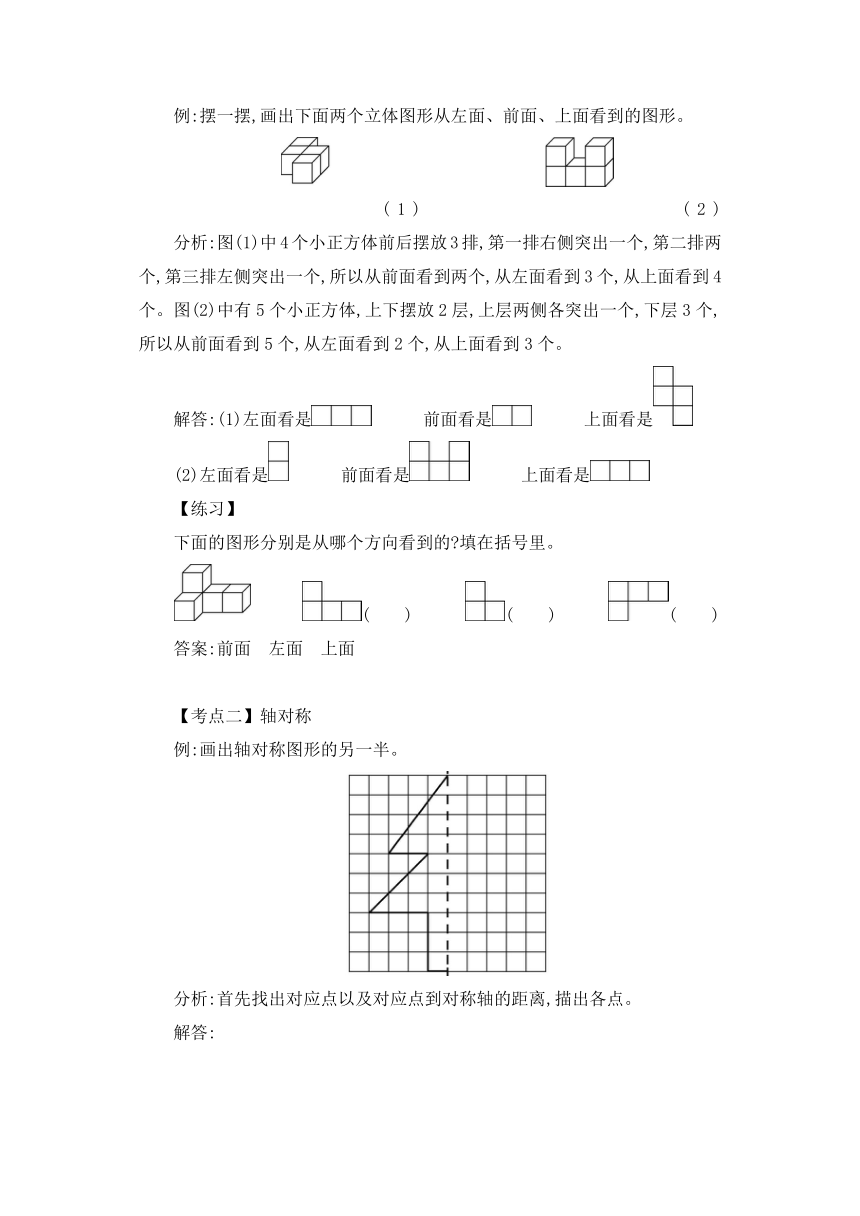
例:摆一摆,画出下面两个立体图形从左面、前面、上面看到的图形。
( 1 ) ( 2 )
分析:图(1)中4个小正方体前后摆放3排,第一排右侧突出一个,第二排两个,第三排左侧突出一个,所以从前面看到两个,从左面看到3个,从上面看到4个。图(2)中有5个小正方体,上下摆放2层,上层两侧各突出一个,下层3个,所以从前面看到5个,从左面看到2个,从上面看到3个。
解答:(1)左面看是 前面看是 上面看是
(2)左面看是 前面看是 上面看是
【练习】
下面的图形分别是从哪个方向看到的?填在括号里。
( ) ( ) ( )
答案:前面 左面 上面
【考点二】轴对称
例:画出轴对称图形的另一半。
分析:首先找出对应点以及对应点到对称轴的距离,描出各点。
解答:
【练习】
根据轴对称和平移画出美丽的图案。
答案:
【考点三】三角形
例1:(1)判断:用三条线段肯定能围成一个三角形。( )
每个三角形中至少有一个锐角。( )
有一个角是锐角的三角形是锐角三角形。( )
(2)选择:一个三角形只有两个锐角,那么这个三角形是一个( )三角形。
A.钝角 B.直角 C.钝角或直角
分析:(1)根据三角形的特点进行判断。
(2)锐角三角形有三个锐角,而钝角三角形和直角三角形都有两个锐角,由此判断有两种可能性。
解答:(1)× × × (2)C
例2:你能用下面的4根小棒中的任意3根组成三角形吗?选择的是哪3根?
分析:根据三角形任意两边之和大于第三边,可以选择长10 cm、8 cm、6 cm的3根小棒组成三角形,也可以选择长8 cm、6 cm、4 cm的3根小棒组成三角形。(选择方法不唯一)
解答:选择的3根小棒是:10 cm、 8 cm、6 cm或8 cm、6 cm、4 cm。
例3:(1)在能组成三角形的三个角后面的括号里画“√”,不能组成三角形的画“×”。
40°、45°、70°( ) 60°、50°、60° ( ) 80°、20°、80°( )
(2)三角形的一个角是50° ,另一角是70°,第三个角是( ),这个三角形是( )三角形。
分析:(1)根据三角形的内角和是180°进行判断。
(2)根据三角形的内角和判断第三个角是180°-50°-70°=60°,三个角都是锐角,因此是锐角三角形。
解答:(1)× × √ (2)60° 锐角
【练习】
1.三角形ABC中,若∠A=35°,∠B=65°,则∠C是多少度?若∠A=120°,∠B=2∠C,则∠C是多少度?
答案:180°-(35°+65°)=80° ( 180°-120°)÷3=20°
2.在等腰三角形中,已知顶角是50°,则底角是多少度?
答案:(180°-50°)÷2=65°
3.根据下图求出∠2和∠3各是多少度。(∠1=60°, ∠4=125°)
答案:∠2=65° ∠3=55°
我的反思:
?
?
?
?
?
?
?
?
第2课时 图形与几何
知识板块
要点梳理
具体内容
观察物体
观察物体
1.从不同方向观察同一立体图形得到的平面图形:同一个立体图形,观察的角度不同,所看到的平面图形也不同;观察的角度不同,所看到的平面图形也可能相同。
2.不同的立体图形,从不同的位置观察得到的平面图形:辨认从相同方向观察拼摆的不同的立体图形,得到的平面图形,可能是相同的,也可能是不同的。
图形的运动
轴对称
1. 轴对称的意义:一个图形沿着一条直线对折,直线两边的部分能够完全重合,那么这个图形叫作轴对称图形。折痕所在的这条直线叫作对称轴。
2. 轴对称的性质:对应点到对称轴的距离相等,对应点的连线垂直对称轴。
3.轴对称的特征:对称轴两侧的图形能够完全重合。
平移
1.平移的意义:物体或图形在直线方向上移动,而本身没有发生方向上的改变,就可以近似看作是平移现象。
2.平移的基本性质:物体或图形沿直线移动,本身形状的大小和方向不发生改变。
三角形
三角形的特性
1.三角形的意义:由3条线段围成的图形(每相邻两条线段的端点相连)叫作三角形。
2.三角形的高和底:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高。这条对边叫作三角形的底。
3.三角形的特性:三角形具有稳定性。
4.三角形的特征:三角形有三条边,三个角,三个顶点。
5.两点间的距离:两点间的所有连线中线段最短,这条线段的长度叫作两点间的距离。
6.三角形三边的关系:三角形任意两边之和大于第三边。
知识板块
要点梳理
具体内容
三角形的分类
1.按角分:锐角三角形,直角三角形,钝角三角形。
三个角都是锐角的三角形叫作锐角三角形;
有一个角是直角的三角形是直角三角形;
有一个角是钝角的三角形叫作钝角三角形。
2.按边分:等腰三角形和等边三角形。
有两条边相等的三角形叫作等腰三角形;
三条边相等的三角形叫作等边三角形(正三角形)。
3.特殊的三角形:
等腰三角形的两腰相等,两个底角相等;
等边三角形的三条边相等,三个角相等。
等边三角形是特殊的等腰三角形。
三角形的内角和
1.三角形的内角和:三角形的内角和是180°。
2.四边形的内角和:四边形的内角和是360°。
教材知识荟
【考点一】观察物体
例:摆一摆,画出下面两个立体图形从左面、前面、上面看到的图形。
( 1 ) ( 2 )
分析:图(1)中4个小正方体前后摆放3排,第一排右侧突出一个,第二排两个,第三排左侧突出一个,所以从前面看到两个,从左面看到3个,从上面看到4个。图(2)中有5个小正方体,上下摆放2层,上层两侧各突出一个,下层3个,所以从前面看到5个,从左面看到2个,从上面看到3个。
解答:(1)左面看是 前面看是 上面看是
(2)左面看是 前面看是 上面看是
【练习】
下面的图形分别是从哪个方向看到的?填在括号里。
( ) ( ) ( )
答案:前面 左面 上面
【考点二】轴对称
例:画出轴对称图形的另一半。
分析:首先找出对应点以及对应点到对称轴的距离,描出各点。
解答:
【练习】
根据轴对称和平移画出美丽的图案。
答案:
【考点三】三角形
例1:(1)判断:用三条线段肯定能围成一个三角形。( )
每个三角形中至少有一个锐角。( )
有一个角是锐角的三角形是锐角三角形。( )
(2)选择:一个三角形只有两个锐角,那么这个三角形是一个( )三角形。
A.钝角 B.直角 C.钝角或直角
分析:(1)根据三角形的特点进行判断。
(2)锐角三角形有三个锐角,而钝角三角形和直角三角形都有两个锐角,由此判断有两种可能性。
解答:(1)× × × (2)C
例2:你能用下面的4根小棒中的任意3根组成三角形吗?选择的是哪3根?
分析:根据三角形任意两边之和大于第三边,可以选择长10 cm、8 cm、6 cm的3根小棒组成三角形,也可以选择长8 cm、6 cm、4 cm的3根小棒组成三角形。(选择方法不唯一)
解答:选择的3根小棒是:10 cm、 8 cm、6 cm或8 cm、6 cm、4 cm。
例3:(1)在能组成三角形的三个角后面的括号里画“√”,不能组成三角形的画“×”。
40°、45°、70°( ) 60°、50°、60° ( ) 80°、20°、80°( )
(2)三角形的一个角是50° ,另一角是70°,第三个角是( ),这个三角形是( )三角形。
分析:(1)根据三角形的内角和是180°进行判断。
(2)根据三角形的内角和判断第三个角是180°-50°-70°=60°,三个角都是锐角,因此是锐角三角形。
解答:(1)× × √ (2)60° 锐角
【练习】
1.三角形ABC中,若∠A=35°,∠B=65°,则∠C是多少度?若∠A=120°,∠B=2∠C,则∠C是多少度?
答案:180°-(35°+65°)=80° ( 180°-120°)÷3=20°
2.在等腰三角形中,已知顶角是50°,则底角是多少度?
答案:(180°-50°)÷2=65°
3.根据下图求出∠2和∠3各是多少度。(∠1=60°, ∠4=125°)
答案:∠2=65° ∠3=55°
我的反思:
?
?
?
?
?
?
?
?
