人教版数学四下5.5 多边形的内角和 课件(16张ppt)
文档属性
| 名称 | 人教版数学四下5.5 多边形的内角和 课件(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 16:14:31 | ||
图片预览



文档简介
(共17张PPT)
数学四年级
下册
第5单元
三角形
第5课时 多边形的内角和
一、复习导入
你们知道四边形的内角和是多少度吗?今天我们就来学习四边形的内角和知识和三角形的有关知识。
三角形的内角和是多少度?
二、探究新知
我们已知正方形和长方形的四个角都是直角,它们的内角和为360°,那么任意四边形的内角和是多少度?
(1)测量法两处任意一个四边形每个内角度数,然后相加为360°。
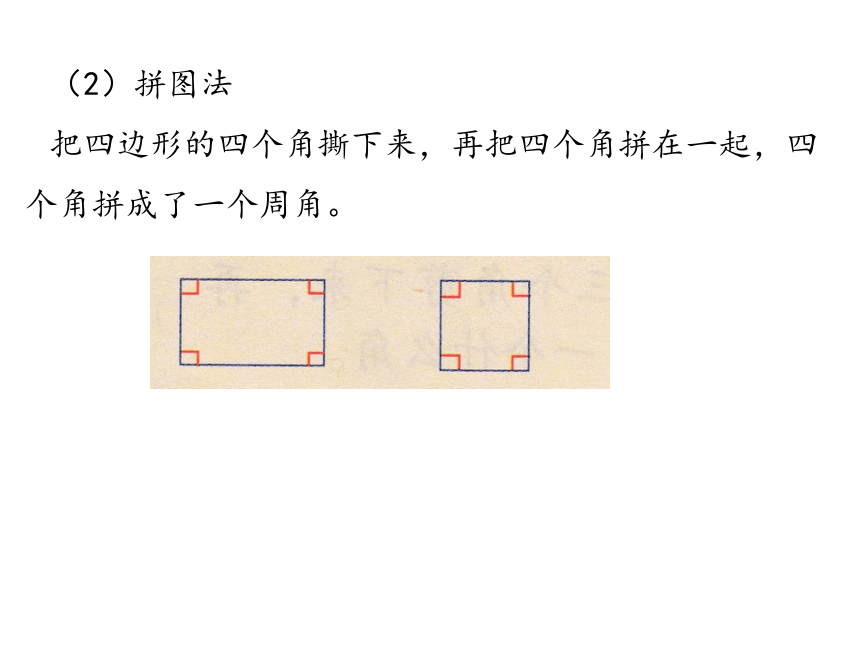
(2)拼图法
把四边形的四个角撕下来,再把四个角拼在一起,四个角拼成了一个周角。
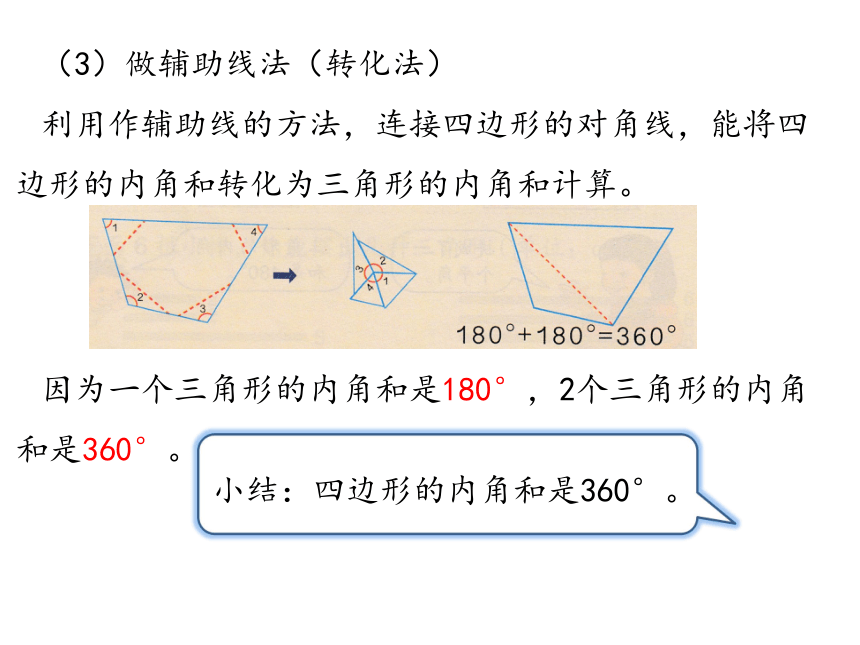
(3)做辅助线法(转化法)
利用作辅助线的方法,连接四边形的对角线,能将四边形的内角和转化为三角形的内角和计算。
小结:四边形的内角和是360°。
因为一个三角形的内角和是180°,2个三角形的内角和是360°。
能否类比四边形的方式解决五边形、六边形的内角和吗?
①把五边形分成三个三角形,3×180°=540°。
②把五边形分成一个三角形和一个四边形,
180°+360°=540°。
2. 探索五边形、六边形的内角和。
2. 探索多边形的内角和。
(1)多边形的内角和与三角形内角和有什么关系?
(2)多边形的边数与内角和有什么关系?
(3)从多边形的一个顶点引到对角线分成三角形的个数与多边形的边数有什么关系?
三角形的内角和:
四边形的内角和:
五边形的内角和:
六边形的内角和:
小结:从n边形的一个顶点出发,可以引(n-3)条对角线,将n边形分成(n-2)个三角形,则n边形的内角和为(n-2)×180°。
(3-2)×180°
(4-2)×180°
(5-2)×180°
(6-2)×180°
三、巩固练习
做一做
你能想办法求出右边这个多边形的内角和吗?
180°×4=720°
2.画一画,算一算,你发现了什么?
6
7
180°×4
180°×5
2
3
3.猜一猜。
在三角形中,一个是直角,另两个可能各是多少度?
在三角形两条边分别是3cm和4cm,另一条边可能是多少厘米?
在三角形中,一个是直角,另两个可能各是多少度?
(1)180-90=90(度)
答: (1)另两个角可能各是40度和50度。
90度=40度+50度
(2)3+4=7(厘米)
答: (2)另一条边可能是2厘米,3厘米,4厘米,5厘米,或者6厘米。
1厘米<2厘米<3厘米<4厘米<5厘米<6厘米<7厘米
4-3=1(厘米)
在三角形两条边分别是3cm和4cm,另一条边可能是多少厘米?
4.下面图形中各有个三角形?有什么规律?
图一有1个三角形;图二有3个三角形1+2=3(个);图三有6个三角形1+2+3=6(个);图四有10个三角形1+2+3+4=10(个)。
答:图一有1个三角形,图二有3个三角形,图三有6个三角形,图四有10个三角形。第几个图形的三角形的个数等于从1到几的连续的自然数的相加。
四、课堂小结
通过今天的学习,你有什么收获?
五、布置作业
有一个直角,有两条边相等。
只有两个锐角,没有直角。
三个角相等。
没有直角和钝角。
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
数学四年级
下册
第5单元
三角形
第5课时 多边形的内角和
一、复习导入
你们知道四边形的内角和是多少度吗?今天我们就来学习四边形的内角和知识和三角形的有关知识。
三角形的内角和是多少度?
二、探究新知
我们已知正方形和长方形的四个角都是直角,它们的内角和为360°,那么任意四边形的内角和是多少度?
(1)测量法两处任意一个四边形每个内角度数,然后相加为360°。
(2)拼图法
把四边形的四个角撕下来,再把四个角拼在一起,四个角拼成了一个周角。
(3)做辅助线法(转化法)
利用作辅助线的方法,连接四边形的对角线,能将四边形的内角和转化为三角形的内角和计算。
小结:四边形的内角和是360°。
因为一个三角形的内角和是180°,2个三角形的内角和是360°。
能否类比四边形的方式解决五边形、六边形的内角和吗?
①把五边形分成三个三角形,3×180°=540°。
②把五边形分成一个三角形和一个四边形,
180°+360°=540°。
2. 探索五边形、六边形的内角和。
2. 探索多边形的内角和。
(1)多边形的内角和与三角形内角和有什么关系?
(2)多边形的边数与内角和有什么关系?
(3)从多边形的一个顶点引到对角线分成三角形的个数与多边形的边数有什么关系?
三角形的内角和:
四边形的内角和:
五边形的内角和:
六边形的内角和:
小结:从n边形的一个顶点出发,可以引(n-3)条对角线,将n边形分成(n-2)个三角形,则n边形的内角和为(n-2)×180°。
(3-2)×180°
(4-2)×180°
(5-2)×180°
(6-2)×180°
三、巩固练习
做一做
你能想办法求出右边这个多边形的内角和吗?
180°×4=720°
2.画一画,算一算,你发现了什么?
6
7
180°×4
180°×5
2
3
3.猜一猜。
在三角形中,一个是直角,另两个可能各是多少度?
在三角形两条边分别是3cm和4cm,另一条边可能是多少厘米?
在三角形中,一个是直角,另两个可能各是多少度?
(1)180-90=90(度)
答: (1)另两个角可能各是40度和50度。
90度=40度+50度
(2)3+4=7(厘米)
答: (2)另一条边可能是2厘米,3厘米,4厘米,5厘米,或者6厘米。
1厘米<2厘米<3厘米<4厘米<5厘米<6厘米<7厘米
4-3=1(厘米)
在三角形两条边分别是3cm和4cm,另一条边可能是多少厘米?
4.下面图形中各有个三角形?有什么规律?
图一有1个三角形;图二有3个三角形1+2=3(个);图三有6个三角形1+2+3=6(个);图四有10个三角形1+2+3+4=10(个)。
答:图一有1个三角形,图二有3个三角形,图三有6个三角形,图四有10个三角形。第几个图形的三角形的个数等于从1到几的连续的自然数的相加。
四、课堂小结
通过今天的学习,你有什么收获?
五、布置作业
有一个直角,有两条边相等。
只有两个锐角,没有直角。
三个角相等。
没有直角和钝角。
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
