五年级下册科学课件-3.6 摆的研究| 教科版 (共17张PPT)
文档属性
| 名称 | 五年级下册科学课件-3.6 摆的研究| 教科版 (共17张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2020-02-02 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
6摆的研究
伽利略的故事
1582年的一天,伽利略到教堂作礼拜.一位修理工人不经意触动了教堂中的大吊灯,使它来回摆动.伽利略观察着,脑海里闪出测量吊灯摆动时间的念头.起初,吊灯在一个大圆弧上摆动,摆动速度较大,伽利略测算来回摆动一次的时间.后来,吊灯摆动的幅度变小了,摆动速度也变慢了,他又测量了来回摆动一次的时间.他大吃一惊,两次测量的时间是相同的.伽利略继续测量,直到吊灯几乎停止摆动.伽利略发现:吊灯来回摆动一次需要的时间与摆动幅度的大小无关,无论摆幅大小如何,来回摆动一次所需时间是相同的.即吊灯的摆动具有等时性,这就是伽利略最初的发现.
伽利略发现摆的故事
伽利略发现摆的故事
他被吊灯摆动的节律性吸引住了
——— 观察
每摆动一次的时间相等吗?摆幅大些,每摆动一次的时间还相等吗?
———— 提出疑问和假设
伽利略模仿吊灯进行实验,研究摆的特点
——— 实验探究
摆的等时性原理
———— 分析得出结论
生活中的摆——摆的应用
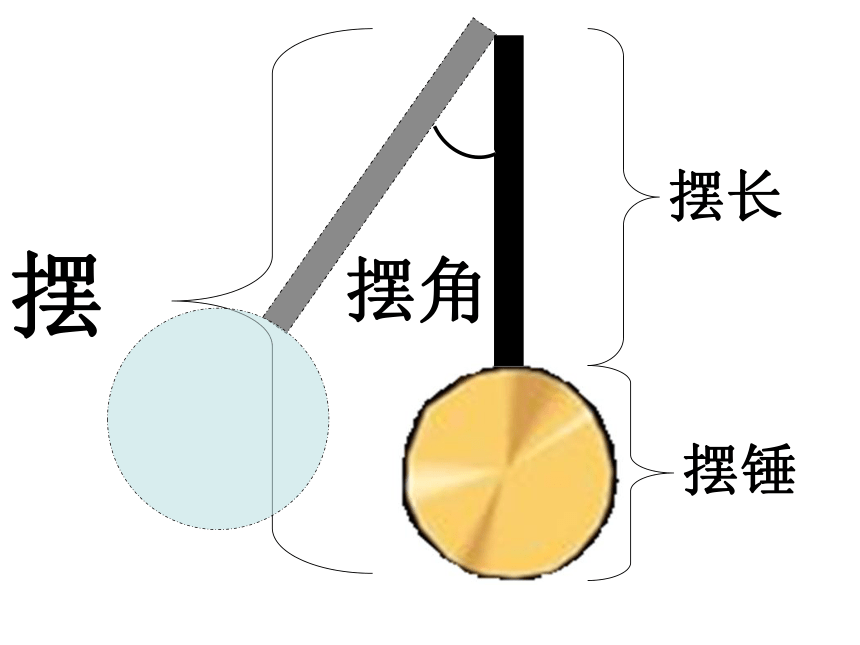
摆长
摆锤
摆
摆角
1、我们的假设:摆的摆动快慢与 有关。
2、我们的猜测:摆的 越 ,摆速越快,摆的 越 ,摆速越慢。
3、请分别在需要改变的条件和不改变的条件前打钩。
A、改变的条件:1、摆锤的轻重 2、摆绳的长短
B、不变的条件:1、摆锤的轻重 2、摆绳的长短 3、摆幅的大小
4、每次摆动的时间15秒
摆锤的轻重
摆锤
重
摆锤
轻
实验过程:
1、先用1倍的摆锤重量做三次,再用2倍的摆锤重量做三次,用3倍的摆锤重量做三次。
2、每次用时15秒。
3、认真计数,做好记录。
1.观察时间:15秒。
2.分工:
(1)一位同学记时; (2)一位同学填写实验记录单;(3)一位同学操作; (4)其余同学数摆动次数。
3.如果摆碰到了其它的物体,实验就要重来。
4.记录时把字写大一些。
实验要求
操作提示
1、用手指夹住摆锤,将摆线拉直慢慢抬高(不能过高)。检查摆线与横杆是否垂直。
2、松开手指,使摆自然摆动。摆锤摆动必须严格控制在一个竖直平面内振动。
3、计算摆球振动次数时,以摆锤通过最低位置时开始计时较准确。
4、摆来回一次经过最低点为一个周期,最后的实验数据可以取平均数或众数。
5、使用秒表时先看是否在零的位置,回表后开始计时。第二、三次应注意回表。
15秒内摆动次数记录表
摆的快慢与摆锤的重量有关系吗?
第一次 第二次 第三次
原来重量
两倍重量
三倍重量
我的发现
15秒内摆动次数记录表
摆的快慢与摆锤的重量有关系吗?
16
16
16
16
16
16
16
16
16
摆的快慢与摆锤的重量
没有关系。
第一次 第二次 第三次
原来重量
两倍重量
三倍重量
我的发现
1、我们的假设:摆的摆动快慢与 有关。
2、我们的猜测:摆的 越 ,摆速越快,摆的 越 ,摆速越慢。
3、请分别在需要改变的条件和不改变的条件前打钩。
A、改变的条件:1、摆锤的轻重 2、摆绳的长短
B、不变的条件:1、摆锤的轻重 2、摆绳的长短 3、摆幅的大小
4、每次摆动的时间15秒
摆绳的长度
摆绳
长
摆绳
短
实验过程:
1、先用1倍的摆绳长度做三次,再用2倍的摆绳长度做三次。
2、每次用时15秒。
3、认真计数,做好记录。
实验结论:
摆的快慢与摆长有关。摆长越长摆动越慢,摆长越短摆动越快。
摆的快慢与摆长长短关系的
实验报告单
摆长长短单位厘米 实验结果(15秒内摆动次数) 出现次数最多的数
第一次 第二次 第三次
1倍摆长
2倍摆长
实验结论:
摆的快慢与摆长有关。摆长越长摆动越慢,摆长越短摆动越快。
摆的快慢与摆长长短关系的
实验报告单
摆长长短单位厘米 实验结果(15秒内摆动次数) 出现次数最多的数
第一次 第二次 第三次
1倍摆长
2倍摆长
摆的快慢的实验结论:
1. 摆的快慢与摆锤的重量大小没有关系。
2.摆的快慢跟摆长有关,摆长越长摆动越慢,摆长越短摆动越快。
观察:这两个摆有什么相同的地方?有什么不同的地方?
你觉得它们摆的快慢会一样吗?
6摆的研究
伽利略的故事
1582年的一天,伽利略到教堂作礼拜.一位修理工人不经意触动了教堂中的大吊灯,使它来回摆动.伽利略观察着,脑海里闪出测量吊灯摆动时间的念头.起初,吊灯在一个大圆弧上摆动,摆动速度较大,伽利略测算来回摆动一次的时间.后来,吊灯摆动的幅度变小了,摆动速度也变慢了,他又测量了来回摆动一次的时间.他大吃一惊,两次测量的时间是相同的.伽利略继续测量,直到吊灯几乎停止摆动.伽利略发现:吊灯来回摆动一次需要的时间与摆动幅度的大小无关,无论摆幅大小如何,来回摆动一次所需时间是相同的.即吊灯的摆动具有等时性,这就是伽利略最初的发现.
伽利略发现摆的故事
伽利略发现摆的故事
他被吊灯摆动的节律性吸引住了
——— 观察
每摆动一次的时间相等吗?摆幅大些,每摆动一次的时间还相等吗?
———— 提出疑问和假设
伽利略模仿吊灯进行实验,研究摆的特点
——— 实验探究
摆的等时性原理
———— 分析得出结论
生活中的摆——摆的应用
摆长
摆锤
摆
摆角
1、我们的假设:摆的摆动快慢与 有关。
2、我们的猜测:摆的 越 ,摆速越快,摆的 越 ,摆速越慢。
3、请分别在需要改变的条件和不改变的条件前打钩。
A、改变的条件:1、摆锤的轻重 2、摆绳的长短
B、不变的条件:1、摆锤的轻重 2、摆绳的长短 3、摆幅的大小
4、每次摆动的时间15秒
摆锤的轻重
摆锤
重
摆锤
轻
实验过程:
1、先用1倍的摆锤重量做三次,再用2倍的摆锤重量做三次,用3倍的摆锤重量做三次。
2、每次用时15秒。
3、认真计数,做好记录。
1.观察时间:15秒。
2.分工:
(1)一位同学记时; (2)一位同学填写实验记录单;(3)一位同学操作; (4)其余同学数摆动次数。
3.如果摆碰到了其它的物体,实验就要重来。
4.记录时把字写大一些。
实验要求
操作提示
1、用手指夹住摆锤,将摆线拉直慢慢抬高(不能过高)。检查摆线与横杆是否垂直。
2、松开手指,使摆自然摆动。摆锤摆动必须严格控制在一个竖直平面内振动。
3、计算摆球振动次数时,以摆锤通过最低位置时开始计时较准确。
4、摆来回一次经过最低点为一个周期,最后的实验数据可以取平均数或众数。
5、使用秒表时先看是否在零的位置,回表后开始计时。第二、三次应注意回表。
15秒内摆动次数记录表
摆的快慢与摆锤的重量有关系吗?
第一次 第二次 第三次
原来重量
两倍重量
三倍重量
我的发现
15秒内摆动次数记录表
摆的快慢与摆锤的重量有关系吗?
16
16
16
16
16
16
16
16
16
摆的快慢与摆锤的重量
没有关系。
第一次 第二次 第三次
原来重量
两倍重量
三倍重量
我的发现
1、我们的假设:摆的摆动快慢与 有关。
2、我们的猜测:摆的 越 ,摆速越快,摆的 越 ,摆速越慢。
3、请分别在需要改变的条件和不改变的条件前打钩。
A、改变的条件:1、摆锤的轻重 2、摆绳的长短
B、不变的条件:1、摆锤的轻重 2、摆绳的长短 3、摆幅的大小
4、每次摆动的时间15秒
摆绳的长度
摆绳
长
摆绳
短
实验过程:
1、先用1倍的摆绳长度做三次,再用2倍的摆绳长度做三次。
2、每次用时15秒。
3、认真计数,做好记录。
实验结论:
摆的快慢与摆长有关。摆长越长摆动越慢,摆长越短摆动越快。
摆的快慢与摆长长短关系的
实验报告单
摆长长短单位厘米 实验结果(15秒内摆动次数) 出现次数最多的数
第一次 第二次 第三次
1倍摆长
2倍摆长
实验结论:
摆的快慢与摆长有关。摆长越长摆动越慢,摆长越短摆动越快。
摆的快慢与摆长长短关系的
实验报告单
摆长长短单位厘米 实验结果(15秒内摆动次数) 出现次数最多的数
第一次 第二次 第三次
1倍摆长
2倍摆长
摆的快慢的实验结论:
1. 摆的快慢与摆锤的重量大小没有关系。
2.摆的快慢跟摆长有关,摆长越长摆动越慢,摆长越短摆动越快。
观察:这两个摆有什么相同的地方?有什么不同的地方?
你觉得它们摆的快慢会一样吗?
同课章节目录
- 沉和浮
- 1、物体在水中是沉还是浮
- 2、沉浮与什么因素有关
- 3、橡皮泥在水中的沉浮
- 4、造一艘小船
- 5、浮力
- 6、下沉的物体会受到水的浮力吗
- 7、马铃薯在液体中的沉浮
- 8、探索马铃薯沉浮的原因
- 热
- 1、热起来了
- 2、给冷水加热
- 3、液体的热胀冷缩
- 4、空气的热胀冷缩
- 5、金属热胀冷缩吗
- 6、热是怎样传递的
- 7、传热比赛
- 8、设计制作一个保温杯
- 时间的测量
- 1、时间在流逝
- 2、太阳钟
- 3、用水测量时间
- 4、我的水钟
- 5、机械摆钟
- 6、摆的研究
- 7、做一个钟摆
- 8、制作一个一分钟计时器
- 地球的运动
- 1、昼夜交替现象
- 2、人类认识地球及其运动的历史
- 3、证明地球在自转
- 4、谁先迎来黎明
- 5、 北极星“不动”的秘密
- 6、地球会公转吗
- 7、为什么一年有四季
- 8、极昼和极夜的解释
