湘教版七年级数学下册课件1.2.1代入消元法(15张)
文档属性
| 名称 | 湘教版七年级数学下册课件1.2.1代入消元法(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 16:47:04 | ||
图片预览





文档简介
课件15张PPT。第一章
二元一次方程组七年级数学湘教版·下册1.2.1代入消元法教学目标1.掌握用代入法解二元一次方程的步骤;
2.会用代入法解二元一次方程组.(重点、难点)
新课导入观察与思考 问题:根据篮球比赛规则:赢一场得2分,输一场得1分.已知某次中学生篮球联赛中,某球队共赛了12场,积20分.求该球队赢了几场?输了几场?解:设该球队赢了x场,输了y场,则怎么求x,y的值呢?x+y=12
2x+y=20新知探究 昨天,我们8个人去红叶公园玩,买门票花了34元. 每张成人票5元,每张儿童票3元.他们到底去了几个成人、几个儿童呢?还记得下面这一问题吗?设他们中有x个成人,y个儿童. 我们列出的二元一次方程组为x+y=8,
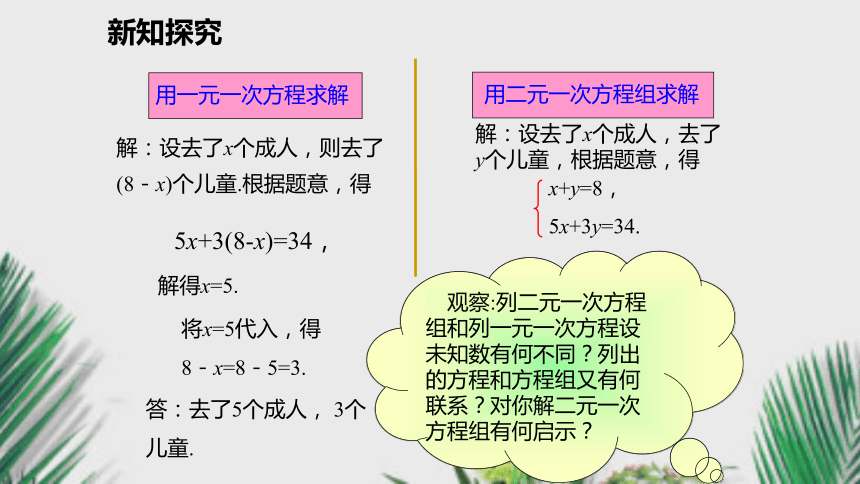
5x+3y=34.新知探究解:设去了x个成人,则去了(8-x)个儿童.根据题意,得 解得x=5.将x=5代入,得
8-x=8-5=3.答:去了5个成人, 3个儿童. 解:设去了x个成人,去了y个儿童,根据题意,得 观察:列二元一次方程组和列一元一次方程设未知数有何不同?列出的方程和方程组又有何联系?对你解二元一次方程组有何启示? 5x+3(8-x)=34,x+y=8,
5x+3y=34.新知探究由①得y = 8-x. ③将③代入②得5x+3(8-x)=34.解得x = 5.把x = 5代入③得y = 3.所以原方程组的解为x+y=8①
5x+3y=34②新知探究归纳总结 解二元一次方程组的基本思路是消元,把“二元”变为“一元”. 前面解方程组是将其中一个方程的某个未知数用含另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程.这种解方程组的方法称为代入消元法,简称代入法.新知探究典例精析例 解方程组 2x+3y=16, ① x+4y=13 . ② 新知探究归纳总结用代入法解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,
将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的另一个方程中,可得
一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代
入每一个方程看是否成立.新知探究 用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形. 本课小结解二元一次方程组基本思路“消元”代入法解二元一次方程组的一般步骤变:用含一个未知数的式子表示另一个未知数代:用这个式子替代另一个方程中相应未知数求:求出两个未知数的值写:写出方程组的解课堂小测1.方程组的解是( )B.
C. D.A.B2.二元一次方程组的解是( ) A.B.C.D.D课堂小测y=2x
x+y=12 (1)(2)2x=y-5
4x+3y=65解:(1)x=4,
y=8;(2)3.解下列方程组.x=5,
y=15.课堂小测课堂小测 4.根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g),两种产品的销售数量(按瓶计算)的比为2:5.某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶? 解:设这些消毒液应该分装x瓶大瓶、y瓶小瓶.根据题意,可列方程组:解方程组,得 答:这些消毒液应分装20000瓶大瓶,50000瓶小瓶.小技巧:当相同未知数的系数成倍数关系时,我们常用整体代入法会使解法更加快捷简便!
2.会用代入法解二元一次方程组.(重点、难点)
新课导入观察与思考 问题:根据篮球比赛规则:赢一场得2分,输一场得1分.已知某次中学生篮球联赛中,某球队共赛了12场,积20分.求该球队赢了几场?输了几场?解:设该球队赢了x场,输了y场,则怎么求x,y的值呢?x+y=12
2x+y=20新知探究 昨天,我们8个人去红叶公园玩,买门票花了34元. 每张成人票5元,每张儿童票3元.他们到底去了几个成人、几个儿童呢?还记得下面这一问题吗?设他们中有x个成人,y个儿童. 我们列出的二元一次方程组为x+y=8,
5x+3y=34.新知探究解:设去了x个成人,则去了(8-x)个儿童.根据题意,得 解得x=5.将x=5代入,得
8-x=8-5=3.答:去了5个成人, 3个儿童. 解:设去了x个成人,去了y个儿童,根据题意,得 观察:列二元一次方程组和列一元一次方程设未知数有何不同?列出的方程和方程组又有何联系?对你解二元一次方程组有何启示? 5x+3(8-x)=34,x+y=8,
5x+3y=34.新知探究由①得y = 8-x. ③将③代入②得5x+3(8-x)=34.解得x = 5.把x = 5代入③得y = 3.所以原方程组的解为x+y=8①
5x+3y=34②新知探究归纳总结 解二元一次方程组的基本思路是消元,把“二元”变为“一元”. 前面解方程组是将其中一个方程的某个未知数用含另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程.这种解方程组的方法称为代入消元法,简称代入法.新知探究典例精析例 解方程组 2x+3y=16, ① x+4y=13 . ② 新知探究归纳总结用代入法解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,
将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的另一个方程中,可得
一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代
入每一个方程看是否成立.新知探究 用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形. 本课小结解二元一次方程组基本思路“消元”代入法解二元一次方程组的一般步骤变:用含一个未知数的式子表示另一个未知数代:用这个式子替代另一个方程中相应未知数求:求出两个未知数的值写:写出方程组的解课堂小测1.方程组的解是( )B.
C. D.A.B2.二元一次方程组的解是( ) A.B.C.D.D课堂小测y=2x
x+y=12 (1)(2)2x=y-5
4x+3y=65解:(1)x=4,
y=8;(2)3.解下列方程组.x=5,
y=15.课堂小测课堂小测 4.根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g),两种产品的销售数量(按瓶计算)的比为2:5.某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶? 解:设这些消毒液应该分装x瓶大瓶、y瓶小瓶.根据题意,可列方程组:解方程组,得 答:这些消毒液应分装20000瓶大瓶,50000瓶小瓶.小技巧:当相同未知数的系数成倍数关系时,我们常用整体代入法会使解法更加快捷简便!
