六年级下册数学教案-6.2.1 图形的认识与测量(平面图形)
文档属性
| 名称 | 六年级下册数学教案-6.2.1 图形的认识与测量(平面图形) |  | |
| 格式 | zip | ||
| 文件大小 | 132.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 07:32:28 | ||
图片预览

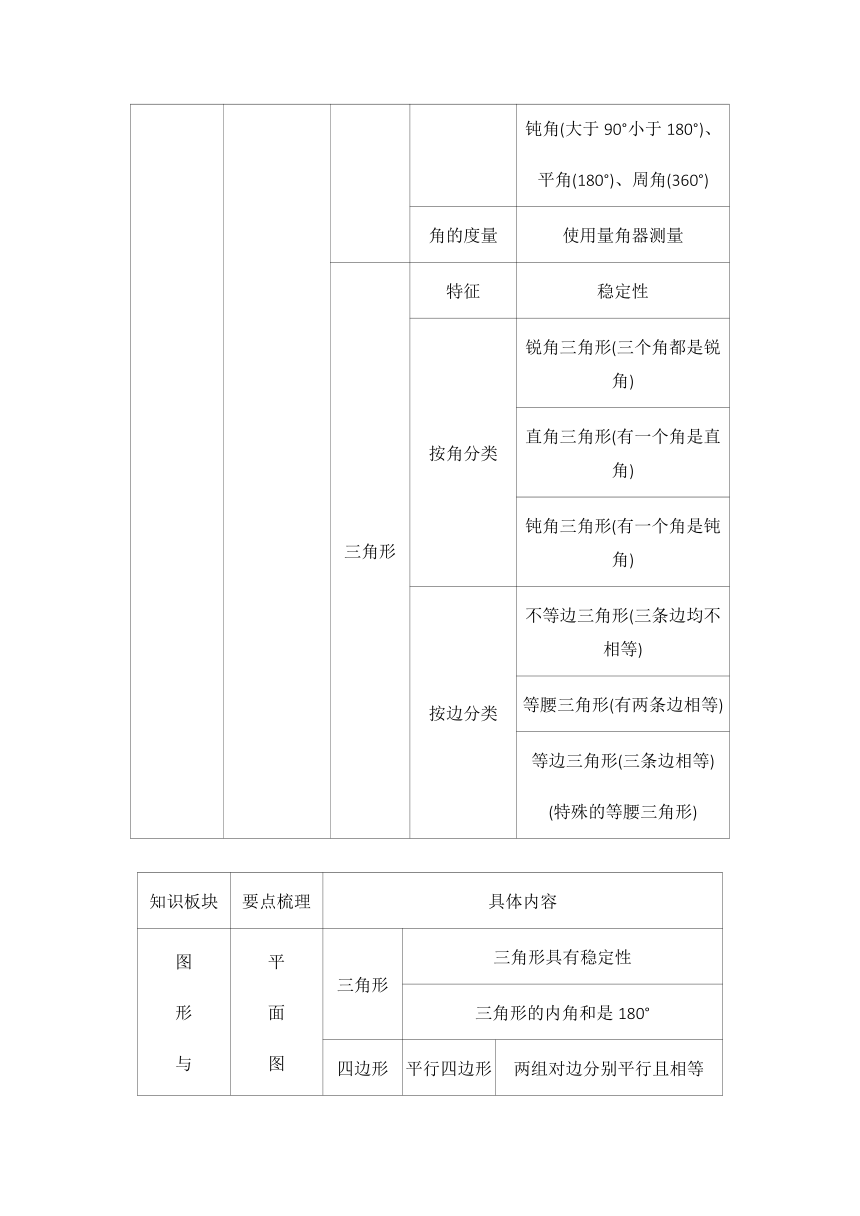



文档简介
第六单元 整理和复习
2.图形与几何
第1课时 图形的认识与测量(平面图形)
知识板块
要点梳理
具体内容
图
形
与
几
何
平
面
图
形
的
分
类
及
特
点
线
分类
直线
没有端点,无法度量
射线
一个端点,无法度量
线段
两个端点,可以度量
位置关系
(同一平面内)
相交
垂直(相交成直角)
不垂直(相交不成直角)
平行
不相交
距离
点到直线的距离
垂线段最短
平行线间的距离
都相等
角
角的意义
从一点引出两条射线所组成的图形
角的大小
与两条边张开的大小有关
角的分类
锐角(小于90°)、直角(90°)、
钝角(大于90°小于180°)、
平角(180°)、周角(360°)
角的度量
使用量角器测量
三角形
特征
稳定性
按角分类
锐角三角形(三个角都是锐角)
直角三角形(有一个角是直角)
钝角三角形(有一个角是钝角)
按边分类
不等边三角形(三条边均不相等)
等腰三角形(有两条边相等)
等边三角形(三条边相等)
(特殊的等腰三角形)
知识板块
要点梳理
具体内容
图
形
与
几
何
平
面
图
形
的
分
类
及
特
点
三角形
三角形具有稳定性
三角形的内角和是180°
四边形
平行四边形
两组对边分别平行且相等
长方形
四个角都是直角,对边平行且相等
正方形
特殊的长方形,四个角都是直角且四条边都相等
梯形
只有一组对边平行
圆
各部分名称
圆心(O)、直径(d)、半径(r)
平面图形的
周长和面积
计算公式
名称
周长(C)计算公式
面积(S)计算公式
长方形
C=2(a+b)
S=ab
正方形
C=4a
S=a2
平行四边形
——
S=ah
梯形
——
S=(a+b)h÷2
圆
C=πd或C=2πr
S=πr2
三角形
——
S=ah÷2
教材知识荟
【考点一】线
判断。
(1)不相交的两条直线叫作平行线。 ( )
(2)一条射线长5 m。 ( )
(3)过直线外一点画已知直线的平行线,可以画1条。 ( )
思路分析:(1)在同一平面内,不相交的两条直线叫作平行线。所以此题错误。
(2)射线不能度量,所以此题错误。
(3)正确。
解答:(1)× (2)× (3)√
【练习】
1.填空。
(1)过一点可以画( )条射线,过两点可以画( )条线段。
(2)直线有( )个端点,射线有( )个端点,线段有( )个端点。
(3)在同一平面内,两条直线要么( ),要么( )。
答案:(1)无数 1 (2)0 1 2 (3)平行 相交
【考点二】角
判断。
(1)一个角的两边越长,这个角就会越大。 ( )
(2)平角是一条直线,一条直线就是180°。 ( )
(3)下面各图形,哪些是角?哪些不是角?是的画“√”,不是的画“×”。
思路分析:(1)一个角的大小由角两边的张口大小决定,与角两边的长短没有关系。
(2)平角是等于180°的角,直线没有端点,是把线段向两端无限延长得到的。
(3)根据角的定义来判断,角是从一点引出两条射线所组成的图形。
解答:(1)× (2)×
(3)
填空。
(1)一个角有( )个顶点、( )条边。
(2)请你给下图的角的各部分填上名称。
思路分析:(1)根据角的定义完成此题,即从一点引出两条射线所组成的图形。
(2)根据角的组成完成此题,即角是由一个顶点和两条边组成。
解答:(1)1 2
(2)
【练习】
1.我能做好。
(1)判断下面的图形哪些是角,是角的在( )里画“√”,不是的画“×”。
(2)用三角板比比下面哪个是直角,是直角的在( )里画“√”,不是的画“×”。
(3)数一数,下面图形中各有几个角?填在( )里。
答案:(1)( √ ) ( × ) ( × ) ( × ) ( √ ) ( √ )
(2)( × ) ( √ ) ( √ ) ( × ) ( √ )
(3)( 3 ) ( 4 ) ( 6 ) ( 4 )
2.我会画。
在方格纸上画一个直角。
答案:
【考点三】三角形
填空。
(1)直角三角形除一个直角外,其余两个角一定是( )角。
(2)一个三角形,其中两个角分别是40°和60°,这个三角形是( )角三角形。
(3)三角形按角可分为( )三角形、( )三角形、( )三角形。
思路分析:(1)根据三角形的内角和是180°,一个角是直角即90°,那么其余两个角的和就是90°,说明两个角都小于90°,所以一定是锐角。
(2)根据三角形的内角和是180°,其中两个角分别是40°和60°,可求出另外一个角是80°,三个角都是锐角,可判断是锐角三角形。
(3)根据三角形的分类完成此题,即三角形按角可分为:锐角三角形、直角三角形和钝角三角形。
解答:(1)锐 (2)锐 (3)锐角 直角 钝角
【练习】
1.填空。
(1)一个三角形最多可以画( )条高。
(2)由三条( )围成的图形叫三角形。
(3)一个等腰三角形,其中一个角是50°,它的另外两个角可能是( )和( ),也可能是( )和( )。
答案:(1)3 (2)线段 (3)65° 65° 50° 80°
2.判断。
(1)等腰三角形一定是锐角三角形。 ( )
(2)一个三角形中,最大的角是锐角,那么这个三角形一定是锐角三角形。 ( )
(3)用三根分别长15厘米、24厘米和8厘米的小木棒,一定能摆出一个三角形。 ( )
答案:(1)× (2)√ (3)×
【考点四】四边形
判断。
(1)一组对边平行的四边形叫作梯形。 ( )
(2)一组对边平行的四边形叫作平行四边形。 ( )
思路分析 (1)一组对边平行,另一组对边不平行的四边形才是梯形,所以错误。
(2)两组对边分别平行且相等的四边形叫作平行四边形,所以错误。
解答 (1)× (2)×
选择。
(1)梯形的高有( )条。
A.一 B.两 C.三 D.无数
(2)在一个等腰梯形中画一条线段,可以将它分割成两个完全一样的( )。
A.梯形 B.平行四边形 C.三角形 D.正方形
(3)下列四边形中( )不是轴对称图形。
A. B. C. D.
(4)把一个长方形框架拉成一个平行四边形,这个平行四边形的周长比原长方形的周长( )。
A.大 B.小 C.一样大 D.无法比较
思路分析:(1)梯形的高:夹在两底之间的垂线段有无数条,所以选择D;
(2)画出连接上底、下底的中点的线段,即可分出两个完全一样的梯形,所以选择A;
(3)在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫作轴对称图形,以上三个图形只有A不能沿一条直线折叠后完全重合,所以选择A;
(4)周长是围成一个封闭图形的线段的长度,长方形框架拉成一个平行四边形,由于四条边的长度没有变化,所以它们的周长一样大,选择C。
解答 (1)D (2)A (3)A (4)C
【练习】
1.填一填。
(1)两组对边分别( )的四边形叫作平行四边形。
(2)常见的四边形有( )。
(3)只有一组对边平行的四边形叫作( )。
(4)( )的梯形叫作等腰梯形。
答案:(1)平行且相等 (2)平行四边形、长方形、正方形、梯形 (3)梯形 (4)两腰相等
2.大显身手。
(1)过直线外一点作已知直线的垂线和平行线。
(2)画出下面平行四边形的高。
(3)按要求在下面图形中画一条线段。
①分成两个梯形。
②分成一个三角形和一个平行四边形。
答案:
(答案不唯一)
【考点五】圆
填空。
(1)( )确定圆的大小,( )确定圆的位置。
(2)在同一个圆内,半径是直径的( ),直径是半径的( )。
(3)两个半径不等的同心圆之间的部分叫作( )。
思路分析:(1)根据圆的特点完成此题;
(2)根据圆的特征完成此题。
(3)根据圆环的定义完成此题。
解答:(1)半径 圆心 (2)一半 二倍 (3)圆环
【练习】
1.填写表格。
半径(r)
3厘米
1.8分米
10厘米
直径(d)
4厘米
0.7米
答案:从左向右为:6厘米 2厘米 3.6分米 0.35米 20厘米
2.画一个直径4厘米的圆,标出圆心、半径和直径。
答案:略
【考点六】 平面图形的周长与面积计算公式
下图中,边长为10 cm和15 cm的两个正方形并放在一起,求三角形ABC(阴影部分)的面积。
思路分析:三角形ADC的面积是10×15÷2=75(cm2),如果三角形ABC和三角形BCD都以BC边为底,又已知三角形ABC的高是三角形BCD高的(15÷10=1.5)倍,那么三角形ABC的面积是三角形BCD的1.5倍。阴影部分面积是75÷(1+1.5)×1.5=45(cm2)。
解答:10×15÷2=75(cm2) 75÷(1+1.5)×1.5=45(cm2)
填表。
图形
已知条件
周长/m
面积/m2
长方形
a=8,b=6
正方形
a=7
平行四边形
a=10,h=8
/
三角形
a=15,h=10
/
梯形
a=12,b=18,h=8
/
圆
r=2
思路分析:根据平面图形的周长和面积公式完成此题。
解答:
图形
已知条件
周长/m
面积/m2
长方形
a=8,b=6
28
48
正方形
a=7
28
49
平行四边形
a=10,h=8
/
80
三角形
a=15,h=10
/
75
梯形
a=12,b=18,h=8
/
120
圆
r=2
12.56
12.56
【练习】
1.填空。
(1)一个时钟的时针长5 cm,一昼夜时针针尖走了( )cm。
(2)一个圆的半径扩大到原来的2倍,周长扩大到原来的( ),面积扩大到原来的( )。
(3)用一根长2米的绳子将一只羊拴在一根木桩上,这只羊最多能吃到( )平方米的草。
答案:(1)62.8 (2)2倍 4倍 (3)12.56
2.选择。
(1)用一根铁丝围成正方形、长方形和圆,面积最大的是( )。
A.长方形 B.正方形 C.圆
(2)一个平行四边形和一个三角形等底等高,已知平行四边形的面积是50 cm2,那么三角形的面积是( )cm2。
A.30 B.50 C.25
答案:(1)C (2)C
3.解决问题。
(1)一个梯形广告牌,它的上底是6 m,下底是10 m,高是8 m。如果要给这个广告牌涂上油漆,按每平方米花费15元来计算,共要花多少元?
(2)王奶奶家用65 m长的竹篱笆在一块靠墙的空地上围了一个菜园(如图),这个菜园的面积是多少平方米?
(3)在一个半径4 m的圆形花坛周围修一条宽2 m的甬道,甬道的面积是多少平方米?
(4)一块三角形菜地的面积是0.25公顷,菜地的底是50 m,高是多少米?
解答:(1)(6+10)×8÷2×15=960(元)
(2)(65-20)×20÷2=450(m2)
(3)3.14×[(4+2)2-42]=62.8(m2)
(4)0.25公顷=2500 m2 2500×2÷50=100(m)
我的反思:
?
?
?
?
?
?
?
2.图形与几何
第1课时 图形的认识与测量(平面图形)
知识板块
要点梳理
具体内容
图
形
与
几
何
平
面
图
形
的
分
类
及
特
点
线
分类
直线
没有端点,无法度量
射线
一个端点,无法度量
线段
两个端点,可以度量
位置关系
(同一平面内)
相交
垂直(相交成直角)
不垂直(相交不成直角)
平行
不相交
距离
点到直线的距离
垂线段最短
平行线间的距离
都相等
角
角的意义
从一点引出两条射线所组成的图形
角的大小
与两条边张开的大小有关
角的分类
锐角(小于90°)、直角(90°)、
钝角(大于90°小于180°)、
平角(180°)、周角(360°)
角的度量
使用量角器测量
三角形
特征
稳定性
按角分类
锐角三角形(三个角都是锐角)
直角三角形(有一个角是直角)
钝角三角形(有一个角是钝角)
按边分类
不等边三角形(三条边均不相等)
等腰三角形(有两条边相等)
等边三角形(三条边相等)
(特殊的等腰三角形)
知识板块
要点梳理
具体内容
图
形
与
几
何
平
面
图
形
的
分
类
及
特
点
三角形
三角形具有稳定性
三角形的内角和是180°
四边形
平行四边形
两组对边分别平行且相等
长方形
四个角都是直角,对边平行且相等
正方形
特殊的长方形,四个角都是直角且四条边都相等
梯形
只有一组对边平行
圆
各部分名称
圆心(O)、直径(d)、半径(r)
平面图形的
周长和面积
计算公式
名称
周长(C)计算公式
面积(S)计算公式
长方形
C=2(a+b)
S=ab
正方形
C=4a
S=a2
平行四边形
——
S=ah
梯形
——
S=(a+b)h÷2
圆
C=πd或C=2πr
S=πr2
三角形
——
S=ah÷2
教材知识荟
【考点一】线
判断。
(1)不相交的两条直线叫作平行线。 ( )
(2)一条射线长5 m。 ( )
(3)过直线外一点画已知直线的平行线,可以画1条。 ( )
思路分析:(1)在同一平面内,不相交的两条直线叫作平行线。所以此题错误。
(2)射线不能度量,所以此题错误。
(3)正确。
解答:(1)× (2)× (3)√
【练习】
1.填空。
(1)过一点可以画( )条射线,过两点可以画( )条线段。
(2)直线有( )个端点,射线有( )个端点,线段有( )个端点。
(3)在同一平面内,两条直线要么( ),要么( )。
答案:(1)无数 1 (2)0 1 2 (3)平行 相交
【考点二】角
判断。
(1)一个角的两边越长,这个角就会越大。 ( )
(2)平角是一条直线,一条直线就是180°。 ( )
(3)下面各图形,哪些是角?哪些不是角?是的画“√”,不是的画“×”。
思路分析:(1)一个角的大小由角两边的张口大小决定,与角两边的长短没有关系。
(2)平角是等于180°的角,直线没有端点,是把线段向两端无限延长得到的。
(3)根据角的定义来判断,角是从一点引出两条射线所组成的图形。
解答:(1)× (2)×
(3)
填空。
(1)一个角有( )个顶点、( )条边。
(2)请你给下图的角的各部分填上名称。
思路分析:(1)根据角的定义完成此题,即从一点引出两条射线所组成的图形。
(2)根据角的组成完成此题,即角是由一个顶点和两条边组成。
解答:(1)1 2
(2)
【练习】
1.我能做好。
(1)判断下面的图形哪些是角,是角的在( )里画“√”,不是的画“×”。
(2)用三角板比比下面哪个是直角,是直角的在( )里画“√”,不是的画“×”。
(3)数一数,下面图形中各有几个角?填在( )里。
答案:(1)( √ ) ( × ) ( × ) ( × ) ( √ ) ( √ )
(2)( × ) ( √ ) ( √ ) ( × ) ( √ )
(3)( 3 ) ( 4 ) ( 6 ) ( 4 )
2.我会画。
在方格纸上画一个直角。
答案:
【考点三】三角形
填空。
(1)直角三角形除一个直角外,其余两个角一定是( )角。
(2)一个三角形,其中两个角分别是40°和60°,这个三角形是( )角三角形。
(3)三角形按角可分为( )三角形、( )三角形、( )三角形。
思路分析:(1)根据三角形的内角和是180°,一个角是直角即90°,那么其余两个角的和就是90°,说明两个角都小于90°,所以一定是锐角。
(2)根据三角形的内角和是180°,其中两个角分别是40°和60°,可求出另外一个角是80°,三个角都是锐角,可判断是锐角三角形。
(3)根据三角形的分类完成此题,即三角形按角可分为:锐角三角形、直角三角形和钝角三角形。
解答:(1)锐 (2)锐 (3)锐角 直角 钝角
【练习】
1.填空。
(1)一个三角形最多可以画( )条高。
(2)由三条( )围成的图形叫三角形。
(3)一个等腰三角形,其中一个角是50°,它的另外两个角可能是( )和( ),也可能是( )和( )。
答案:(1)3 (2)线段 (3)65° 65° 50° 80°
2.判断。
(1)等腰三角形一定是锐角三角形。 ( )
(2)一个三角形中,最大的角是锐角,那么这个三角形一定是锐角三角形。 ( )
(3)用三根分别长15厘米、24厘米和8厘米的小木棒,一定能摆出一个三角形。 ( )
答案:(1)× (2)√ (3)×
【考点四】四边形
判断。
(1)一组对边平行的四边形叫作梯形。 ( )
(2)一组对边平行的四边形叫作平行四边形。 ( )
思路分析 (1)一组对边平行,另一组对边不平行的四边形才是梯形,所以错误。
(2)两组对边分别平行且相等的四边形叫作平行四边形,所以错误。
解答 (1)× (2)×
选择。
(1)梯形的高有( )条。
A.一 B.两 C.三 D.无数
(2)在一个等腰梯形中画一条线段,可以将它分割成两个完全一样的( )。
A.梯形 B.平行四边形 C.三角形 D.正方形
(3)下列四边形中( )不是轴对称图形。
A. B. C. D.
(4)把一个长方形框架拉成一个平行四边形,这个平行四边形的周长比原长方形的周长( )。
A.大 B.小 C.一样大 D.无法比较
思路分析:(1)梯形的高:夹在两底之间的垂线段有无数条,所以选择D;
(2)画出连接上底、下底的中点的线段,即可分出两个完全一样的梯形,所以选择A;
(3)在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫作轴对称图形,以上三个图形只有A不能沿一条直线折叠后完全重合,所以选择A;
(4)周长是围成一个封闭图形的线段的长度,长方形框架拉成一个平行四边形,由于四条边的长度没有变化,所以它们的周长一样大,选择C。
解答 (1)D (2)A (3)A (4)C
【练习】
1.填一填。
(1)两组对边分别( )的四边形叫作平行四边形。
(2)常见的四边形有( )。
(3)只有一组对边平行的四边形叫作( )。
(4)( )的梯形叫作等腰梯形。
答案:(1)平行且相等 (2)平行四边形、长方形、正方形、梯形 (3)梯形 (4)两腰相等
2.大显身手。
(1)过直线外一点作已知直线的垂线和平行线。
(2)画出下面平行四边形的高。
(3)按要求在下面图形中画一条线段。
①分成两个梯形。
②分成一个三角形和一个平行四边形。
答案:
(答案不唯一)
【考点五】圆
填空。
(1)( )确定圆的大小,( )确定圆的位置。
(2)在同一个圆内,半径是直径的( ),直径是半径的( )。
(3)两个半径不等的同心圆之间的部分叫作( )。
思路分析:(1)根据圆的特点完成此题;
(2)根据圆的特征完成此题。
(3)根据圆环的定义完成此题。
解答:(1)半径 圆心 (2)一半 二倍 (3)圆环
【练习】
1.填写表格。
半径(r)
3厘米
1.8分米
10厘米
直径(d)
4厘米
0.7米
答案:从左向右为:6厘米 2厘米 3.6分米 0.35米 20厘米
2.画一个直径4厘米的圆,标出圆心、半径和直径。
答案:略
【考点六】 平面图形的周长与面积计算公式
下图中,边长为10 cm和15 cm的两个正方形并放在一起,求三角形ABC(阴影部分)的面积。
思路分析:三角形ADC的面积是10×15÷2=75(cm2),如果三角形ABC和三角形BCD都以BC边为底,又已知三角形ABC的高是三角形BCD高的(15÷10=1.5)倍,那么三角形ABC的面积是三角形BCD的1.5倍。阴影部分面积是75÷(1+1.5)×1.5=45(cm2)。
解答:10×15÷2=75(cm2) 75÷(1+1.5)×1.5=45(cm2)
填表。
图形
已知条件
周长/m
面积/m2
长方形
a=8,b=6
正方形
a=7
平行四边形
a=10,h=8
/
三角形
a=15,h=10
/
梯形
a=12,b=18,h=8
/
圆
r=2
思路分析:根据平面图形的周长和面积公式完成此题。
解答:
图形
已知条件
周长/m
面积/m2
长方形
a=8,b=6
28
48
正方形
a=7
28
49
平行四边形
a=10,h=8
/
80
三角形
a=15,h=10
/
75
梯形
a=12,b=18,h=8
/
120
圆
r=2
12.56
12.56
【练习】
1.填空。
(1)一个时钟的时针长5 cm,一昼夜时针针尖走了( )cm。
(2)一个圆的半径扩大到原来的2倍,周长扩大到原来的( ),面积扩大到原来的( )。
(3)用一根长2米的绳子将一只羊拴在一根木桩上,这只羊最多能吃到( )平方米的草。
答案:(1)62.8 (2)2倍 4倍 (3)12.56
2.选择。
(1)用一根铁丝围成正方形、长方形和圆,面积最大的是( )。
A.长方形 B.正方形 C.圆
(2)一个平行四边形和一个三角形等底等高,已知平行四边形的面积是50 cm2,那么三角形的面积是( )cm2。
A.30 B.50 C.25
答案:(1)C (2)C
3.解决问题。
(1)一个梯形广告牌,它的上底是6 m,下底是10 m,高是8 m。如果要给这个广告牌涂上油漆,按每平方米花费15元来计算,共要花多少元?
(2)王奶奶家用65 m长的竹篱笆在一块靠墙的空地上围了一个菜园(如图),这个菜园的面积是多少平方米?
(3)在一个半径4 m的圆形花坛周围修一条宽2 m的甬道,甬道的面积是多少平方米?
(4)一块三角形菜地的面积是0.25公顷,菜地的底是50 m,高是多少米?
解答:(1)(6+10)×8÷2×15=960(元)
(2)(65-20)×20÷2=450(m2)
(3)3.14×[(4+2)2-42]=62.8(m2)
(4)0.25公顷=2500 m2 2500×2÷50=100(m)
我的反思:
?
?
?
?
?
?
?
