六年级下册数学教案图形的认识与测量(立体图形)表格式
文档属性
| 名称 | 六年级下册数学教案图形的认识与测量(立体图形)表格式 |
|
|
| 格式 | zip | ||
| 文件大小 | 63.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 00:00:00 | ||
图片预览


文档简介
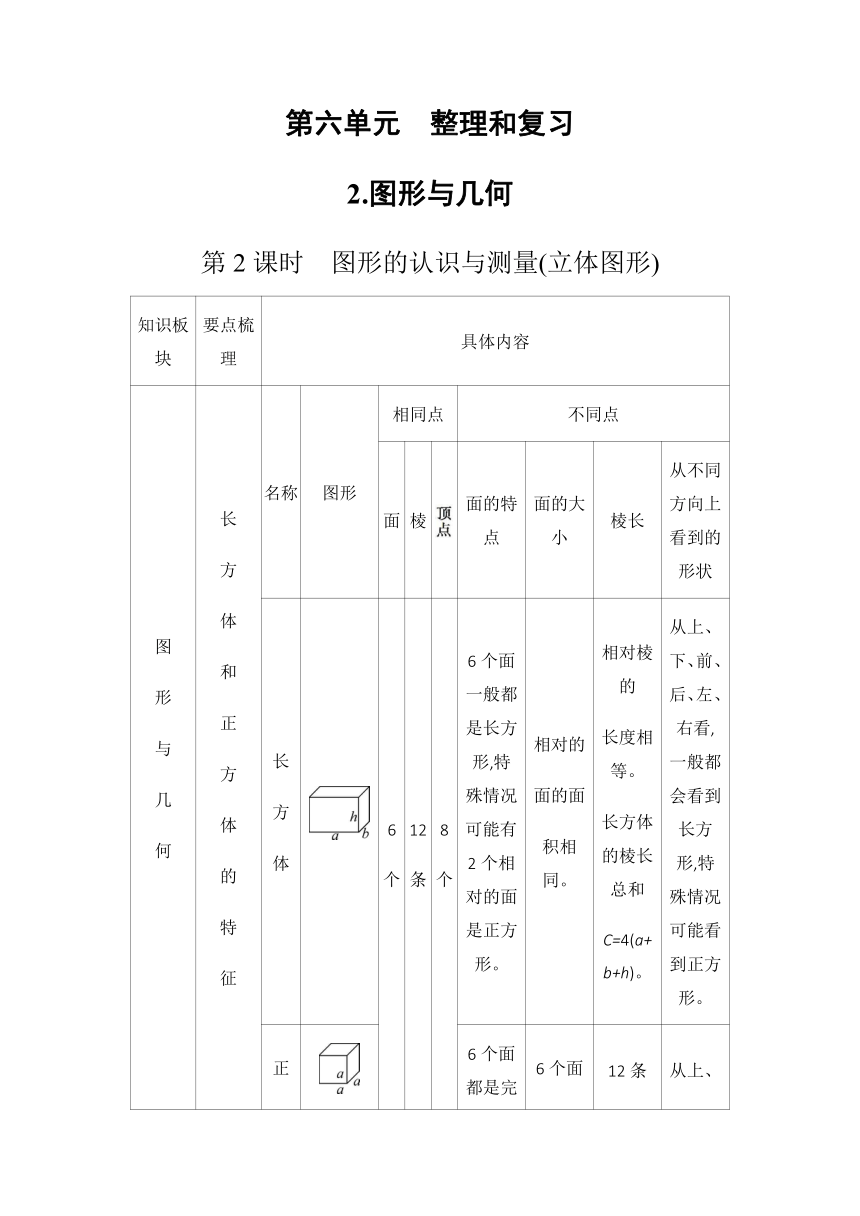
第六单元 整理和复习
2.图形与几何
第2课时 图形的认识与测量(立体图形)
知识板块
要点梳理
具体内容
图
形
与
几
何
长
方
体
和
正
方
体
的
特
征
名称
图形
相同点
不同点
面
棱
面的特点
面的大小
棱长
从不同方向上看到的形状
长
方
体
6
个
12
条
8
个
6个面一般都是长方形,特殊情况可能有2个相对的面是正方形。
相对的
面的面
积相同。
相对棱的
长度相等。
长方体的棱长总和
C=4(a+b+h)。
从上、下、前、后、左、右看,一般都会看到长方形,特殊情况可能看到正方形。
正
方
体
6个面都是完全相同的正方
形。
6个面
的面积
都相等。
12条棱
的长度都相等。正方体的棱长总和:C=12a。
从上、下、
前、后、左、
右看,都会看到一
个正方形。
圆
柱
与
圆
锥
的
特
征
名称
图形
特征
从不同方向上看到的形状
圆
柱
1.圆柱有3个面,上、下两个底面是大小相同的圆,侧面是曲面。
2.圆柱两底面之间的距离叫作高,它有无数条高。
3.圆柱沿侧面上的高展开后是长方形(或正方形)。
4.以长方形或正方形的一条边为轴旋转一周形成圆柱。
1.从上或下看,会看到一个圆。
2.从侧面看,会看到一个长方形(或正方形)。
知识板块
要点梳理
具体内容
空
间
与
几
何
圆
柱
与
圆
锥
的
特
征
名称
图形
特征
从不同方向上看到的形状
圆
锥
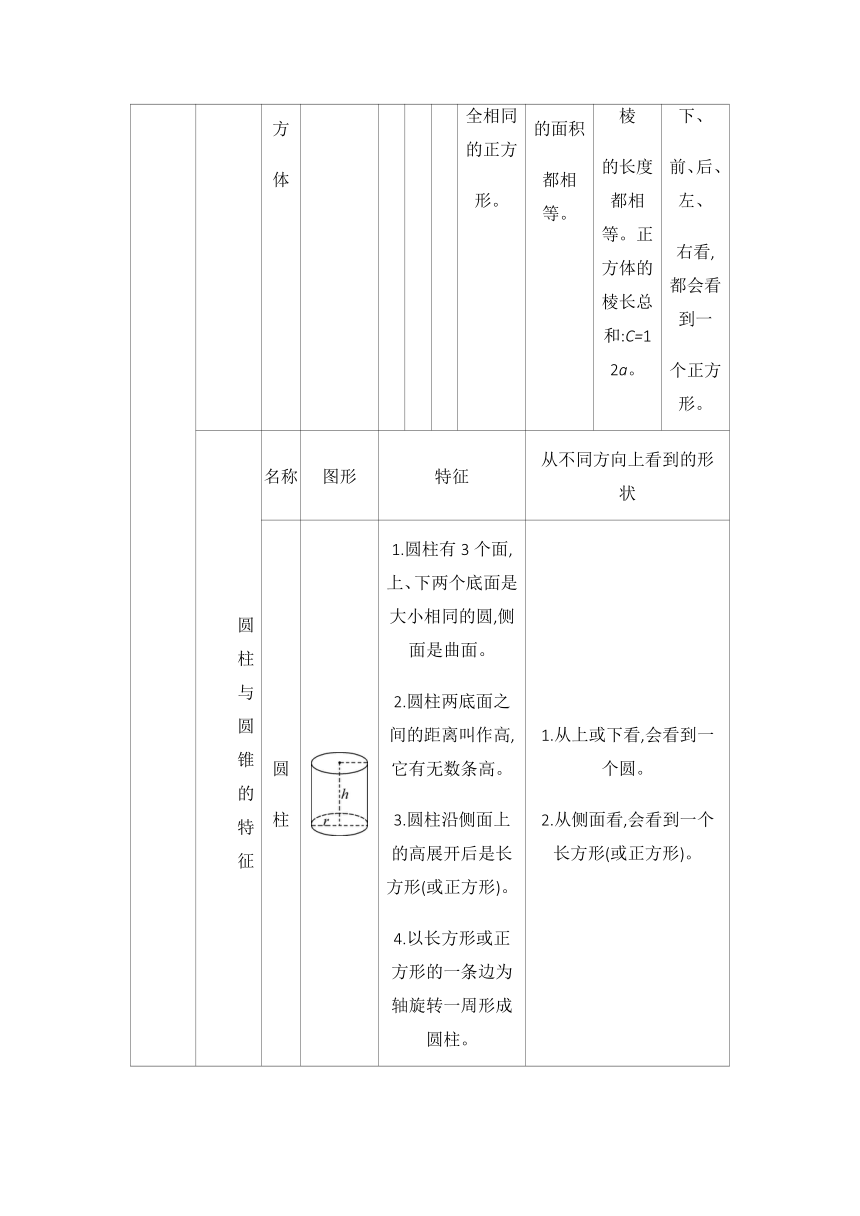
1.圆锥有2个面,它的底面是圆,侧面是曲面。
2.圆锥的顶点到底面圆心的距离叫作高,圆锥只有一条高。
3.以直角三角形的一条直角边为轴旋转一周形成圆锥。
1.从上面看,会看到☉。
2.从下面看,会看到一个圆。
3.从侧面看,会看到一个等腰三角形。
立
体
图
形
的
表
面
积
和
体
积
1.表面积:一个立体图形所有面的面积总和。
2.体积:一个立体图形所占空间的大小。
名称
图形
字母意义
侧面积
表面积
体积
长
方
体
a—长
b—宽
h—高
S=
2(a+b)h
S=
(ab+ah
+bh)×2
V=abh
V=Sh
正
方
体
a—棱长
S=4a2
S=6a2
V=a3
圆
柱
r—底面半径h—高
C—底面周长
S=Ch
=2πrh
S=2πrh
+2πr2
V=πr2h
圆
锥
S—底面积
r—底面半径
h—高
——
——
V=Sh=πr2h
教材知识荟
【考点一】 长方体和正方体的特征
判断。
(1)圆柱的侧面展开一定是正方形。 ( )
(2)以直角三角形的一条直角边为轴旋转一周形成的图形是圆锥。 ( )
(3)把一根长24 cm的铁丝制作成一个正方体框架,棱长是3 cm。 ( )
思路分析 (1)圆柱的特征:沿侧面上的高展开后是长方形(或正方形),所以此题错误。
(2)以直角三角形的一条直角边为轴旋转一周形成圆锥,所以此题正确。
(3)正方体有12条长度相等的棱,24÷12=2(厘米),此题错误。
解答:(1)× (2)√ (3)×
【练习】
填空。
(1)正方体有( )条棱、( )个顶点,每个面都是( )形,正方体是特殊的( )。
(2)长方体至少有( )个面是长方形。
答案:(1)12 8 正方 长方体
(2)4
【考点二】圆柱和圆锥的特征
填空。
(1)圆柱的两个底面都是( )。
(2)圆柱的侧面是一个( )面,把它沿着高展开可能是一个( )形或( )形。
(3)圆锥的高有( )条,圆柱的高有( )条。
思路分析:(1)根据圆柱的构成完成此题,圆柱有3个面,上、下2个底面是大小相同的圆,侧面是曲面。
(2)根据圆柱的特征完成此题,圆柱沿侧面上的高展开后是长方形(或正方形)。
(3)根据圆柱、圆锥的特征完成此题,圆柱两底面之间的距离叫作高,它有无数条高;圆锥的顶点到底面圆心的距离叫作高,圆锥只有一条高。
答案:(1)圆 (2)曲 长方 正方 (3)1 无数
【练习】
1.判断。
(1)如果一个长方体有两个面是正方形,那么其他4个面的面积相等。 ( )
(2)圆柱的侧面沿高展开是一个长方形或正方形。 ( )
(3)长方体的三条棱就是它的长、宽、高。 ( )
答案:(1)√ (2)√ (3)×
2.填空。
(1)长方体和正方体都有( )个面、( )个顶点、( )条棱,长方体两个相对的面( ),相对的棱( ),正方体六个面都是( ),所有的棱( )。
(2)圆柱的侧面沿着一条( )展开会得到一个( ),它的长等于圆柱的( ),它的宽等于圆柱的( )。
(3)以一个长6厘米、宽4厘米的长方形的宽为轴旋转一周会得到一个( ),它的底面半径是( )厘米,高是( )厘米。
(4)以直角三角形的一条( )为轴,旋转一周得到的图形是( ),另有一条直角边是( )。
答案:(1)6 8 12 完全相同 长度相等 正方形 长度相等
(2)高 长方形或正方形 底面周长 高
(3)圆柱 6 4
(4)直角边 圆锥 底面半径
【考点三】 立体图形的表面积和体积
一个圆柱的侧面展开图是正方形,已知它的底面周长是31.4 cm,它的体积是多少?
思路分析:当底面周长与高相等时,圆柱的侧面展开图是正方形,所以底面周长是31.4 cm,说明圆柱的高也是31.4 cm。根据底面周长求出底面半径,进而求出底面面积,最后求得体积。
解答:31.4÷3.14÷2=5 (cm) 3.14×52×31.4=2464.9 (cm2)
求下列立体图形的底面周长和底面积。
思路分析:根据圆的面积和周长计算公式计算圆柱和圆锥的底面周长和底面积。
解答:圆柱:底面周长 3.14×3×2=18.84(cm)
底面积 3.14×32=28.26(cm2)
圆锥:底面周长 3.14×10=31.4(m)
底面积 3.14×(10÷2)2=78.5(m2)
【练习】
(1)做一个圆柱形油桶,底面直径是0.6 m,高是1 m,至少需要多少平方米铁皮?(得数保留整数)
(2)一个圆柱的底面直径是6 cm,高是10 cm,体积是多少?
(3)一个圆锥的底面半径是5 m,高是6 m,体积是多少?
答案:(1) 底面积:3.14×(0.6÷2)2=0.2826(m2)
侧面积:3.14×0.6×1=1.884(m2)
表面积:0.2826×2+1.884=2.4492(m2)≈3(m2)
(2)底面积:3.14×(6÷2)2=28.26(m2)
体积: 28.26×10=282.6(m3)
(3)×3.14×52×6=157(m3)
我的反思:
?
?
?
?
?
?
?
?
?
?
?
?
?
2.图形与几何
第2课时 图形的认识与测量(立体图形)
知识板块
要点梳理
具体内容
图
形
与
几
何
长
方
体
和
正
方
体
的
特
征
名称
图形
相同点
不同点
面
棱
面的特点
面的大小
棱长
从不同方向上看到的形状
长
方
体
6
个
12
条
8
个
6个面一般都是长方形,特殊情况可能有2个相对的面是正方形。
相对的
面的面
积相同。
相对棱的
长度相等。
长方体的棱长总和
C=4(a+b+h)。
从上、下、前、后、左、右看,一般都会看到长方形,特殊情况可能看到正方形。
正
方
体
6个面都是完全相同的正方
形。
6个面
的面积
都相等。
12条棱
的长度都相等。正方体的棱长总和:C=12a。
从上、下、
前、后、左、
右看,都会看到一
个正方形。
圆
柱
与
圆
锥
的
特
征
名称
图形
特征
从不同方向上看到的形状
圆
柱
1.圆柱有3个面,上、下两个底面是大小相同的圆,侧面是曲面。
2.圆柱两底面之间的距离叫作高,它有无数条高。
3.圆柱沿侧面上的高展开后是长方形(或正方形)。
4.以长方形或正方形的一条边为轴旋转一周形成圆柱。
1.从上或下看,会看到一个圆。
2.从侧面看,会看到一个长方形(或正方形)。
知识板块
要点梳理
具体内容
空
间
与
几
何
圆
柱
与
圆
锥
的
特
征
名称
图形
特征
从不同方向上看到的形状
圆
锥
1.圆锥有2个面,它的底面是圆,侧面是曲面。
2.圆锥的顶点到底面圆心的距离叫作高,圆锥只有一条高。
3.以直角三角形的一条直角边为轴旋转一周形成圆锥。
1.从上面看,会看到☉。
2.从下面看,会看到一个圆。
3.从侧面看,会看到一个等腰三角形。
立
体
图
形
的
表
面
积
和
体
积
1.表面积:一个立体图形所有面的面积总和。
2.体积:一个立体图形所占空间的大小。
名称
图形
字母意义
侧面积
表面积
体积
长
方
体
a—长
b—宽
h—高
S=
2(a+b)h
S=
(ab+ah
+bh)×2
V=abh
V=Sh
正
方
体
a—棱长
S=4a2
S=6a2
V=a3
圆
柱
r—底面半径h—高
C—底面周长
S=Ch
=2πrh
S=2πrh
+2πr2
V=πr2h
圆
锥
S—底面积
r—底面半径
h—高
——
——
V=Sh=πr2h
教材知识荟
【考点一】 长方体和正方体的特征
判断。
(1)圆柱的侧面展开一定是正方形。 ( )
(2)以直角三角形的一条直角边为轴旋转一周形成的图形是圆锥。 ( )
(3)把一根长24 cm的铁丝制作成一个正方体框架,棱长是3 cm。 ( )
思路分析 (1)圆柱的特征:沿侧面上的高展开后是长方形(或正方形),所以此题错误。
(2)以直角三角形的一条直角边为轴旋转一周形成圆锥,所以此题正确。
(3)正方体有12条长度相等的棱,24÷12=2(厘米),此题错误。
解答:(1)× (2)√ (3)×
【练习】
填空。
(1)正方体有( )条棱、( )个顶点,每个面都是( )形,正方体是特殊的( )。
(2)长方体至少有( )个面是长方形。
答案:(1)12 8 正方 长方体
(2)4
【考点二】圆柱和圆锥的特征
填空。
(1)圆柱的两个底面都是( )。
(2)圆柱的侧面是一个( )面,把它沿着高展开可能是一个( )形或( )形。
(3)圆锥的高有( )条,圆柱的高有( )条。
思路分析:(1)根据圆柱的构成完成此题,圆柱有3个面,上、下2个底面是大小相同的圆,侧面是曲面。
(2)根据圆柱的特征完成此题,圆柱沿侧面上的高展开后是长方形(或正方形)。
(3)根据圆柱、圆锥的特征完成此题,圆柱两底面之间的距离叫作高,它有无数条高;圆锥的顶点到底面圆心的距离叫作高,圆锥只有一条高。
答案:(1)圆 (2)曲 长方 正方 (3)1 无数
【练习】
1.判断。
(1)如果一个长方体有两个面是正方形,那么其他4个面的面积相等。 ( )
(2)圆柱的侧面沿高展开是一个长方形或正方形。 ( )
(3)长方体的三条棱就是它的长、宽、高。 ( )
答案:(1)√ (2)√ (3)×
2.填空。
(1)长方体和正方体都有( )个面、( )个顶点、( )条棱,长方体两个相对的面( ),相对的棱( ),正方体六个面都是( ),所有的棱( )。
(2)圆柱的侧面沿着一条( )展开会得到一个( ),它的长等于圆柱的( ),它的宽等于圆柱的( )。
(3)以一个长6厘米、宽4厘米的长方形的宽为轴旋转一周会得到一个( ),它的底面半径是( )厘米,高是( )厘米。
(4)以直角三角形的一条( )为轴,旋转一周得到的图形是( ),另有一条直角边是( )。
答案:(1)6 8 12 完全相同 长度相等 正方形 长度相等
(2)高 长方形或正方形 底面周长 高
(3)圆柱 6 4
(4)直角边 圆锥 底面半径
【考点三】 立体图形的表面积和体积
一个圆柱的侧面展开图是正方形,已知它的底面周长是31.4 cm,它的体积是多少?
思路分析:当底面周长与高相等时,圆柱的侧面展开图是正方形,所以底面周长是31.4 cm,说明圆柱的高也是31.4 cm。根据底面周长求出底面半径,进而求出底面面积,最后求得体积。
解答:31.4÷3.14÷2=5 (cm) 3.14×52×31.4=2464.9 (cm2)
求下列立体图形的底面周长和底面积。
思路分析:根据圆的面积和周长计算公式计算圆柱和圆锥的底面周长和底面积。
解答:圆柱:底面周长 3.14×3×2=18.84(cm)
底面积 3.14×32=28.26(cm2)
圆锥:底面周长 3.14×10=31.4(m)
底面积 3.14×(10÷2)2=78.5(m2)
【练习】
(1)做一个圆柱形油桶,底面直径是0.6 m,高是1 m,至少需要多少平方米铁皮?(得数保留整数)
(2)一个圆柱的底面直径是6 cm,高是10 cm,体积是多少?
(3)一个圆锥的底面半径是5 m,高是6 m,体积是多少?
答案:(1) 底面积:3.14×(0.6÷2)2=0.2826(m2)
侧面积:3.14×0.6×1=1.884(m2)
表面积:0.2826×2+1.884=2.4492(m2)≈3(m2)
(2)底面积:3.14×(6÷2)2=28.26(m2)
体积: 28.26×10=282.6(m3)
(3)×3.14×52×6=157(m3)
我的反思:
?
?
?
?
?
?
?
?
?
?
?
?
?
