湘教版七年级数学下册课件2.1.2.2积的乘方(16张)
文档属性
| 名称 | 湘教版七年级数学下册课件2.1.2.2积的乘方(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览






文档简介
课件16张PPT。第二章
整式的乘法七年级数学湘教版·下册2.1.2.2积的乘方教学目标1.理解并掌握积的乘方法则及其应用.(重点)
2.会运用积的乘方的运算法则进行计算.(难点)新课导入 1.计算:
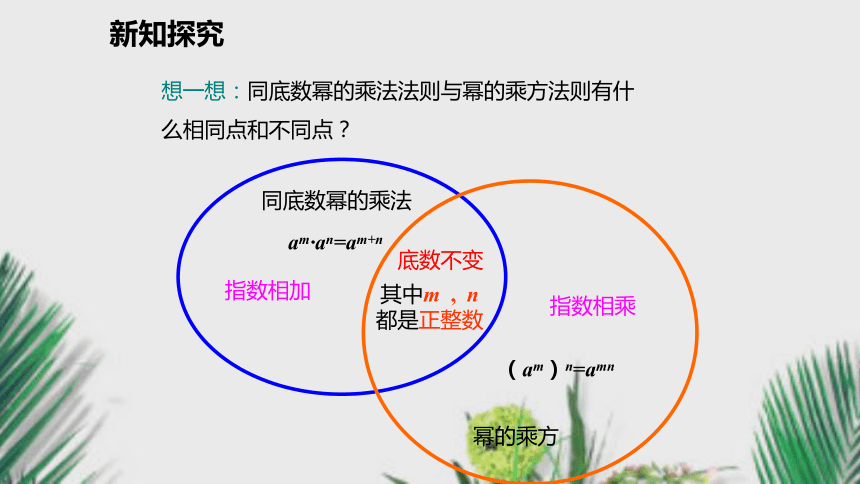
(1) 10×102× 103 =______ ;(2) (x5 )2=_________.x101062.(1)同底数幂的乘法 :am·an= ( m,n都是正整数).am+n (2)幂的乘方:(am)n= (m,n都是正整数).amn回顾与思考新知探究底数不变指数相乘指数相加其中m , n都是正整数(am)n=amnam·an=am+n想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?新知探究思考下面两道题:(1)(2)我们可以根据乘方的意义及乘法交换律、结合律进行运算.这两道题有什么特点?底数为两个因式相乘,积的形式.这种形式为积的乘方我们学过的幂的乘方的运算性质适用吗?自主探究新知探究同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)新知探究=anbn.证明:思考问题:积的乘方(ab)n =?猜想结论: 因此可得:(ab)n=anbn (n为正整数). (ab)n=anbn (n为正整数) 推理验证新知探究 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘. (ab)n = anbn (n为正整数) 想一想:三个或三个以上的积的乘方等于什么? (abc)n = anbncn (n为正整数)积的乘方法则新知探究例1 计算:
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4. 解:(1)原式= (2)原式= (3)原式= (4)原式== 8a3.=-125b3. =x2y4.=16x12.23a3(-5)3b3x2(y2)2(-2)4(x3)4括号内每一个因式都要乘方.新知探究解:原式逆用幂的乘方的运算性质幂的乘方的运算性质逆用同底数幂的乘法运算性质逆用积的乘方的运算性质例2 计算: 新知探究an·bn = (ab)n am+n =am·anamn =(am)n作用:使运算更加简便快捷!本课小结幂的运算性质性质 am·an=am+n (am)n=amn
(ab)n=anbn ( m,n都是正整数)反向运用
am · an =am+n
(am)n =amn
an·bn = (ab)n
可使某些计算简捷注意运用积的乘方法则时要注意:
公式中的a,b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)课堂小测(1)(ab2)3=ab6 ( ) ×××(2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( )(4) -(-ab2)2=a2b4 ( )1.判断: 2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4C课堂小测 (1) (ab)8 ; (2) (2m)3 ; (3) (-xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (-3×103)3.3.计算: 解:(1)原式=a8·b8.(2)原式= 23 ·m3=8m3.(3)原式=(-x)5 ·y5=-x5y5.(4)原式=53 ·a3 ·(b2)3=125 a3 b6.(5)原式=22 ×(102)2=4 ×104.(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
课堂小测(1)2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2. 解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9
= 0.解:原式=9x2y4 +4x2y4 =13x2y4.解:原式= -8x9·x4 =-8x13. 注意:运算顺序是
先乘方,再乘除,
最后算加减.4.计算:结果中如果有同类项的要合并.课堂小测5.如果(an?bm?b)3=a9b15,求m, n的值.? (an)3?(bm)3?b3=a9b15,? a 3n ?b 3m?b3=a9b15 ,? a 3n ?b 3m+3=a9b15,? 3n=9 ,3m+3=15.?n=3,m=4.解: ∵(an?bm?b)3=a9b15,
2.会运用积的乘方的运算法则进行计算.(难点)新课导入 1.计算:
(1) 10×102× 103 =______ ;(2) (x5 )2=_________.x101062.(1)同底数幂的乘法 :am·an= ( m,n都是正整数).am+n (2)幂的乘方:(am)n= (m,n都是正整数).amn回顾与思考新知探究底数不变指数相乘指数相加其中m , n都是正整数(am)n=amnam·an=am+n想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?新知探究思考下面两道题:(1)(2)我们可以根据乘方的意义及乘法交换律、结合律进行运算.这两道题有什么特点?底数为两个因式相乘,积的形式.这种形式为积的乘方我们学过的幂的乘方的运算性质适用吗?自主探究新知探究同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)新知探究=anbn.证明:思考问题:积的乘方(ab)n =?猜想结论: 因此可得:(ab)n=anbn (n为正整数). (ab)n=anbn (n为正整数) 推理验证新知探究 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘. (ab)n = anbn (n为正整数) 想一想:三个或三个以上的积的乘方等于什么? (abc)n = anbncn (n为正整数)积的乘方法则新知探究例1 计算:
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4. 解:(1)原式= (2)原式= (3)原式= (4)原式== 8a3.=-125b3. =x2y4.=16x12.23a3(-5)3b3x2(y2)2(-2)4(x3)4括号内每一个因式都要乘方.新知探究解:原式逆用幂的乘方的运算性质幂的乘方的运算性质逆用同底数幂的乘法运算性质逆用积的乘方的运算性质例2 计算: 新知探究an·bn = (ab)n am+n =am·anamn =(am)n作用:使运算更加简便快捷!本课小结幂的运算性质性质 am·an=am+n (am)n=amn
(ab)n=anbn ( m,n都是正整数)反向运用
am · an =am+n
(am)n =amn
an·bn = (ab)n
可使某些计算简捷注意运用积的乘方法则时要注意:
公式中的a,b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)课堂小测(1)(ab2)3=ab6 ( ) ×××(2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( )(4) -(-ab2)2=a2b4 ( )1.判断: 2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4C课堂小测 (1) (ab)8 ; (2) (2m)3 ; (3) (-xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (-3×103)3.3.计算: 解:(1)原式=a8·b8.(2)原式= 23 ·m3=8m3.(3)原式=(-x)5 ·y5=-x5y5.(4)原式=53 ·a3 ·(b2)3=125 a3 b6.(5)原式=22 ×(102)2=4 ×104.(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
课堂小测(1)2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2. 解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9
= 0.解:原式=9x2y4 +4x2y4 =13x2y4.解:原式= -8x9·x4 =-8x13. 注意:运算顺序是
先乘方,再乘除,
最后算加减.4.计算:结果中如果有同类项的要合并.课堂小测5.如果(an?bm?b)3=a9b15,求m, n的值.? (an)3?(bm)3?b3=a9b15,? a 3n ?b 3m?b3=a9b15 ,? a 3n ?b 3m+3=a9b15,? 3n=9 ,3m+3=15.?n=3,m=4.解: ∵(an?bm?b)3=a9b15,
