湘教版七年级数学下册课件2.1.4.2多项式与多项式相乘(17张)
文档属性
| 名称 | 湘教版七年级数学下册课件2.1.4.2多项式与多项式相乘(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览






文档简介
课件17张PPT。第二章
整式的乘法七年级数学湘教版·下册2.1.4.2多项式与多项式相乘教学目标1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.(难点)新课导入复习引入1.如何进行单项式与多项式乘法的运算?② 再把所得的积相加.① 将单项式分别乘以多项式的各项;2.进行单项式与多项式乘法运算时,要注意什么?① 不能漏乘:即单项式要乘遍多项式的每一项;② 去括号时注意符号的确定.新知探究问题1 (a+b)X= ?
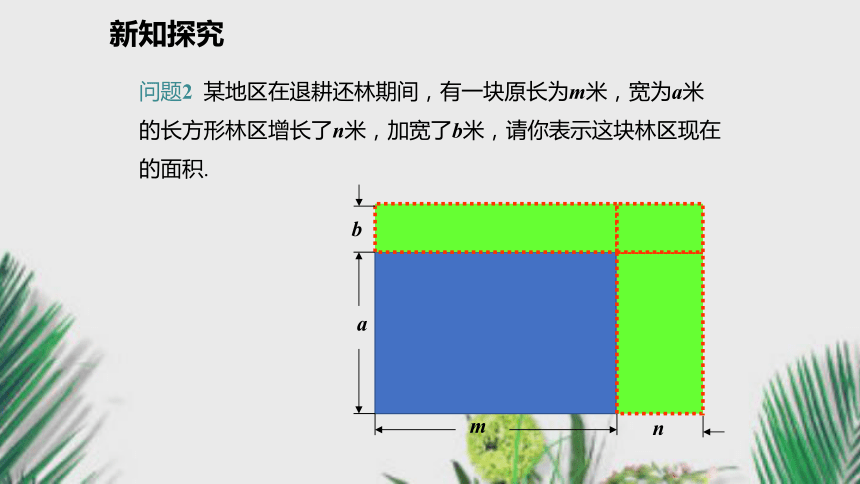
(a+b)X=aX+bX(a+b)X=(a+b)(m+n)当X=m+n时, (a+b)X=?问题引导新知探究问题2 某地区在退耕还林期间,有一块原长为m米,宽为a米的长方形林区增长了n米,加宽了b米,请你表示这块林区现在的面积.新知探究manambnb你能用不同的形式表示所拼图的面积吗?这块林区现在长为(m+n)米,宽为(a+b)米.新知探究由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb.如何进行多项式与多项式相乘的运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb.(m+n)(a+b)= (m+n)a+(m+n)b 新知探究 多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.多项式乘以多项式(a+b)(m+n)=am1234+an+bm+bn多乘多顺口溜:多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.新知探究例 计算:(1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).解: (1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y; (3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.本课小结多项式×多项式运算法则多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn注意不要漏乘;正确确定各项符号;结果要最简实质上是转化为单项式×多项式的运算(x-1)2在一般情况下不等于x2-12.课堂小测1.判别下列解法是否正确,若错请说出理由.(1)(2x-3)(x-2)-(x-1)2课堂小测(2)(2x-3)(x-2)-(x-1)2课堂小测 2.计算:(1)(x?3y)(x+7y); (2)(2x + 5y)(3x?2y).=x2 +4xy-21y2. (2) (2x +5 y)(3x?2y)==x2+7xy-3yx-21y2
2x?3x ?2x? 2y +5 y? 3x5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.?课堂小测3.计算求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.解:原式=当x=1,y=-2时,
原式=22×12-7×1×(-2)-14×(-2)2=22+14 -56
=-20.课堂小测4.小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,问小东应在挂历画上裁下一块多大面积的长方形?课堂小测面积:(2m+2b+c)(2m+a)课堂小测解:(2m+2b+c)(2m+a)= 4m2+2ma+4bm+2ab+2cm+ca.答:小东应在挂历画上裁下一块 (4m2+2ma+4bm+2ab+2cm+ca)
平方厘米的长方形.
2.能够用多项式与多项式的乘法运算法则进行计算.(难点)新课导入复习引入1.如何进行单项式与多项式乘法的运算?② 再把所得的积相加.① 将单项式分别乘以多项式的各项;2.进行单项式与多项式乘法运算时,要注意什么?① 不能漏乘:即单项式要乘遍多项式的每一项;② 去括号时注意符号的确定.新知探究问题1 (a+b)X= ?
(a+b)X=aX+bX(a+b)X=(a+b)(m+n)当X=m+n时, (a+b)X=?问题引导新知探究问题2 某地区在退耕还林期间,有一块原长为m米,宽为a米的长方形林区增长了n米,加宽了b米,请你表示这块林区现在的面积.新知探究manambnb你能用不同的形式表示所拼图的面积吗?这块林区现在长为(m+n)米,宽为(a+b)米.新知探究由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb.如何进行多项式与多项式相乘的运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb.(m+n)(a+b)= (m+n)a+(m+n)b 新知探究 多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.多项式乘以多项式(a+b)(m+n)=am1234+an+bm+bn多乘多顺口溜:多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.新知探究例 计算:(1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).解: (1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y; (3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.本课小结多项式×多项式运算法则多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn注意不要漏乘;正确确定各项符号;结果要最简实质上是转化为单项式×多项式的运算(x-1)2在一般情况下不等于x2-12.课堂小测1.判别下列解法是否正确,若错请说出理由.(1)(2x-3)(x-2)-(x-1)2课堂小测(2)(2x-3)(x-2)-(x-1)2课堂小测 2.计算:(1)(x?3y)(x+7y); (2)(2x + 5y)(3x?2y).=x2 +4xy-21y2. (2) (2x +5 y)(3x?2y)==x2+7xy-3yx-21y2
2x?3x ?2x? 2y +5 y? 3x5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.?课堂小测3.计算求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.解:原式=当x=1,y=-2时,
原式=22×12-7×1×(-2)-14×(-2)2=22+14 -56
=-20.课堂小测4.小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,问小东应在挂历画上裁下一块多大面积的长方形?课堂小测面积:(2m+2b+c)(2m+a)课堂小测解:(2m+2b+c)(2m+a)= 4m2+2ma+4bm+2ab+2cm+ca.答:小东应在挂历画上裁下一块 (4m2+2ma+4bm+2ab+2cm+ca)
平方厘米的长方形.
