苏科版八年级上册数学同步拓展1.3探索全等三角形条件学案:截长补短法(无答案)
文档属性
| 名称 | 苏科版八年级上册数学同步拓展1.3探索全等三角形条件学案:截长补短法(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 117.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 21:02:38 | ||
图片预览

文档简介
苏科版八年级上册全等三角形辅助线2-截长补短
知识导图
适用题型:经常用于证明两条线段长之和等于第三条线段的长,即a+b=c。
也适合于证明线段的和、差、倍、分之类的题目
方法要点:在最长线段上截取一条线段与较短线段中的一条相等,或是将某条较短线段延长一定长度,延长长度与另一
条较短线段相等,再利用三角形全等的有关性质加以说明.
截长法:在最长线段上截取一段与较短线段中的一条相等,再证明剩下的线段相等。
(简言之将最长线段“一分为二”)
补短法:将较短线段延长一定长度,延长长度与另一条较短线段相等,证明线段相等。
(简言之将较短线段“合二为一”)
导学一 :与角平分线有关的截长补短法
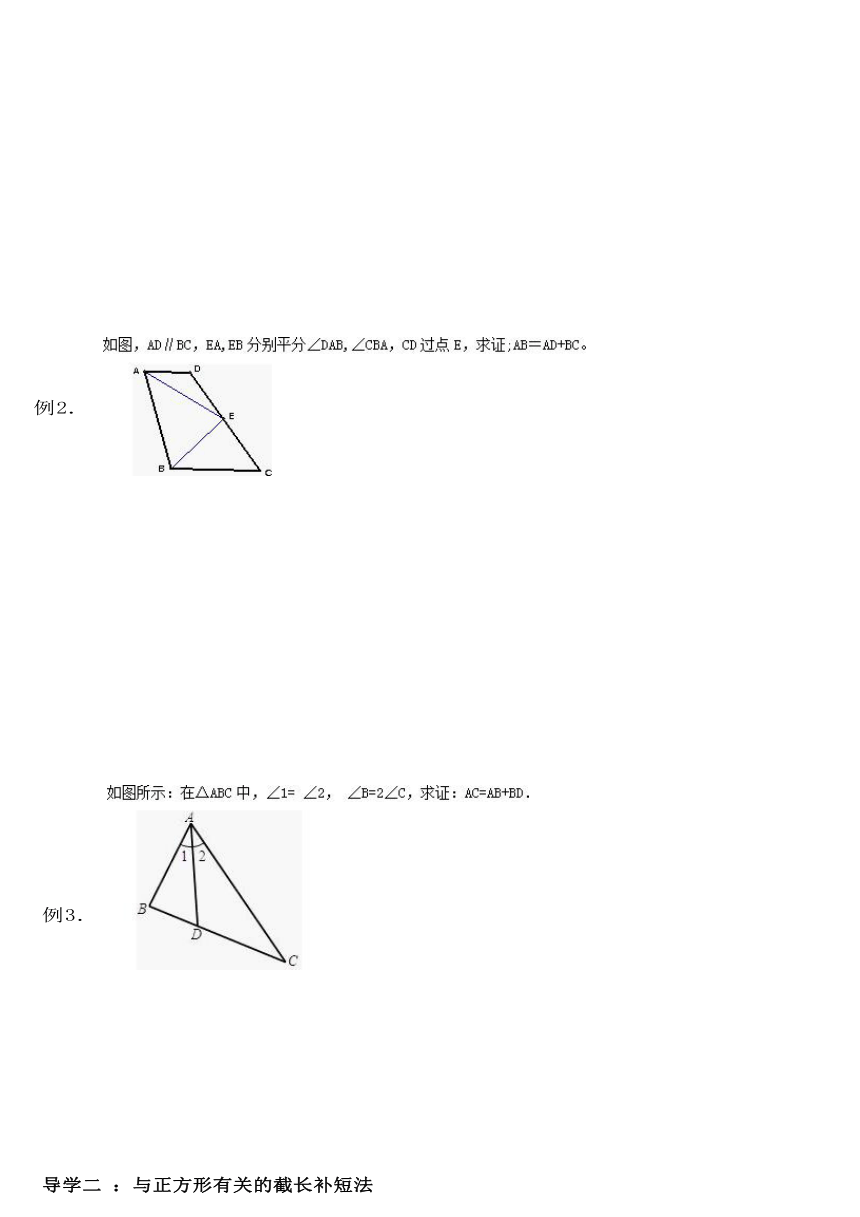
例1.
例2.
例3.
导学二 :与正方形有关的截长补短法
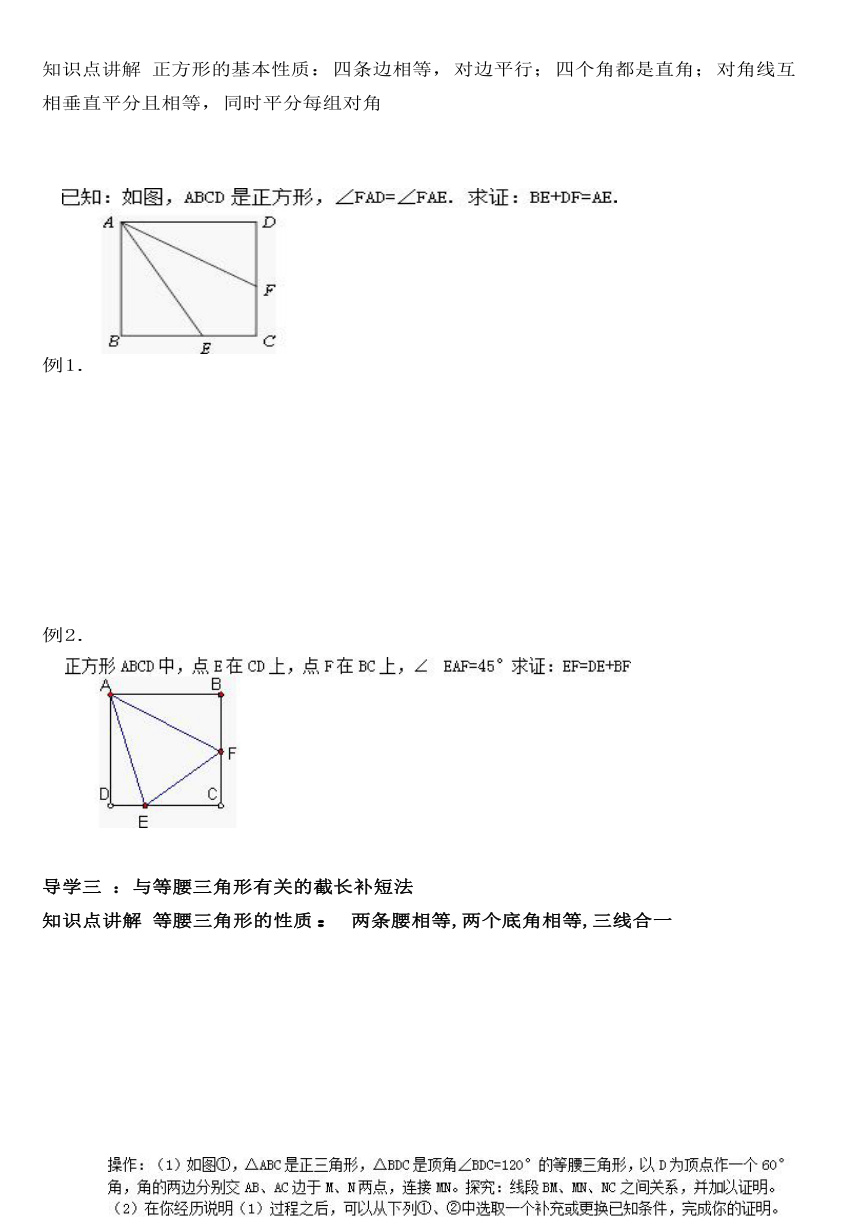
知识点讲解 正方形的基本性质:四条边相等,对边平行;四个角都是直角;对角线互相垂直平分且相等,同时平分每组对角
例1.
例2.
导学三 :与等腰三角形有关的截长补短法
知识点讲解 等腰三角形的性质:两条腰相等,两个底角相等,三线合一
例 1.
(
同步巩固
)
1.
2.
3.
4.
5、已知,如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC。求证:∠BAD+∠BCD=180°
B C
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
