人教版八年级数学 下册 第二十章 数据的分析 小结与复习 课件(共39张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 第二十章 数据的分析 小结与复习 课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-01 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
千教万教教人求真,千学万学学做真人。
——陶行知
20 数据的分析小结与复习
人教版八年级数学 下册
目标导航
1.复习基础知识,构建知识体系。
2. 典型习题探索,形成技能技巧。
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平
均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平
均数 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
基础知识
最多
中间位置的数
两个数据的平均数
中位数
定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错
提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众
数
定义 一组数据中出现次数________的数据叫做这组数据的众数
防错
提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
基础知识
1.已知数据5,5,6,x,7,7,8的平均数是6,则这组数据的中位数是( )
A.7
B.6
C.5.5
D.5
2.在航天知识竞赛中,包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为________分.
B
71
即学即练
3.由小到大的一组数:1,2,x,5,6,7中,这组数的中位数是4,则X为( )
A.2
B.3
C.4
D.5
4.数据“1,2,1,3,1”的众数是( )
A.1
B.1.5
D.3
C.1.6
B
A
即学即练
二、数据的波动程度
平均数
大
表示波
动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越___,反之也成立
基础知识
1.衡量一组数据波动大小的统计量是( )
A.平均数 B.众数 C.中位数D.方差
2.样本甲的方差是 ,样本乙的数据为2.20,2.30,2.20,2.10,2.20,则样本甲和样本乙波动大小为( )
A.甲、乙波动大小一样
B.乙波动比甲波动大
D.甲、乙波动大小无法比较
C.甲波动比乙波动大
D
C
即学即练
三、用样本估计总体
1.统计的基本思想:用样本的特征(平均数和方差)估计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多角度地去分析已有数据,从数据的变化中发现它们的规律和变化趋势,减少人为因素的影响.
基础知识
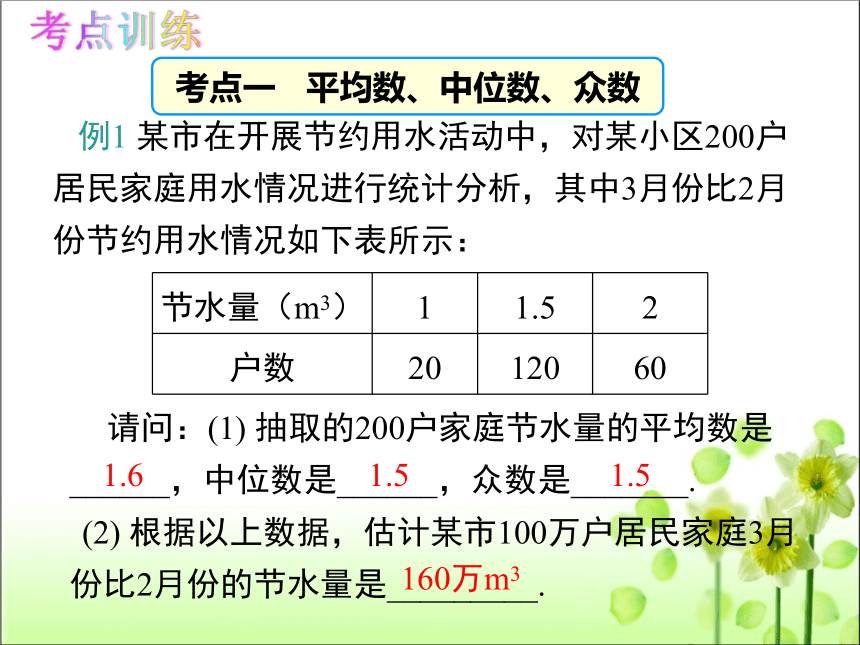
考点一 平均数、中位数、众数
例1 某市在开展节约用水活动中,对某小区200户居民家庭用水情况进行统计分析,其中3月份比2月份节约用水情况如下表所示:
节水量(m3) 1 1.5 2
户数 20 120 60
请问:(1) 抽取的200户家庭节水量的平均数是______,中位数是______,众数是_______.
(2) 根据以上数据,估计某市100万户居民家庭3月份比2月份的节水量是_________.
1.6
1.5
160万m3
1.5
考点训练
1.某米店经营某种品牌的大米,该店记录了一周中不同包装(10 kg,20 kg,50 kg)的大米的销售量(单位:袋)如下:10 kg装100袋;20 kg装220袋;
50 kg装80袋.如果每500 g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的( )
A.平均数 B.中位数 C.众数 D.最大值
C
A
2.一组数据中的一个数大小发生了变化,一定会
影响这组数据的平均数、众数、中位数中的( )
A.1个 B.2个 C.3个 D.0个
即学即练
3.某地发生地震灾害后,某中学八(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10
B.10,20
C.16,15
D.15,16
B
即学即练
4. 小刚在“中国梦·我的梦”演讲比赛中,演讲内容、语言表达、演讲技能、形象礼仪四项得分依次为9.8,9.4,9.2,9.3. 若其综合得分按演讲内容50%、语言表达20%、演讲技能20%、形象礼仪10%的比例计算,则他的综合得分是_________.
9.55
即学即练
考点二 方差的计算及应用
例2 小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题:
(1) 根据图中信息,补全下面的表格.
次数 1 2 3 4 5
小明 13.3 13.3 13.2 13.3
小亮 13.2 13.4 13.1 13.3
13.4
13.5
考点训练
解:
甲的方差:
乙的平均数:
(1)甲的平均数:
(65+80+80++85+90)÷5=80
(70+90+85+75+80)÷5=80
乙的方差:
(2)因为 ,所以乙的成绩较稳定,应该派乙去。
小张和小李去练习射击,第一轮10发子弹打完后,两人的成绩如图.根据图中的信息,小张小李两人中成绩较稳定的是 .
小张
即学即练
例3 我市某中学七、八年级各选派10名选手参加学校举办的“爱我祖国”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
考点三 分析数据做决策
考点训练
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
考点训练
(1)解:依题意,得
解得
(2)m=6,n=20%.
(3)①八年级队平均分高于七年级队;
②八年级队的成绩比七年级队稳定;
③八年级队的成绩集中在中上游,所以支持八年级队成绩好(注:任说两条即可).
(3×1+6a+7×1+8×1+9×1+10b)÷10=6.7
1+a+1+1+1+b=10
a=5,
b=1.
考点训练
经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A,B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20个,记录它们的质量如下(单位:kg):
A:4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B:4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9
5.4 5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.
即学即练
(1)若质量为(5±0.25)kg的为优等品,根据以上信息
完成下表:
解:(2)从优等品数量的角度看,因A种技术种植的西瓜优等品数量较多,所以A种技术较好;从平均数的角度看,因A种技术种植的西瓜质量的平均数更接近5kg,所以A种技术较好;
从方差的角度看,因B种技术种植的西瓜质量的方差更小,所以B种技术种植的西瓜质量更为稳定;
从市场销售角度看,因优等品更畅销,A种技术种植的西瓜优等品数量更多,且平均质量更接近5kg,因而更适合推广A种技术.
即学即练
(2)请分别从优等品数量、平均数与方差三方面对A,B两种技术做出评价;从市场销售的角度看,你认为推广哪种种植技术较好?
数据收集—数据整理—数据描述—数据分析
数据的
集中趋势
数据的
波动程度
方差
用样本平均数
估计总体平均数
用样本方差
估计总体方差
平均数
中位数
众 数
用样本估计总体
课堂小结
1.已知数据x1,x2,…,xn的平均数是2,则一组新数据x1+8,x2+8,…,xn+8的平均数是_______.
2.七(1)班四个绿化小组植树的棵树如下:10,10,x,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是______棵.
3.数据2,3,x,4的平均数是3,则这组数据的众数是________.
10
11
3
强化训练
4.对甲、乙两台机床生产的零件进行抽样测量,其平均数都是10,机床甲的方差0.02,机床乙的方差0.06,由此可知:_____(填“甲”或“乙”)机床性能较好
甲
强化训练
5.某制鞋厂准备生产一批男皮鞋,随机选出120名中年男子进行调查,得知所需鞋号的中位数是24 cm,众数是25 cm,平均数是24 cm,则下列说法正确的是( )
A.所需27 cm的鞋的人数太少,所以可以不生产
B.因为平均数为24,故这批男鞋只生产24 cm的鞋
C.因为中位数是24,故24 cm的鞋的生产量应占首位
D.因为众数是25,故25 cm的鞋的生产量要占首位
D
强化训练
6.为了从甲、乙两名学生中选拔一人参加全市初中数学联赛,对他们进行了5次测验,成绩如下:
甲:65 80 80 85 90
乙:70 90 85 75 80
(1)分别求出甲、乙两名学生5次测验成绩的平均数及方差;
(2)如果你是他们的辅导老师,应派哪名学生参加这次数学联赛?说明理由.
强化训练
(2) 分别计算成绩的平均数 和方差,填入表格. 若你是
老师,将小明与小亮的成绩
比较析后, 将分别给予他们
怎样的建议?
平均数 方差
小明
小亮
13.3
13.3
0.02
0.004
强化训练
解:从平均数看,两人的平均水平相同;从方差看,小明的成绩较稳定,小亮的成绩波动较大.
给小明的建议是:加强锻炼,提高爆发力,提升短跑成绩;
给小亮的建议是:总结经验,找出成绩忽高忽低的原因,在稳定中提高.
平均数 方差
小明
小亮
13.3
13.3
0.02
0.004
强化训练
7.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如图所示的统计图,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为____,图①中m的值为____;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
40
15
解:(2)这组样本数据的众数为35号,中位数为36号
(3)200×30%=60(双)
强化训练
8.A,B农场养奶牛200头,为了了解两奶牛场一天牛奶的产量,各随意抽取5头奶牛,称得它们的牛奶产量(单位:千克)如下:
A农场:6.3,6.9,6.5,7.9,7.4;
B农场:6.8,7.3,7.5,6.6,6.8.
(1)分别计算5头奶牛牛奶产量的平均数,估计A,B两农场中200头奶牛一天的牛奶产量;
(2)如果学校要实行“学生奶工程”,你认为选择哪个农场作为学校的长期供货方较好?
强化训练
解:(1)A农场5头奶牛牛奶产量的平均数为7千克,估计A农场200头奶牛一天的牛奶产量为7×200=1400(千克).B农场5头奶牛牛奶产量的平均数为7千克,估计B农场200头奶牛一天的牛奶产量为7×200=1400(千克) (2)A农场5头奶牛牛奶产量的方差为0.344,B农场5头奶牛牛奶产量的方差为0.116,因为0.344> 0.116,所以B农场奶牛的产量相对稳定,因此选择B农场作为供货方
强化训练
9.甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图①、图②所示的统计图
(1)在图②中画出折线表示乙队在集训期间内这五场比赛成绩的变化情况;
(2)已知甲队五场比赛成绩的平均分x甲=90分,请你计算乙队五场比赛成绩的平均分x乙;
(3)就这五场比赛,分别计算两队成绩的方差;
(4)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和方差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
强化训练
解:(1)图略 (2)x乙=90分 (3)甲队成绩的方差是41.2,乙队成绩的方差是111.6 (4)从平均分看,两队的平均分相同,实力大体相当;从折线的趋势看,甲队比赛成绩呈上升趋势,而乙队比赛成绩呈下降趋势;从获胜场数看,甲队胜三场,乙队胜两场,甲队成绩较好;从方差看,甲队比赛成绩比乙队比赛成绩波动小,甲队成绩较稳定.综上所述,选派甲队参赛更能取得好成绩
强化训练
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
千教万教教人求真,千学万学学做真人。
——陶行知
20 数据的分析小结与复习
人教版八年级数学 下册
目标导航
1.复习基础知识,构建知识体系。
2. 典型习题探索,形成技能技巧。
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平
均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平
均数 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
基础知识
最多
中间位置的数
两个数据的平均数
中位数
定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错
提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众
数
定义 一组数据中出现次数________的数据叫做这组数据的众数
防错
提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
基础知识
1.已知数据5,5,6,x,7,7,8的平均数是6,则这组数据的中位数是( )
A.7
B.6
C.5.5
D.5
2.在航天知识竞赛中,包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为________分.
B
71
即学即练
3.由小到大的一组数:1,2,x,5,6,7中,这组数的中位数是4,则X为( )
A.2
B.3
C.4
D.5
4.数据“1,2,1,3,1”的众数是( )
A.1
B.1.5
D.3
C.1.6
B
A
即学即练
二、数据的波动程度
平均数
大
表示波
动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越___,反之也成立
基础知识
1.衡量一组数据波动大小的统计量是( )
A.平均数 B.众数 C.中位数D.方差
2.样本甲的方差是 ,样本乙的数据为2.20,2.30,2.20,2.10,2.20,则样本甲和样本乙波动大小为( )
A.甲、乙波动大小一样
B.乙波动比甲波动大
D.甲、乙波动大小无法比较
C.甲波动比乙波动大
D
C
即学即练
三、用样本估计总体
1.统计的基本思想:用样本的特征(平均数和方差)估计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多角度地去分析已有数据,从数据的变化中发现它们的规律和变化趋势,减少人为因素的影响.
基础知识
考点一 平均数、中位数、众数
例1 某市在开展节约用水活动中,对某小区200户居民家庭用水情况进行统计分析,其中3月份比2月份节约用水情况如下表所示:
节水量(m3) 1 1.5 2
户数 20 120 60
请问:(1) 抽取的200户家庭节水量的平均数是______,中位数是______,众数是_______.
(2) 根据以上数据,估计某市100万户居民家庭3月份比2月份的节水量是_________.
1.6
1.5
160万m3
1.5
考点训练
1.某米店经营某种品牌的大米,该店记录了一周中不同包装(10 kg,20 kg,50 kg)的大米的销售量(单位:袋)如下:10 kg装100袋;20 kg装220袋;
50 kg装80袋.如果每500 g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的( )
A.平均数 B.中位数 C.众数 D.最大值
C
A
2.一组数据中的一个数大小发生了变化,一定会
影响这组数据的平均数、众数、中位数中的( )
A.1个 B.2个 C.3个 D.0个
即学即练
3.某地发生地震灾害后,某中学八(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10
B.10,20
C.16,15
D.15,16
B
即学即练
4. 小刚在“中国梦·我的梦”演讲比赛中,演讲内容、语言表达、演讲技能、形象礼仪四项得分依次为9.8,9.4,9.2,9.3. 若其综合得分按演讲内容50%、语言表达20%、演讲技能20%、形象礼仪10%的比例计算,则他的综合得分是_________.
9.55
即学即练
考点二 方差的计算及应用
例2 小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题:
(1) 根据图中信息,补全下面的表格.
次数 1 2 3 4 5
小明 13.3 13.3 13.2 13.3
小亮 13.2 13.4 13.1 13.3
13.4
13.5
考点训练
解:
甲的方差:
乙的平均数:
(1)甲的平均数:
(65+80+80++85+90)÷5=80
(70+90+85+75+80)÷5=80
乙的方差:
(2)因为 ,所以乙的成绩较稳定,应该派乙去。
小张和小李去练习射击,第一轮10发子弹打完后,两人的成绩如图.根据图中的信息,小张小李两人中成绩较稳定的是 .
小张
即学即练
例3 我市某中学七、八年级各选派10名选手参加学校举办的“爱我祖国”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
考点三 分析数据做决策
考点训练
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
考点训练
(1)解:依题意,得
解得
(2)m=6,n=20%.
(3)①八年级队平均分高于七年级队;
②八年级队的成绩比七年级队稳定;
③八年级队的成绩集中在中上游,所以支持八年级队成绩好(注:任说两条即可).
(3×1+6a+7×1+8×1+9×1+10b)÷10=6.7
1+a+1+1+1+b=10
a=5,
b=1.
考点训练
经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A,B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20个,记录它们的质量如下(单位:kg):
A:4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B:4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9
5.4 5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.
即学即练
(1)若质量为(5±0.25)kg的为优等品,根据以上信息
完成下表:
解:(2)从优等品数量的角度看,因A种技术种植的西瓜优等品数量较多,所以A种技术较好;从平均数的角度看,因A种技术种植的西瓜质量的平均数更接近5kg,所以A种技术较好;
从方差的角度看,因B种技术种植的西瓜质量的方差更小,所以B种技术种植的西瓜质量更为稳定;
从市场销售角度看,因优等品更畅销,A种技术种植的西瓜优等品数量更多,且平均质量更接近5kg,因而更适合推广A种技术.
即学即练
(2)请分别从优等品数量、平均数与方差三方面对A,B两种技术做出评价;从市场销售的角度看,你认为推广哪种种植技术较好?
数据收集—数据整理—数据描述—数据分析
数据的
集中趋势
数据的
波动程度
方差
用样本平均数
估计总体平均数
用样本方差
估计总体方差
平均数
中位数
众 数
用样本估计总体
课堂小结
1.已知数据x1,x2,…,xn的平均数是2,则一组新数据x1+8,x2+8,…,xn+8的平均数是_______.
2.七(1)班四个绿化小组植树的棵树如下:10,10,x,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是______棵.
3.数据2,3,x,4的平均数是3,则这组数据的众数是________.
10
11
3
强化训练
4.对甲、乙两台机床生产的零件进行抽样测量,其平均数都是10,机床甲的方差0.02,机床乙的方差0.06,由此可知:_____(填“甲”或“乙”)机床性能较好
甲
强化训练
5.某制鞋厂准备生产一批男皮鞋,随机选出120名中年男子进行调查,得知所需鞋号的中位数是24 cm,众数是25 cm,平均数是24 cm,则下列说法正确的是( )
A.所需27 cm的鞋的人数太少,所以可以不生产
B.因为平均数为24,故这批男鞋只生产24 cm的鞋
C.因为中位数是24,故24 cm的鞋的生产量应占首位
D.因为众数是25,故25 cm的鞋的生产量要占首位
D
强化训练
6.为了从甲、乙两名学生中选拔一人参加全市初中数学联赛,对他们进行了5次测验,成绩如下:
甲:65 80 80 85 90
乙:70 90 85 75 80
(1)分别求出甲、乙两名学生5次测验成绩的平均数及方差;
(2)如果你是他们的辅导老师,应派哪名学生参加这次数学联赛?说明理由.
强化训练
(2) 分别计算成绩的平均数 和方差,填入表格. 若你是
老师,将小明与小亮的成绩
比较析后, 将分别给予他们
怎样的建议?
平均数 方差
小明
小亮
13.3
13.3
0.02
0.004
强化训练
解:从平均数看,两人的平均水平相同;从方差看,小明的成绩较稳定,小亮的成绩波动较大.
给小明的建议是:加强锻炼,提高爆发力,提升短跑成绩;
给小亮的建议是:总结经验,找出成绩忽高忽低的原因,在稳定中提高.
平均数 方差
小明
小亮
13.3
13.3
0.02
0.004
强化训练
7.为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如图所示的统计图,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为____,图①中m的值为____;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
40
15
解:(2)这组样本数据的众数为35号,中位数为36号
(3)200×30%=60(双)
强化训练
8.A,B农场养奶牛200头,为了了解两奶牛场一天牛奶的产量,各随意抽取5头奶牛,称得它们的牛奶产量(单位:千克)如下:
A农场:6.3,6.9,6.5,7.9,7.4;
B农场:6.8,7.3,7.5,6.6,6.8.
(1)分别计算5头奶牛牛奶产量的平均数,估计A,B两农场中200头奶牛一天的牛奶产量;
(2)如果学校要实行“学生奶工程”,你认为选择哪个农场作为学校的长期供货方较好?
强化训练
解:(1)A农场5头奶牛牛奶产量的平均数为7千克,估计A农场200头奶牛一天的牛奶产量为7×200=1400(千克).B农场5头奶牛牛奶产量的平均数为7千克,估计B农场200头奶牛一天的牛奶产量为7×200=1400(千克) (2)A农场5头奶牛牛奶产量的方差为0.344,B农场5头奶牛牛奶产量的方差为0.116,因为0.344> 0.116,所以B农场奶牛的产量相对稳定,因此选择B农场作为供货方
强化训练
9.甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图①、图②所示的统计图
(1)在图②中画出折线表示乙队在集训期间内这五场比赛成绩的变化情况;
(2)已知甲队五场比赛成绩的平均分x甲=90分,请你计算乙队五场比赛成绩的平均分x乙;
(3)就这五场比赛,分别计算两队成绩的方差;
(4)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和方差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
强化训练
解:(1)图略 (2)x乙=90分 (3)甲队成绩的方差是41.2,乙队成绩的方差是111.6 (4)从平均分看,两队的平均分相同,实力大体相当;从折线的趋势看,甲队比赛成绩呈上升趋势,而乙队比赛成绩呈下降趋势;从获胜场数看,甲队胜三场,乙队胜两场,甲队成绩较好;从方差看,甲队比赛成绩比乙队比赛成绩波动小,甲队成绩较稳定.综上所述,选派甲队参赛更能取得好成绩
强化训练
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
