人教版七年级数学下册5.3.1 平行线的性质学案( 第1课时含答案)
文档属性
| 名称 | 人教版七年级数学下册5.3.1 平行线的性质学案( 第1课时含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 179.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 00:00:00 | ||
图片预览

文档简介
第5章 相交线与平行线
5.3.1 平行线的性质
第1课时 平行线的性质
核心提要
平行线的性质:
(1)两直线平行,同位角________.
(2)两直线平行,内错角________.
(3)两直线平行,同旁内角________ .
典例精讲
知识点1:两直线平行,同位角相等
1.如图,AD平分∠EAC,AD∥BC.求证:∠B=∠1.
知识点2:两直线平行,内错角相等
2.如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为________.
知识点3:两直线平行,同旁内角互补
3.如图,直线a、b被c所截,且a∥b,∠1=120°,则∠2=________.
变式训练
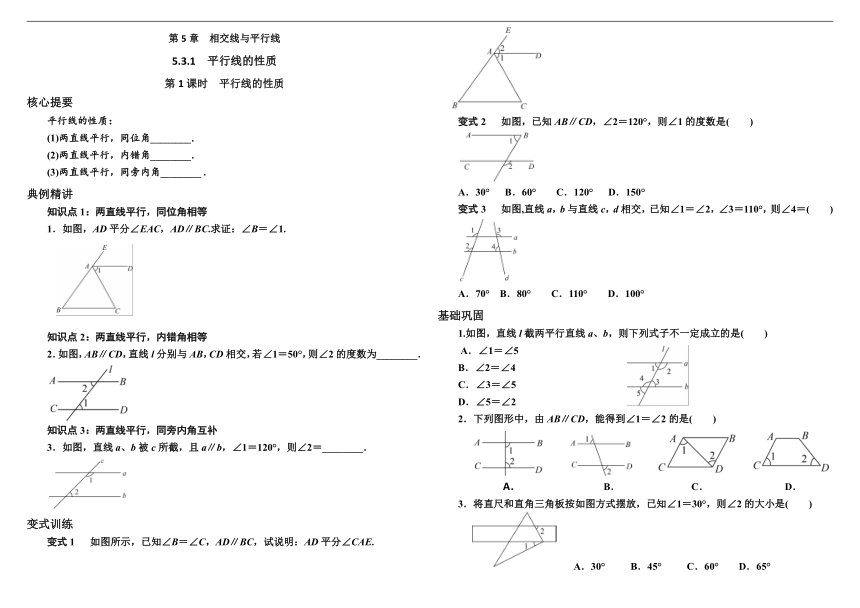
变式1? 如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
变式2? 如图,已知AB∥CD,∠2=120°,则∠1的度数是( )
A.30° B.60° C.120° D.150°
变式3? 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
A.70° B.80° C.110° D.100°
基础巩固
1.如图,直线l截两平行直线a、b,则下列式子不一定成立的是( )
A.∠1=∠5
B.∠2=∠4
C.∠3=∠5
D.∠5=∠2
2.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
B. C. D.
3.将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
A.30° B.45° C.60° D.65°
4.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
5.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是________.
6.如图,已知∠1=∠2,∠D=55°,求∠B的度数.
能力提升
7.如图,已知AB∥CD,BC∥DE,则∠B+∠D的度数为( )
A.180° B.90° C.120° D.不确定
8.如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C=________.
9.如图,AB∥CD,∠B=160°,∠D=120°,则∠E=________
10.已知,如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.
培优训练
11.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
解:∵EF∥AD(已知),
∴∠2= ________( ).
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换).
∴AB∥________( ).
∴∠BAC+________=180°( ).
∵∠BAC=70°,
∴∠AGD=________.
第1课时 平行线的性质----答案
【核心提要】
(1)相等 (2)相等 (3)互补
【典例精讲】
1.证明:∵AD平分∠EAC,
∴∠EAD=∠1.
∵AD∥BC,
∴∠EAD=∠B,
∴∠B=∠1.
2.50° 3.60°
【变式训练】
1.解:∵AD∥BC,
∴∠2=∠B,∠1=∠C.
又∵∠B=∠C,
∴∠1=∠2,
即AD平分∠CAE.
2.B 3.A
【基础巩固】
1.D 2.B 3.C 4.C 5.60°
6.解:∵∠1=∠2,∠2=∠EQD,
∴∠1=∠EQD,
∴AB∥CD.
∴∠B+∠D=180°.
∵∠D=55°,∴∠B=125°.
【能力提升】
7.A 8.120° 9.40°
10.解:∵AB∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠ABE=∠DCF(已知),
∴∠EBC=∠FCB,
∴BE∥CF(内错角相等,两直线平行),
∴∠E=∠F(两直线平行,内错角相等).
【培优训练】
11.∠3 两直线平行,同位角相等
DG 内错角相等,两直线平行
∠DGA 两直线平行,同旁内角互补 110°
5.3.1 平行线的性质
第1课时 平行线的性质
核心提要
平行线的性质:
(1)两直线平行,同位角________.
(2)两直线平行,内错角________.
(3)两直线平行,同旁内角________ .
典例精讲
知识点1:两直线平行,同位角相等
1.如图,AD平分∠EAC,AD∥BC.求证:∠B=∠1.
知识点2:两直线平行,内错角相等
2.如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为________.
知识点3:两直线平行,同旁内角互补
3.如图,直线a、b被c所截,且a∥b,∠1=120°,则∠2=________.
变式训练
变式1? 如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
变式2? 如图,已知AB∥CD,∠2=120°,则∠1的度数是( )
A.30° B.60° C.120° D.150°
变式3? 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
A.70° B.80° C.110° D.100°
基础巩固
1.如图,直线l截两平行直线a、b,则下列式子不一定成立的是( )
A.∠1=∠5
B.∠2=∠4
C.∠3=∠5
D.∠5=∠2
2.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
B. C. D.
3.将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
A.30° B.45° C.60° D.65°
4.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
5.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是________.
6.如图,已知∠1=∠2,∠D=55°,求∠B的度数.
能力提升
7.如图,已知AB∥CD,BC∥DE,则∠B+∠D的度数为( )
A.180° B.90° C.120° D.不确定
8.如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C=________.
9.如图,AB∥CD,∠B=160°,∠D=120°,则∠E=________
10.已知,如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.
培优训练
11.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
解:∵EF∥AD(已知),
∴∠2= ________( ).
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换).
∴AB∥________( ).
∴∠BAC+________=180°( ).
∵∠BAC=70°,
∴∠AGD=________.
第1课时 平行线的性质----答案
【核心提要】
(1)相等 (2)相等 (3)互补
【典例精讲】
1.证明:∵AD平分∠EAC,
∴∠EAD=∠1.
∵AD∥BC,
∴∠EAD=∠B,
∴∠B=∠1.
2.50° 3.60°
【变式训练】
1.解:∵AD∥BC,
∴∠2=∠B,∠1=∠C.
又∵∠B=∠C,
∴∠1=∠2,
即AD平分∠CAE.
2.B 3.A
【基础巩固】
1.D 2.B 3.C 4.C 5.60°
6.解:∵∠1=∠2,∠2=∠EQD,
∴∠1=∠EQD,
∴AB∥CD.
∴∠B+∠D=180°.
∵∠D=55°,∴∠B=125°.
【能力提升】
7.A 8.120° 9.40°
10.解:∵AB∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠ABE=∠DCF(已知),
∴∠EBC=∠FCB,
∴BE∥CF(内错角相等,两直线平行),
∴∠E=∠F(两直线平行,内错角相等).
【培优训练】
11.∠3 两直线平行,同位角相等
DG 内错角相等,两直线平行
∠DGA 两直线平行,同旁内角互补 110°
