人教版七年级数学下册 第五章 5.3 平行线的性质 复习教案(表格式)
文档属性
| 名称 | 人教版七年级数学下册 第五章 5.3 平行线的性质 复习教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 35.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 10:20:09 | ||
图片预览


文档简介
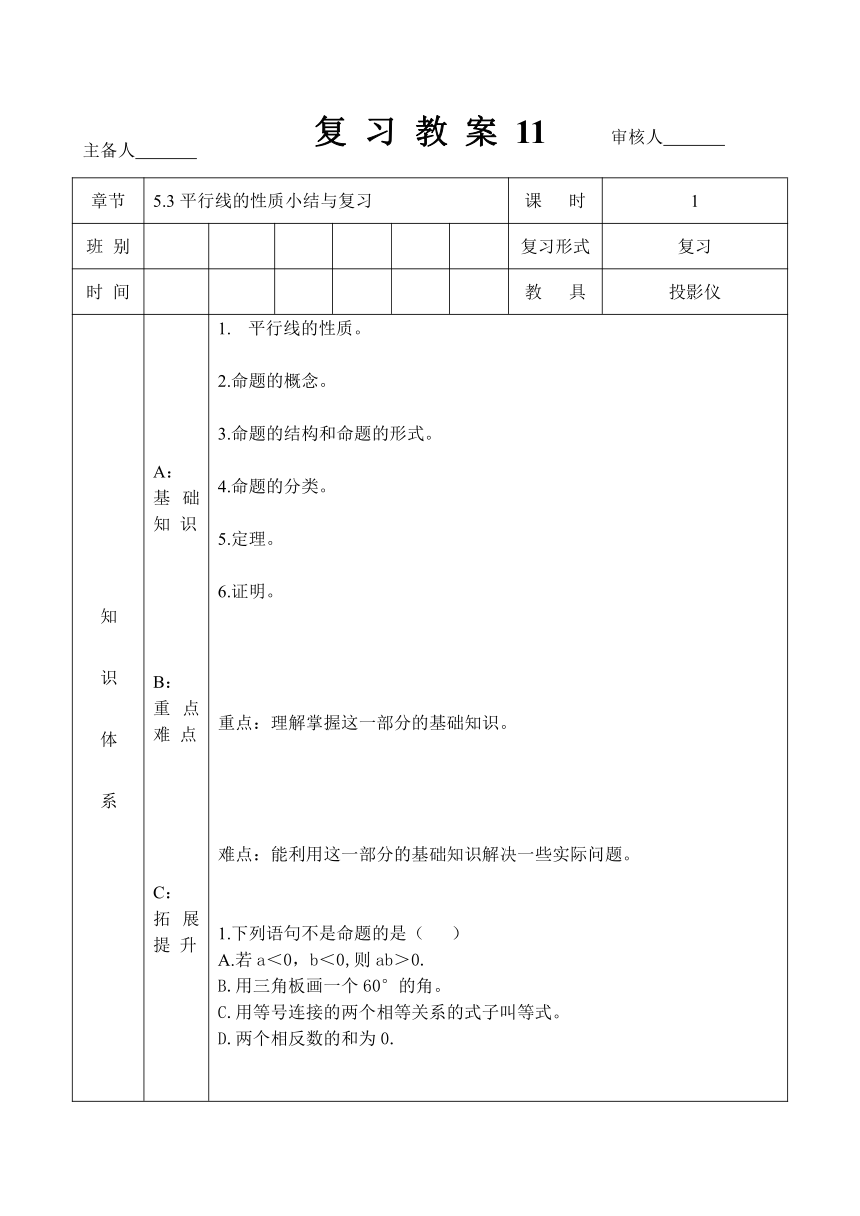
复 习 教 案 11
章节 5.3平行线的性质小结与复习 课 时 1
班 别 复习形式 复习
时 间 教 具 投影仪
知 识 体 系 A: 基础知 识 B: 重点难 点 C: 拓展提 升 平行线的性质。 2.命题的概念。 3.命题的结构和命题的形式。 4.命题的分类。 5.定理。 6.证明。 重点:理解掌握这一部分的基础知识。 难点:能利用这一部分的基础知识解决一些实际问题。 1.下列语句不是命题的是( ) A.若a<0,b<0,则ab>0. B.用三角板画一个60°的角。 C.用等号连接的两个相等关系的式子叫等式。 D.两个相反数的和为0.
具 体 内 容 备 注
2.下列命题中,真命题是( ) A.同位角互补。 B.同旁内角互补,两直线平行。 C.内错角相等。 D.两个锐角的补角相等。 3.命题“垂直于同一直线的两直线平行”可以写成“如果 ( )那么( )。 4.梯形的两个下底角分别是100°和80°.求梯形两个上底角的度数。 5.(1)已知a∥b,∠2=100°,求∠1,∠3,∠4的度数。 (2)已知∠2=100°,∠4=80°,判断 a,b之间的位置关系。 6..指出下列命题的题设和结论。 (1)对顶角相等。 (2)两直线平行,内错角相等。 (3)同角的补角相等。 (4)同旁内角相等,两直线平行。 (5)如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
具 体 内 容 备 注
7.AB∥CD,∠A=∠C,试判断AD与BC的位置关系?为什么? 8.已知直线b∥c,a⊥b,求证a⊥c. 9.判断下列命题是真命题还是假命题,如果是假命题,举出一个反例。 (1)同旁内角相等。 (2)两个锐角的和是100°.(3)邻补角是互补的角。(4)互补的角是邻补角。(5)对顶角相等。(6)过一点有且只有一条直线和已知直线平行。 10.写出下列文字命题的证明过程(要求:画出图形,写出已知、求证及证明) 求证两条平行被第三条直线所截,构成的一对同位角的平分线互相平行。
质 疑 问 难 1.你还有那些不懂得问题 2.质疑问难,互帮互学
重 塑 结 构 总 结 提 升(结构图表) 5.3平行线的性质练习课 1.平行线的性质。 2.命题的概念。 3.命题的结构和命题的形式。 4.命题的分类。 5.定理。 6.证明。
布 置 作 业 归纳整理这一部分的基础知识
学校 检查 记实
听 课 意 见
审核人
主备人
章节 5.3平行线的性质小结与复习 课 时 1
班 别 复习形式 复习
时 间 教 具 投影仪
知 识 体 系 A: 基础知 识 B: 重点难 点 C: 拓展提 升 平行线的性质。 2.命题的概念。 3.命题的结构和命题的形式。 4.命题的分类。 5.定理。 6.证明。 重点:理解掌握这一部分的基础知识。 难点:能利用这一部分的基础知识解决一些实际问题。 1.下列语句不是命题的是( ) A.若a<0,b<0,则ab>0. B.用三角板画一个60°的角。 C.用等号连接的两个相等关系的式子叫等式。 D.两个相反数的和为0.
具 体 内 容 备 注
2.下列命题中,真命题是( ) A.同位角互补。 B.同旁内角互补,两直线平行。 C.内错角相等。 D.两个锐角的补角相等。 3.命题“垂直于同一直线的两直线平行”可以写成“如果 ( )那么( )。 4.梯形的两个下底角分别是100°和80°.求梯形两个上底角的度数。 5.(1)已知a∥b,∠2=100°,求∠1,∠3,∠4的度数。 (2)已知∠2=100°,∠4=80°,判断 a,b之间的位置关系。 6..指出下列命题的题设和结论。 (1)对顶角相等。 (2)两直线平行,内错角相等。 (3)同角的补角相等。 (4)同旁内角相等,两直线平行。 (5)如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
具 体 内 容 备 注
7.AB∥CD,∠A=∠C,试判断AD与BC的位置关系?为什么? 8.已知直线b∥c,a⊥b,求证a⊥c. 9.判断下列命题是真命题还是假命题,如果是假命题,举出一个反例。 (1)同旁内角相等。 (2)两个锐角的和是100°.(3)邻补角是互补的角。(4)互补的角是邻补角。(5)对顶角相等。(6)过一点有且只有一条直线和已知直线平行。 10.写出下列文字命题的证明过程(要求:画出图形,写出已知、求证及证明) 求证两条平行被第三条直线所截,构成的一对同位角的平分线互相平行。
质 疑 问 难 1.你还有那些不懂得问题 2.质疑问难,互帮互学
重 塑 结 构 总 结 提 升(结构图表) 5.3平行线的性质练习课 1.平行线的性质。 2.命题的概念。 3.命题的结构和命题的形式。 4.命题的分类。 5.定理。 6.证明。
布 置 作 业 归纳整理这一部分的基础知识
学校 检查 记实
听 课 意 见
审核人
主备人
