2020年华师大新版数学下册七年级《第7章 一次方程组》单元测试卷(解析版)
文档属性
| 名称 | 2020年华师大新版数学下册七年级《第7章 一次方程组》单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 412.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 00:00:00 | ||
图片预览




文档简介
2020年华师大新版数学下册七年级《第7章 一次方程组》单元测试卷
一.选择题(共12小题)
1.以下方程中,是二元一次方程的是( )
A.8x﹣y=y B.xy=3 C.3x+2y=3z D.y=
2.方程kx+3y=5有一组解是,则k的值是( )
A.1 B.﹣1 C.0 D.2
3.二元一次方程x+y=5有( )个解.
A.1 B.2 C.3 D.无数
4.若甲数为x,乙数为y,则“甲数的3倍比乙数的一半少2”列成方程就是( )
A.3x+y=2 B.3x﹣y=2 C. y﹣3x=2 D. y+2=3x
5.某校七年级一班有x人,分y小组进行课外兴趣活动,若每组6人,则余4人,若每组7人,则不足5人,则全班的人数为( )
A.60人 B.58人 C.62人 D.59人
6.下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
7.如果方程x﹣y=3与下面方程中的一个组成的方程组的解为,那么这个方程可以是( )
A.3x﹣4y=16 B. x+2y=5 C. x+3y=8 D.2(x﹣y)=6y?
8.在等式y=kx+b中,当x=2时,y=﹣4;当x=﹣2时,y=8,则这个等式是( )
A.y=3x+2 B.y=﹣3x+2 C.y=3x﹣2 D.y=﹣3x﹣2
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
10.如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( )
A.3元,3.5元 B.3.5元,3元 C.4元,4.5元 D.4.5元,4元
11.下列方程组中,与方程组的解不同的方程组是( )
A. B.
C. D.
12.已知a+b=16,b+c=12,c+a=10,则a+b+c等于( )
A.19 B.38 C.14 D.22
二.填空题(共8小题)
13.如果2x2a﹣b﹣1﹣3y3a+2b﹣16=10是一个二元一次方程,那么数a= ,b= .
14.写出一个解是的二元一次方程是 .
15.已知方程2x﹣y=1,用含x的代数式表示y,得 .
16.如图所示的各图表示由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数为s,按此规律推断,以s,n为未知数的二元一次方程为s= .
17.小明家准备春节前举行80人的聚餐,需要去某餐馆订餐.据了解餐馆有10人坐和8人坐两种餐桌,要使所订的每个餐桌刚好坐满,则订餐方案共有 种.
18.若方程组是关于x,y的二元一次方程组,则代数式a+b+c的值是 .
19.已知方程组的解满足x+y=2,则k的值为 .
20.定义运算“※”,规定x※y=ax2+by,其中a,b为常数,且1※2=5,2※1=6,则2※3= .
三.解答题(共8小题)
21.已知和都是方程y=ax+b的解,求a和b的值.
22.(开放题)是否存在整数m,使关于x的方程2x+9=2﹣(m﹣2)x在整数范围内有解,你能找到几个m的值?你能求出相应的x的解吗?
23.阅读下列材料,解答下面的问题:
我们知道方程2x+3y=12有无数个解,但在实际生活中我们往往只需求出其正整数解.
例:由2x+3y=12,得:y=,根据x、y为正整数,运用尝试法可以知道方程2x+3y=12的正整数解为.
问题:
(1)请你直接写出方程3x﹣y=6的一组正整数解 .
(2)若为自然数,则满足条件的正整数x的值有 个.
A.5 B.6 C.7 D.8
(3)七年级某班为了奖励学生学习的进步,购买单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费48元,问有哪几种购买方案?
24.已知关于x,y的方程组和的解相同,求(2a﹣b)2的值.
25.解方程组:.
26.《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文.甲、乙两人原来各有多少钱?
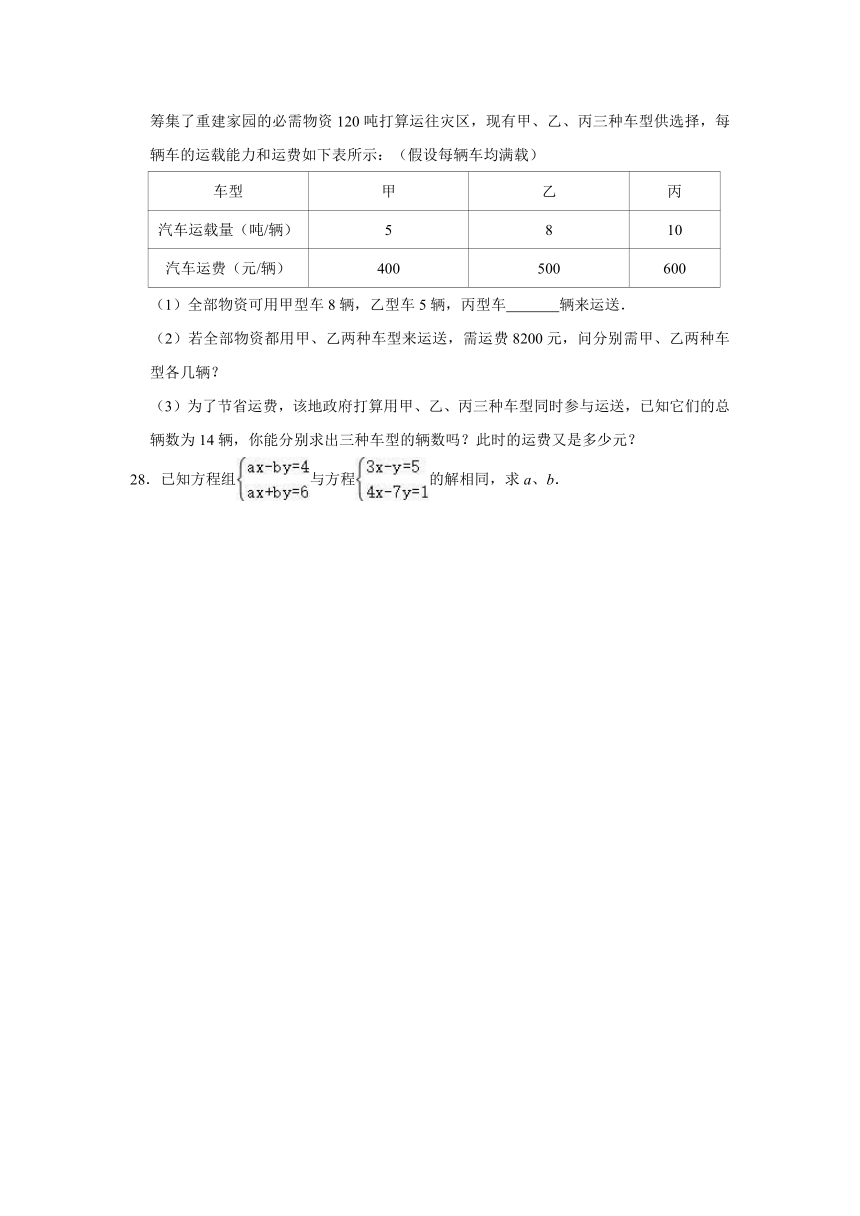
27.雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 甲 乙 丙
汽车运载量(吨/辆) 5 8 10
汽车运费(元/辆) 400 500 600
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
28.已知方程组与方程的解相同,求a、b.
2020年华师大新版数学下册七年级《第7章 一次方程组》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.以下方程中,是二元一次方程的是( )
A.8x﹣y=y B.xy=3 C.3x+2y=3z D.y=
【分析】根据二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程进行分析即可.
【解答】解:A、8x﹣y=y是二元一次方程;
B、xy=3是二元二次方程;
C、3x+2y=3z是三元一次方程;
D、y=是分式方程.
故选:A.
【点评】此题主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
2.方程kx+3y=5有一组解是,则k的值是( )
A.1 B.﹣1 C.0 D.2
【分析】知道了方程的解,可以把这组解代入方程,得到一个含有未知数k的一元一次方程,从而可以求出k的值.
【解答】解:把是代入方程kx+3y=5中,得
2k+3=5,
解得k=1.
故选:A.
【点评】本题考查了二元一次方程的解,解题关键是把方程的解代入原方程,使原方程转化为以系数k为未知数的方程.
3.二元一次方程x+y=5有( )个解.
A.1 B.2 C.3 D.无数
【分析】根据二元一次方程有无数个解即可得到结果.
【解答】解:方程x+y=5有无数个解.
故选:D.
【点评】此题考查了解二元一次方程,解题的关键是将y看做已知数求出x.
4.若甲数为x,乙数为y,则“甲数的3倍比乙数的一半少2”列成方程就是( )
A.3x+y=2 B.3x﹣y=2 C. y﹣3x=2 D. y+2=3x
【分析】因为“甲数的3倍比乙数的一半少2”,则可列成方程y﹣3x=2.
【解答】解:若甲数为x,乙数为y,可列方程为y﹣3x=2.
故选:C.
【点评】此题比较容易,根据“甲数的3倍比乙数的一半少2”可以直接列方程.
5.某校七年级一班有x人,分y小组进行课外兴趣活动,若每组6人,则余4人,若每组7人,则不足5人,则全班的人数为( )
A.60人 B.58人 C.62人 D.59人
【分析】根据每组的不同人数分别表示出班级人数x,再由两个方程建立方程组求出其解即可.
【解答】解:由题意,得
,
解得:.
故选:B.
【点评】本题考查了数学分组问题的运用,列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,解答时根据兴趣小组的人数之和等于全班人数建立方程是关键.
6.下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
【分析】根据二元一次方程组的定义解答判断即可.
【解答】解:A、,有三个未知数,错误;
B、xy的未知数的次数是2,错误;
C、符合二元一次方程组的定义,正确;
D、不是整式方程,错误;
故选:C.
【点评】此题考查二元一次方程组,关键是根据二元一次方程组定义判断.
7.如果方程x﹣y=3与下面方程中的一个组成的方程组的解为,那么这个方程可以是( )
A.3x﹣4y=16 B. x+2y=5 C. x+3y=8 D.2(x﹣y)=6y?
【分析】把已知方程与各项方程联立组成方程组,使其解为x=4,y=1即可.
【解答】解:A、联立得:,
解得:,不合题意;
B、联立得:,
解得:,不合题意;
C、联立得:,
解得:,不合题意;
D、联立得:,
解得:,符合题意.
故选:D.
【点评】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.
8.在等式y=kx+b中,当x=2时,y=﹣4;当x=﹣2时,y=8,则这个等式是( )
A.y=3x+2 B.y=﹣3x+2 C.y=3x﹣2 D.y=﹣3x﹣2
【分析】分别把当x=2时,y=﹣4,当x=﹣2时,y=8代入等式,得到关于k、b的二元一次方程组,求出k、b的值即可.
【解答】解:分别把当x=2时,y=﹣4,当x=﹣2时,y=8代入等式y=kx+b得,
,
①﹣②得,4k=﹣12,
解得k=﹣3,
把k=﹣3代入①得,﹣4=﹣3×2+b,
解得b=2,
分别把k=﹣3,b=2的值代入等式y=kx+b得,y=﹣3x+2,
故选:B.
【点评】本题主要考查的是解二元一次方程组的加减消元法和代入消元法,难度适中.
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
【分析】设该店有客房x间,房客y人;根据题意一房七客多七客,一房九客一房空得出方程组即可.
【解答】解:设该店有客房x间,房客y人;
根据题意得:,
故选:A.
【点评】本题考查了二元一次方程组的应用;根据题意得出方程组是解决问题的关键.
10.如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( )
A.3元,3.5元 B.3.5元,3元 C.4元,4.5元 D.4.5元,4元
【分析】设1听果奶为x元,1听可乐y元,由题意可得等量关系:①1听果奶的费用+4听可乐的费用=17元,②1听可乐的费用﹣1听果奶的费用=0.5元,根据等量关系列出方程组,再解即可.
【解答】解:设1听果奶为x元,1听可乐y元,由题意得:
,
解得:,
故选:A.
【点评】此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程组.
11.下列方程组中,与方程组的解不同的方程组是( )
A. B.
C. D.
【分析】将方程组的解代入各选项中进行比对,看方程组中的两个方程是否成立,就可找出答案.
【解答】解:方程组的解为,将此解分别代入四个方程组:
A、代入后方程成立,故正确;
B、代入后方程成立,故正确;
C、代入后方程(1)成立,方程(2)不成立,故错误;
D、代入后方程成立,故正确.
故选:C.
【点评】先求出题目给出的方程组的解,然后依次代入各选项进行验证,选出符合条件的选项.
12.已知a+b=16,b+c=12,c+a=10,则a+b+c等于( )
A.19 B.38 C.14 D.22
【分析】把三个方程相加得到2a+2b+2c=38,然后两边除以2即可得到a+b+c的值.
【解答】解:,
①+②+③得2a+2b+2c=38,
所以a+b+c=19.
故选:A.
【点评】本题考查了解三元一次方程组:利用加减消元或代入消元把解三元一次方程组的问题转化为解二元一次方程组.
二.填空题(共8小题)
13.如果2x2a﹣b﹣1﹣3y3a+2b﹣16=10是一个二元一次方程,那么数a= 3 ,b= 4 .
【分析】根据一元二次方程的定义,令未知数的次数为1,即可列方程解答.
【解答】解:∵2x2a﹣b﹣1﹣3y3a+2b﹣16=10是一个二元一次方程,
∴,
解得,,
故答案为3,4.
【点评】本题考查了二元一次方程的定义,根据题意列出方程是解题的关键.
14.写出一个解是的二元一次方程是 x+y=3.(答案不唯一) .
【分析】要用已知的解构成一个二元一次方程,可以利用方程的解构造一个等式,然后将数值换成未知数即可.
【解答】解:如2+1=3,∵x=2,y=1,
∴换成未知数为x+y=3.(答案不唯一)
故答案为:x+y=3.(答案不唯一)
【点评】此题是解二元一次方程的逆过程,是结论开放性题目.二元一次方程是不定方程,一个二元一次方程可以有无数组解,一组解也可以构造无数个二元一次方程.
不定方程:所谓不定方程是指解的范围为整数、正整数、有理数或代数整数的方程或方程组,其未知数的个数通常多于方程的个数.
15.已知方程2x﹣y=1,用含x的代数式表示y,得 y=2x﹣1 .
【分析】要把方程2x﹣y=1,用含x的代数式表示y,就要把方程中含有y的项移到方程的左边,其它的项移到方程的右边,再进一步合并同类项、系数化为1即可.
【解答】解:移项,得﹣y=1﹣2x,
系数化1,得y=2x﹣1.
故填y=2x﹣1.
【点评】此题考查了方程的灵活变形,熟悉移项、合并同类项、系数化为1的步骤.
16.如图所示的各图表示由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数为s,按此规律推断,以s,n为未知数的二元一次方程为s= 3(n﹣1) .
【分析】由图可知:
第一图:有花盆3个,每条边有花盆2个,那么s=3;
第二图:有花盆6个,每条边有花盆3个,那么s=3×2;
第三图:有花盆9个,每条边有花盆4个,那么s=3×3;
…
由此可知以s,n为未知数的二元一次方程为s=3(n﹣1).
【解答】解:根据图案组成的是三角形的形状,则其周长等于边长的3倍,
所以s=3(n﹣1).
故答案为:3(n﹣1).
【点评】本题要注意给出的图片中所包含的规律,然后根据规律列出方程.
17.小明家准备春节前举行80人的聚餐,需要去某餐馆订餐.据了解餐馆有10人坐和8人坐两种餐桌,要使所订的每个餐桌刚好坐满,则订餐方案共有 3 种.
【分析】根据题意列出二元一次方程,根据方程的解为整数讨论得到订餐方案即可.
【解答】解:设10人桌x张,8人桌y张,根据题意得:10x+8y=80
∵x、y均为整数,
∴,,
共三种方案.
故答案为:3.
【点评】本题考查了二元一次方程的应用,二元一次方程有无数个解,当都为整数时,变为有数个解.
18.若方程组是关于x,y的二元一次方程组,则代数式a+b+c的值是 ﹣2或﹣3 .
【分析】根据二元一次方程组的定义:
(1)含有两个未知数;
(2)含有未知数的项的次数都是1.
【解答】解:若方程组是关于x,y的二元一次方程组,
则c+3=0,a﹣2=1,b+3=1,
解得c=﹣3,a=3,b=﹣2.
所以代数式a+b+c的值是﹣2.
或c+3=0,a﹣2=0,b+3=1,
解得c=﹣3,a=2,b=﹣2.
所以代数式a+b+c的值是﹣3.
故答案为:﹣2或﹣3.
【点评】本题主要考查了二元一次方程组的定义,利用它的定义即可求出代数式的解.
19.已知方程组的解满足x+y=2,则k的值为 2 .
【分析】方程组两方程相加表示出x+y,代入x+y=2中求出k的值即可.
【解答】解:,
①+②得:3(x+y)=k+4,即x+y=,
代入x+y=2中得:k+4=6,
解得:k=2,
故答案为:2
【点评】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
20.定义运算“※”,规定x※y=ax2+by,其中a,b为常数,且1※2=5,2※1=6,则2※3= 10 .
【分析】已知等式利用新定义化简求出a与b的值,原式计算即可得到结果.
【解答】解:根据题意得:,
解得:,
则2※3=4+6=10.
故答案为:10
【点评】此题考查了解二元一次方程组,弄清题中的新定义是解本题的关键.
三.解答题(共8小题)
21.已知和都是方程y=ax+b的解,求a和b的值.
【分析】把两组解分别代入方程,得关于a,b的方程组,求解即可.
【解答】解:把和代入方程y=ax+b得,
,
解得a=1,b=1.
【点评】此题主要考查了二元一次方程解的定义以及解二元一次方程组的基本方法.
22.(开放题)是否存在整数m,使关于x的方程2x+9=2﹣(m﹣2)x在整数范围内有解,你能找到几个m的值?你能求出相应的x的解吗?
【分析】要求关于x的方程2x+9=2﹣(m﹣2)x在整数范围内有解,首先要解这个方程,其解x=,根据题意的要求让其为整数,故m的值只能为±1,±7.
【解答】解:存在,四组.
∵原方程可变形为﹣mx=7,
∴当m=1时,x=﹣7;
m=﹣1时,x=7;
m=7时,x=﹣1;
m=﹣7时,x=1.
【点评】此题只需把m当成字母已知数求解,然后根据条件的限制进行分析求解.
23.阅读下列材料,解答下面的问题:
我们知道方程2x+3y=12有无数个解,但在实际生活中我们往往只需求出其正整数解.
例:由2x+3y=12,得:y=,根据x、y为正整数,运用尝试法可以知道方程2x+3y=12的正整数解为.
问题:
(1)请你直接写出方程3x﹣y=6的一组正整数解 .
(2)若为自然数,则满足条件的正整数x的值有 B 个.
A.5 B.6 C.7 D.8
(3)七年级某班为了奖励学生学习的进步,购买单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费48元,问有哪几种购买方案?
【分析】根据题意可知,求方程的正整数解,先把方程做适当的变形,再列举正整数代入求解.
【解答】解:(1)由3x﹣y=6,得y=3x﹣6(x、y为正整数).
∵,
即x>2,
∴当x=3时,y=3;
即方程的正整数解是,
故答案为:;
(2)同样,若为自然数,
则有:0<x﹣3≤12,
即3<x≤15.
当x=4时,=12;
当x=5时,=6;
当x=6时,=4;
当x=7时,=3,
当x=9时,=2,
当x=15时,=1.
即满足条件x的值有6个,
故选B.
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=48,其中m、n均为自然数.
于是有:n=,
则有:,
解得:0<m<16.
由于n=为正整数,则48﹣3m为正整数,且为5的倍数.
∴当m=1时,n=9;
当m=6时,n=6,
当m=11时,n=3.
答:有三种购买方案:即购买单价为3元的笔记本1本,单价为5元的钢笔9支;
或购买单价为3元的笔记本6本,单价为5元的钢笔6支;
或购买单价为3元的笔记本11本,单价为5元的钢笔3支.
【点评】本题考查了二元一次方程组的应用,解题关键是要读懂题目给出的已知条件,根据条件求解.注意笔记本和钢笔是整体,所有不可能出现小数和负数,这也就说要求的是正整数.
24.已知关于x,y的方程组和的解相同,求(2a﹣b)2的值.
【分析】将两方程组中的第一个方程联立求出x与y的值,将第二个方程联立,把x与y的值代入求出a与b的值,进而求出所求式子的值.
【解答】解:由题意得:,
解得:,
代入,
解得:,
则(2a﹣b)2=[2×﹣(﹣)]2=4.
【点评】此题考查了二元一次方程组的解,方程组的解即为能使方程组两方程成立的未知数的值.也考查了解二元一次方程组以及代数式求值.
25.解方程组:.
【分析】先把方程组中的两方程去分母、去括号,再用加减消元法和代入消元法求解即可.
【解答】解:原方程组可化为,
∴,
(2)﹣(1),可得37y+74=0,
∴y=﹣2,
代入(1)得,8x﹣9×(﹣2)﹣6=0,
解得,x=﹣
故原方程组的解为.
【点评】此类题目比较简单,解答此题的关键是把方程组中的方程转化为不含分母及括号的方程,再利用解二元一次方程组的方法求解即可.
26.《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文.甲、乙两人原来各有多少钱?
【分析】根据甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文,可以列出方程组,从而可以解答本题.
【解答】解:设甲原有x文钱,乙原有y文钱,
由题意可得,,
解得:,
答:甲原有36文钱,乙原有24文钱.
【点评】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
27.雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 甲 乙 丙
汽车运载量(吨/辆) 5 8 10
汽车运费(元/辆) 400 500 600
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 4 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
【分析】(1)根据甲型车运载量是5吨/辆,乙型车运载量是8吨/辆,丙型车运载量是10吨/辆,再根据总吨数,即可求出丙型车的车辆数;
(2)设需甲车x辆,乙车y辆,根据运费8200元,总吨数是120,列出方程组,再进行求解即可;
(3)设甲车有a辆,乙车有b辆,则丙车有(14﹣a﹣b)辆,列出等式,再根据a、b、14﹣a﹣b均为正整数,求出a,b的值,从而得出答案.
【解答】解:(1)根据题意得:
(120﹣5×8﹣5×8)÷10=4(辆),
答:丙型车需4辆来运送.
故答案为:4.
(2)设需要甲x辆,乙y辆,根据题意得:
,
解得,
答:分别需甲、乙两种车型为8辆和10辆.
(3)设甲车有a辆,乙车有b辆,则丙车有(14﹣a﹣b)辆,由题意得
5a+8b+10(14﹣a﹣b)=120,
即a=4﹣b,
∵a、b、14﹣a﹣b均为正整数,
∴b只能等于5,从而a=2,14﹣a﹣b=7,
∴甲车2辆,乙车5辆,丙车7辆,
则需运费400×2+500×5+600×7=7500(元),
答:甲车2辆,乙车5辆,丙车7辆,需运费7500元.
【点评】本题考查了二元一次方程组和二元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题列出方程即可求解.利用整体思想和未知数的实际意义通过筛选法可得到未知数的具体解,这种方法要掌握.
28.已知方程组与方程的解相同,求a、b.
【分析】先求出已知方程组(2)的解,再代入方程组(1)即可求出a、b的值.
【解答】解:
①×7﹣②得:17x=34,
解得x=2.
把x=2代入①得:y=1.
所以第一个方程组的解是.
把x=2,y=1代入方程组得,
解得:;即a、b的值分别是2.5、1.
【点评】本题考查了同解方程组、解二元一次方程组.解答此题的关键是要弄清题意,方程组有相同的解及说明方程组(1)的解也适合(2),不要盲目求解,造成解题过程复杂化.
一.选择题(共12小题)
1.以下方程中,是二元一次方程的是( )
A.8x﹣y=y B.xy=3 C.3x+2y=3z D.y=
2.方程kx+3y=5有一组解是,则k的值是( )
A.1 B.﹣1 C.0 D.2
3.二元一次方程x+y=5有( )个解.
A.1 B.2 C.3 D.无数
4.若甲数为x,乙数为y,则“甲数的3倍比乙数的一半少2”列成方程就是( )
A.3x+y=2 B.3x﹣y=2 C. y﹣3x=2 D. y+2=3x
5.某校七年级一班有x人,分y小组进行课外兴趣活动,若每组6人,则余4人,若每组7人,则不足5人,则全班的人数为( )
A.60人 B.58人 C.62人 D.59人
6.下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
7.如果方程x﹣y=3与下面方程中的一个组成的方程组的解为,那么这个方程可以是( )
A.3x﹣4y=16 B. x+2y=5 C. x+3y=8 D.2(x﹣y)=6y?
8.在等式y=kx+b中,当x=2时,y=﹣4;当x=﹣2时,y=8,则这个等式是( )
A.y=3x+2 B.y=﹣3x+2 C.y=3x﹣2 D.y=﹣3x﹣2
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
10.如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( )
A.3元,3.5元 B.3.5元,3元 C.4元,4.5元 D.4.5元,4元
11.下列方程组中,与方程组的解不同的方程组是( )
A. B.
C. D.
12.已知a+b=16,b+c=12,c+a=10,则a+b+c等于( )
A.19 B.38 C.14 D.22
二.填空题(共8小题)
13.如果2x2a﹣b﹣1﹣3y3a+2b﹣16=10是一个二元一次方程,那么数a= ,b= .
14.写出一个解是的二元一次方程是 .
15.已知方程2x﹣y=1,用含x的代数式表示y,得 .
16.如图所示的各图表示由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数为s,按此规律推断,以s,n为未知数的二元一次方程为s= .
17.小明家准备春节前举行80人的聚餐,需要去某餐馆订餐.据了解餐馆有10人坐和8人坐两种餐桌,要使所订的每个餐桌刚好坐满,则订餐方案共有 种.
18.若方程组是关于x,y的二元一次方程组,则代数式a+b+c的值是 .
19.已知方程组的解满足x+y=2,则k的值为 .
20.定义运算“※”,规定x※y=ax2+by,其中a,b为常数,且1※2=5,2※1=6,则2※3= .
三.解答题(共8小题)
21.已知和都是方程y=ax+b的解,求a和b的值.
22.(开放题)是否存在整数m,使关于x的方程2x+9=2﹣(m﹣2)x在整数范围内有解,你能找到几个m的值?你能求出相应的x的解吗?
23.阅读下列材料,解答下面的问题:
我们知道方程2x+3y=12有无数个解,但在实际生活中我们往往只需求出其正整数解.
例:由2x+3y=12,得:y=,根据x、y为正整数,运用尝试法可以知道方程2x+3y=12的正整数解为.
问题:
(1)请你直接写出方程3x﹣y=6的一组正整数解 .
(2)若为自然数,则满足条件的正整数x的值有 个.
A.5 B.6 C.7 D.8
(3)七年级某班为了奖励学生学习的进步,购买单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费48元,问有哪几种购买方案?
24.已知关于x,y的方程组和的解相同,求(2a﹣b)2的值.
25.解方程组:.
26.《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文.甲、乙两人原来各有多少钱?
27.雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 甲 乙 丙
汽车运载量(吨/辆) 5 8 10
汽车运费(元/辆) 400 500 600
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
28.已知方程组与方程的解相同,求a、b.
2020年华师大新版数学下册七年级《第7章 一次方程组》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.以下方程中,是二元一次方程的是( )
A.8x﹣y=y B.xy=3 C.3x+2y=3z D.y=
【分析】根据二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程进行分析即可.
【解答】解:A、8x﹣y=y是二元一次方程;
B、xy=3是二元二次方程;
C、3x+2y=3z是三元一次方程;
D、y=是分式方程.
故选:A.
【点评】此题主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
2.方程kx+3y=5有一组解是,则k的值是( )
A.1 B.﹣1 C.0 D.2
【分析】知道了方程的解,可以把这组解代入方程,得到一个含有未知数k的一元一次方程,从而可以求出k的值.
【解答】解:把是代入方程kx+3y=5中,得
2k+3=5,
解得k=1.
故选:A.
【点评】本题考查了二元一次方程的解,解题关键是把方程的解代入原方程,使原方程转化为以系数k为未知数的方程.
3.二元一次方程x+y=5有( )个解.
A.1 B.2 C.3 D.无数
【分析】根据二元一次方程有无数个解即可得到结果.
【解答】解:方程x+y=5有无数个解.
故选:D.
【点评】此题考查了解二元一次方程,解题的关键是将y看做已知数求出x.
4.若甲数为x,乙数为y,则“甲数的3倍比乙数的一半少2”列成方程就是( )
A.3x+y=2 B.3x﹣y=2 C. y﹣3x=2 D. y+2=3x
【分析】因为“甲数的3倍比乙数的一半少2”,则可列成方程y﹣3x=2.
【解答】解:若甲数为x,乙数为y,可列方程为y﹣3x=2.
故选:C.
【点评】此题比较容易,根据“甲数的3倍比乙数的一半少2”可以直接列方程.
5.某校七年级一班有x人,分y小组进行课外兴趣活动,若每组6人,则余4人,若每组7人,则不足5人,则全班的人数为( )
A.60人 B.58人 C.62人 D.59人
【分析】根据每组的不同人数分别表示出班级人数x,再由两个方程建立方程组求出其解即可.
【解答】解:由题意,得
,
解得:.
故选:B.
【点评】本题考查了数学分组问题的运用,列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,解答时根据兴趣小组的人数之和等于全班人数建立方程是关键.
6.下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
【分析】根据二元一次方程组的定义解答判断即可.
【解答】解:A、,有三个未知数,错误;
B、xy的未知数的次数是2,错误;
C、符合二元一次方程组的定义,正确;
D、不是整式方程,错误;
故选:C.
【点评】此题考查二元一次方程组,关键是根据二元一次方程组定义判断.
7.如果方程x﹣y=3与下面方程中的一个组成的方程组的解为,那么这个方程可以是( )
A.3x﹣4y=16 B. x+2y=5 C. x+3y=8 D.2(x﹣y)=6y?
【分析】把已知方程与各项方程联立组成方程组,使其解为x=4,y=1即可.
【解答】解:A、联立得:,
解得:,不合题意;
B、联立得:,
解得:,不合题意;
C、联立得:,
解得:,不合题意;
D、联立得:,
解得:,符合题意.
故选:D.
【点评】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.
8.在等式y=kx+b中,当x=2时,y=﹣4;当x=﹣2时,y=8,则这个等式是( )
A.y=3x+2 B.y=﹣3x+2 C.y=3x﹣2 D.y=﹣3x﹣2
【分析】分别把当x=2时,y=﹣4,当x=﹣2时,y=8代入等式,得到关于k、b的二元一次方程组,求出k、b的值即可.
【解答】解:分别把当x=2时,y=﹣4,当x=﹣2时,y=8代入等式y=kx+b得,
,
①﹣②得,4k=﹣12,
解得k=﹣3,
把k=﹣3代入①得,﹣4=﹣3×2+b,
解得b=2,
分别把k=﹣3,b=2的值代入等式y=kx+b得,y=﹣3x+2,
故选:B.
【点评】本题主要考查的是解二元一次方程组的加减消元法和代入消元法,难度适中.
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
【分析】设该店有客房x间,房客y人;根据题意一房七客多七客,一房九客一房空得出方程组即可.
【解答】解:设该店有客房x间,房客y人;
根据题意得:,
故选:A.
【点评】本题考查了二元一次方程组的应用;根据题意得出方程组是解决问题的关键.
10.如图所示,小刚手拿20元钱正在和售货员对话,请你仔细看图,1听果奶、1听可乐的单价分别是( )
A.3元,3.5元 B.3.5元,3元 C.4元,4.5元 D.4.5元,4元
【分析】设1听果奶为x元,1听可乐y元,由题意可得等量关系:①1听果奶的费用+4听可乐的费用=17元,②1听可乐的费用﹣1听果奶的费用=0.5元,根据等量关系列出方程组,再解即可.
【解答】解:设1听果奶为x元,1听可乐y元,由题意得:
,
解得:,
故选:A.
【点评】此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程组.
11.下列方程组中,与方程组的解不同的方程组是( )
A. B.
C. D.
【分析】将方程组的解代入各选项中进行比对,看方程组中的两个方程是否成立,就可找出答案.
【解答】解:方程组的解为,将此解分别代入四个方程组:
A、代入后方程成立,故正确;
B、代入后方程成立,故正确;
C、代入后方程(1)成立,方程(2)不成立,故错误;
D、代入后方程成立,故正确.
故选:C.
【点评】先求出题目给出的方程组的解,然后依次代入各选项进行验证,选出符合条件的选项.
12.已知a+b=16,b+c=12,c+a=10,则a+b+c等于( )
A.19 B.38 C.14 D.22
【分析】把三个方程相加得到2a+2b+2c=38,然后两边除以2即可得到a+b+c的值.
【解答】解:,
①+②+③得2a+2b+2c=38,
所以a+b+c=19.
故选:A.
【点评】本题考查了解三元一次方程组:利用加减消元或代入消元把解三元一次方程组的问题转化为解二元一次方程组.
二.填空题(共8小题)
13.如果2x2a﹣b﹣1﹣3y3a+2b﹣16=10是一个二元一次方程,那么数a= 3 ,b= 4 .
【分析】根据一元二次方程的定义,令未知数的次数为1,即可列方程解答.
【解答】解:∵2x2a﹣b﹣1﹣3y3a+2b﹣16=10是一个二元一次方程,
∴,
解得,,
故答案为3,4.
【点评】本题考查了二元一次方程的定义,根据题意列出方程是解题的关键.
14.写出一个解是的二元一次方程是 x+y=3.(答案不唯一) .
【分析】要用已知的解构成一个二元一次方程,可以利用方程的解构造一个等式,然后将数值换成未知数即可.
【解答】解:如2+1=3,∵x=2,y=1,
∴换成未知数为x+y=3.(答案不唯一)
故答案为:x+y=3.(答案不唯一)
【点评】此题是解二元一次方程的逆过程,是结论开放性题目.二元一次方程是不定方程,一个二元一次方程可以有无数组解,一组解也可以构造无数个二元一次方程.
不定方程:所谓不定方程是指解的范围为整数、正整数、有理数或代数整数的方程或方程组,其未知数的个数通常多于方程的个数.
15.已知方程2x﹣y=1,用含x的代数式表示y,得 y=2x﹣1 .
【分析】要把方程2x﹣y=1,用含x的代数式表示y,就要把方程中含有y的项移到方程的左边,其它的项移到方程的右边,再进一步合并同类项、系数化为1即可.
【解答】解:移项,得﹣y=1﹣2x,
系数化1,得y=2x﹣1.
故填y=2x﹣1.
【点评】此题考查了方程的灵活变形,熟悉移项、合并同类项、系数化为1的步骤.
16.如图所示的各图表示由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数为s,按此规律推断,以s,n为未知数的二元一次方程为s= 3(n﹣1) .
【分析】由图可知:
第一图:有花盆3个,每条边有花盆2个,那么s=3;
第二图:有花盆6个,每条边有花盆3个,那么s=3×2;
第三图:有花盆9个,每条边有花盆4个,那么s=3×3;
…
由此可知以s,n为未知数的二元一次方程为s=3(n﹣1).
【解答】解:根据图案组成的是三角形的形状,则其周长等于边长的3倍,
所以s=3(n﹣1).
故答案为:3(n﹣1).
【点评】本题要注意给出的图片中所包含的规律,然后根据规律列出方程.
17.小明家准备春节前举行80人的聚餐,需要去某餐馆订餐.据了解餐馆有10人坐和8人坐两种餐桌,要使所订的每个餐桌刚好坐满,则订餐方案共有 3 种.
【分析】根据题意列出二元一次方程,根据方程的解为整数讨论得到订餐方案即可.
【解答】解:设10人桌x张,8人桌y张,根据题意得:10x+8y=80
∵x、y均为整数,
∴,,
共三种方案.
故答案为:3.
【点评】本题考查了二元一次方程的应用,二元一次方程有无数个解,当都为整数时,变为有数个解.
18.若方程组是关于x,y的二元一次方程组,则代数式a+b+c的值是 ﹣2或﹣3 .
【分析】根据二元一次方程组的定义:
(1)含有两个未知数;
(2)含有未知数的项的次数都是1.
【解答】解:若方程组是关于x,y的二元一次方程组,
则c+3=0,a﹣2=1,b+3=1,
解得c=﹣3,a=3,b=﹣2.
所以代数式a+b+c的值是﹣2.
或c+3=0,a﹣2=0,b+3=1,
解得c=﹣3,a=2,b=﹣2.
所以代数式a+b+c的值是﹣3.
故答案为:﹣2或﹣3.
【点评】本题主要考查了二元一次方程组的定义,利用它的定义即可求出代数式的解.
19.已知方程组的解满足x+y=2,则k的值为 2 .
【分析】方程组两方程相加表示出x+y,代入x+y=2中求出k的值即可.
【解答】解:,
①+②得:3(x+y)=k+4,即x+y=,
代入x+y=2中得:k+4=6,
解得:k=2,
故答案为:2
【点评】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
20.定义运算“※”,规定x※y=ax2+by,其中a,b为常数,且1※2=5,2※1=6,则2※3= 10 .
【分析】已知等式利用新定义化简求出a与b的值,原式计算即可得到结果.
【解答】解:根据题意得:,
解得:,
则2※3=4+6=10.
故答案为:10
【点评】此题考查了解二元一次方程组,弄清题中的新定义是解本题的关键.
三.解答题(共8小题)
21.已知和都是方程y=ax+b的解,求a和b的值.
【分析】把两组解分别代入方程,得关于a,b的方程组,求解即可.
【解答】解:把和代入方程y=ax+b得,
,
解得a=1,b=1.
【点评】此题主要考查了二元一次方程解的定义以及解二元一次方程组的基本方法.
22.(开放题)是否存在整数m,使关于x的方程2x+9=2﹣(m﹣2)x在整数范围内有解,你能找到几个m的值?你能求出相应的x的解吗?
【分析】要求关于x的方程2x+9=2﹣(m﹣2)x在整数范围内有解,首先要解这个方程,其解x=,根据题意的要求让其为整数,故m的值只能为±1,±7.
【解答】解:存在,四组.
∵原方程可变形为﹣mx=7,
∴当m=1时,x=﹣7;
m=﹣1时,x=7;
m=7时,x=﹣1;
m=﹣7时,x=1.
【点评】此题只需把m当成字母已知数求解,然后根据条件的限制进行分析求解.
23.阅读下列材料,解答下面的问题:
我们知道方程2x+3y=12有无数个解,但在实际生活中我们往往只需求出其正整数解.
例:由2x+3y=12,得:y=,根据x、y为正整数,运用尝试法可以知道方程2x+3y=12的正整数解为.
问题:
(1)请你直接写出方程3x﹣y=6的一组正整数解 .
(2)若为自然数,则满足条件的正整数x的值有 B 个.
A.5 B.6 C.7 D.8
(3)七年级某班为了奖励学生学习的进步,购买单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费48元,问有哪几种购买方案?
【分析】根据题意可知,求方程的正整数解,先把方程做适当的变形,再列举正整数代入求解.
【解答】解:(1)由3x﹣y=6,得y=3x﹣6(x、y为正整数).
∵,
即x>2,
∴当x=3时,y=3;
即方程的正整数解是,
故答案为:;
(2)同样,若为自然数,
则有:0<x﹣3≤12,
即3<x≤15.
当x=4时,=12;
当x=5时,=6;
当x=6时,=4;
当x=7时,=3,
当x=9时,=2,
当x=15时,=1.
即满足条件x的值有6个,
故选B.
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=48,其中m、n均为自然数.
于是有:n=,
则有:,
解得:0<m<16.
由于n=为正整数,则48﹣3m为正整数,且为5的倍数.
∴当m=1时,n=9;
当m=6时,n=6,
当m=11时,n=3.
答:有三种购买方案:即购买单价为3元的笔记本1本,单价为5元的钢笔9支;
或购买单价为3元的笔记本6本,单价为5元的钢笔6支;
或购买单价为3元的笔记本11本,单价为5元的钢笔3支.
【点评】本题考查了二元一次方程组的应用,解题关键是要读懂题目给出的已知条件,根据条件求解.注意笔记本和钢笔是整体,所有不可能出现小数和负数,这也就说要求的是正整数.
24.已知关于x,y的方程组和的解相同,求(2a﹣b)2的值.
【分析】将两方程组中的第一个方程联立求出x与y的值,将第二个方程联立,把x与y的值代入求出a与b的值,进而求出所求式子的值.
【解答】解:由题意得:,
解得:,
代入,
解得:,
则(2a﹣b)2=[2×﹣(﹣)]2=4.
【点评】此题考查了二元一次方程组的解,方程组的解即为能使方程组两方程成立的未知数的值.也考查了解二元一次方程组以及代数式求值.
25.解方程组:.
【分析】先把方程组中的两方程去分母、去括号,再用加减消元法和代入消元法求解即可.
【解答】解:原方程组可化为,
∴,
(2)﹣(1),可得37y+74=0,
∴y=﹣2,
代入(1)得,8x﹣9×(﹣2)﹣6=0,
解得,x=﹣
故原方程组的解为.
【点评】此类题目比较简单,解答此题的关键是把方程组中的方程转化为不含分母及括号的方程,再利用解二元一次方程组的方法求解即可.
26.《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文.甲、乙两人原来各有多少钱?
【分析】根据甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文,可以列出方程组,从而可以解答本题.
【解答】解:设甲原有x文钱,乙原有y文钱,
由题意可得,,
解得:,
答:甲原有36文钱,乙原有24文钱.
【点评】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
27.雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 甲 乙 丙
汽车运载量(吨/辆) 5 8 10
汽车运费(元/辆) 400 500 600
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 4 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
【分析】(1)根据甲型车运载量是5吨/辆,乙型车运载量是8吨/辆,丙型车运载量是10吨/辆,再根据总吨数,即可求出丙型车的车辆数;
(2)设需甲车x辆,乙车y辆,根据运费8200元,总吨数是120,列出方程组,再进行求解即可;
(3)设甲车有a辆,乙车有b辆,则丙车有(14﹣a﹣b)辆,列出等式,再根据a、b、14﹣a﹣b均为正整数,求出a,b的值,从而得出答案.
【解答】解:(1)根据题意得:
(120﹣5×8﹣5×8)÷10=4(辆),
答:丙型车需4辆来运送.
故答案为:4.
(2)设需要甲x辆,乙y辆,根据题意得:
,
解得,
答:分别需甲、乙两种车型为8辆和10辆.
(3)设甲车有a辆,乙车有b辆,则丙车有(14﹣a﹣b)辆,由题意得
5a+8b+10(14﹣a﹣b)=120,
即a=4﹣b,
∵a、b、14﹣a﹣b均为正整数,
∴b只能等于5,从而a=2,14﹣a﹣b=7,
∴甲车2辆,乙车5辆,丙车7辆,
则需运费400×2+500×5+600×7=7500(元),
答:甲车2辆,乙车5辆,丙车7辆,需运费7500元.
【点评】本题考查了二元一次方程组和二元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题列出方程即可求解.利用整体思想和未知数的实际意义通过筛选法可得到未知数的具体解,这种方法要掌握.
28.已知方程组与方程的解相同,求a、b.
【分析】先求出已知方程组(2)的解,再代入方程组(1)即可求出a、b的值.
【解答】解:
①×7﹣②得:17x=34,
解得x=2.
把x=2代入①得:y=1.
所以第一个方程组的解是.
把x=2,y=1代入方程组得,
解得:;即a、b的值分别是2.5、1.
【点评】本题考查了同解方程组、解二元一次方程组.解答此题的关键是要弄清题意,方程组有相同的解及说明方程组(1)的解也适合(2),不要盲目求解,造成解题过程复杂化.
