2020年华师大新版数学下册八年级《第17章 函数及其图象》单元测试卷(解析版)
文档属性
| 名称 | 2020年华师大新版数学下册八年级《第17章 函数及其图象》单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 475.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 00:00:00 | ||
图片预览


文档简介
2020年华师大新版数学下册八年级《第17章 函数及其图象》单元测试卷
一.选择题(共12小题)
1.已知y轴上的点P到原点的距离为5,则点P的坐标为( )
A.(5,0) B.(0,5)或(0,﹣5)
C.(0,5) D.(5,0)或(﹣5,0)
2.已知点P(m,1)在第二象限,则点Q(﹣m,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,若象棋盘上建立直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),那么“炮”位于点( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,2) D.(1,﹣2)
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
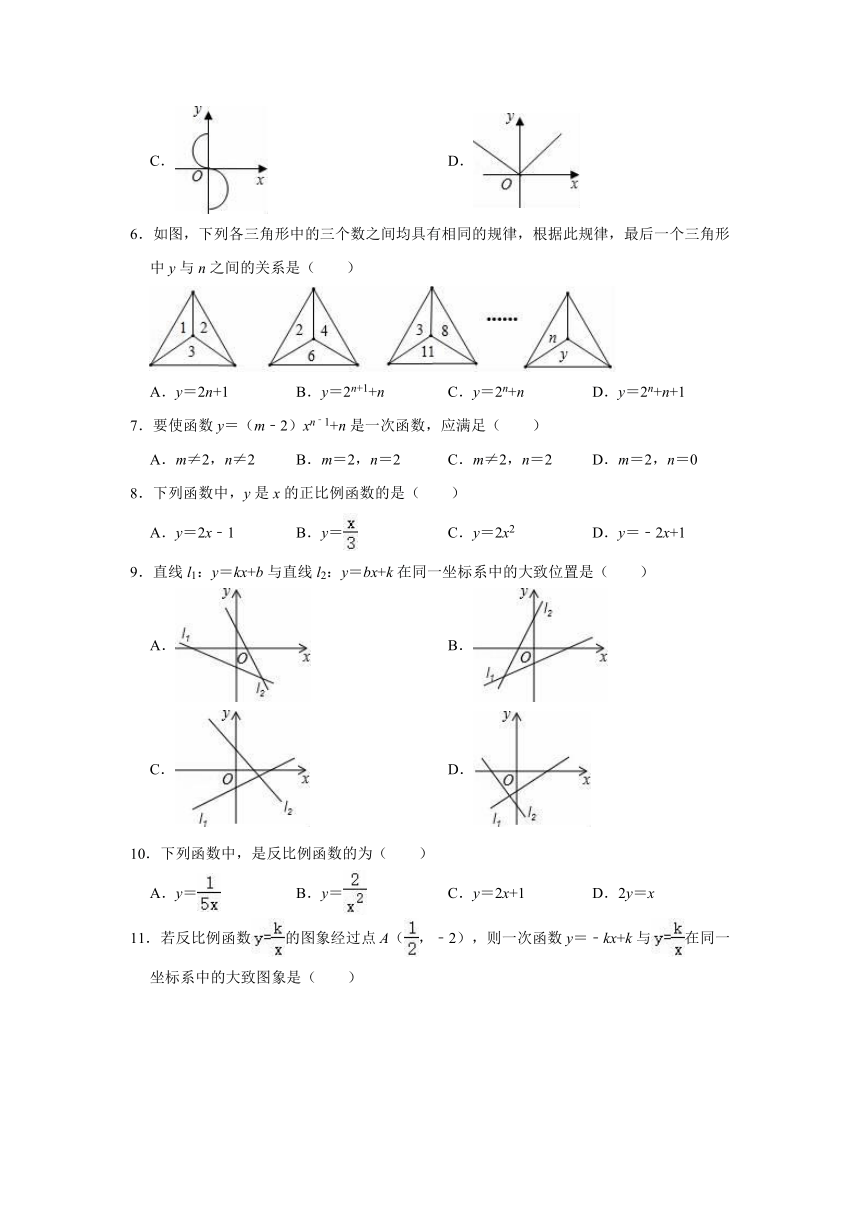
5.下列各图中反映了变量y是x的函数是( )
A. B.
C. D.
6.如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+1+n C.y=2n+n D.y=2n+n+1
7.要使函数y=(m﹣2)xn﹣1+n是一次函数,应满足( )
A.m≠2,n≠2 B.m=2,n=2 C.m≠2,n=2 D.m=2,n=0
8.下列函数中,y是x的正比例函数的是( )
A.y=2x﹣1 B.y= C.y=2x2 D.y=﹣2x+1
9.直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A. B.
C. D.
10.下列函数中,是反比例函数的为( )
A.y= B.y= C.y=2x+1 D.2y=x
11.若反比例函数的图象经过点A(,﹣2),则一次函数y=﹣kx+k与在同一坐标系中的大致图象是( )
A. B.
C. D.
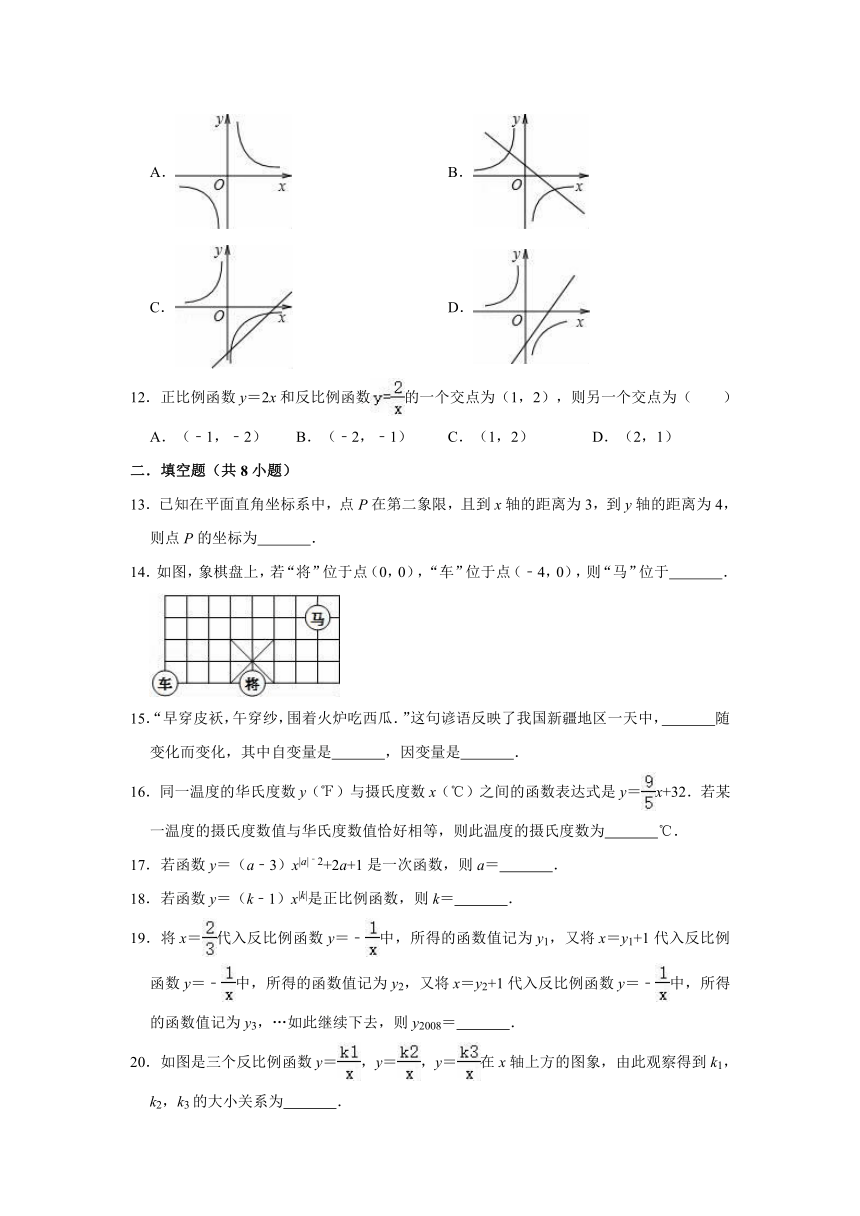
12.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
二.填空题(共8小题)
13.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 .
14.如图,象棋盘上,若“将”位于点(0,0),“车”位于点(﹣4,0),则“马”位于 .
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 随 变化而变化,其中自变量是 ,因变量是 .
16.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ℃.
17.若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= .
18.若函数y=(k﹣1)x|k|是正比例函数,则k= .
19.将x=代入反比例函数y=﹣中,所得的函数值记为y1,又将x=y1+1代入反比例函数y=﹣中,所得的函数值记为y2,又将x=y2+1代入反比例函数y=﹣中,所得的函数值记为y3,…如此继续下去,则y2008= .
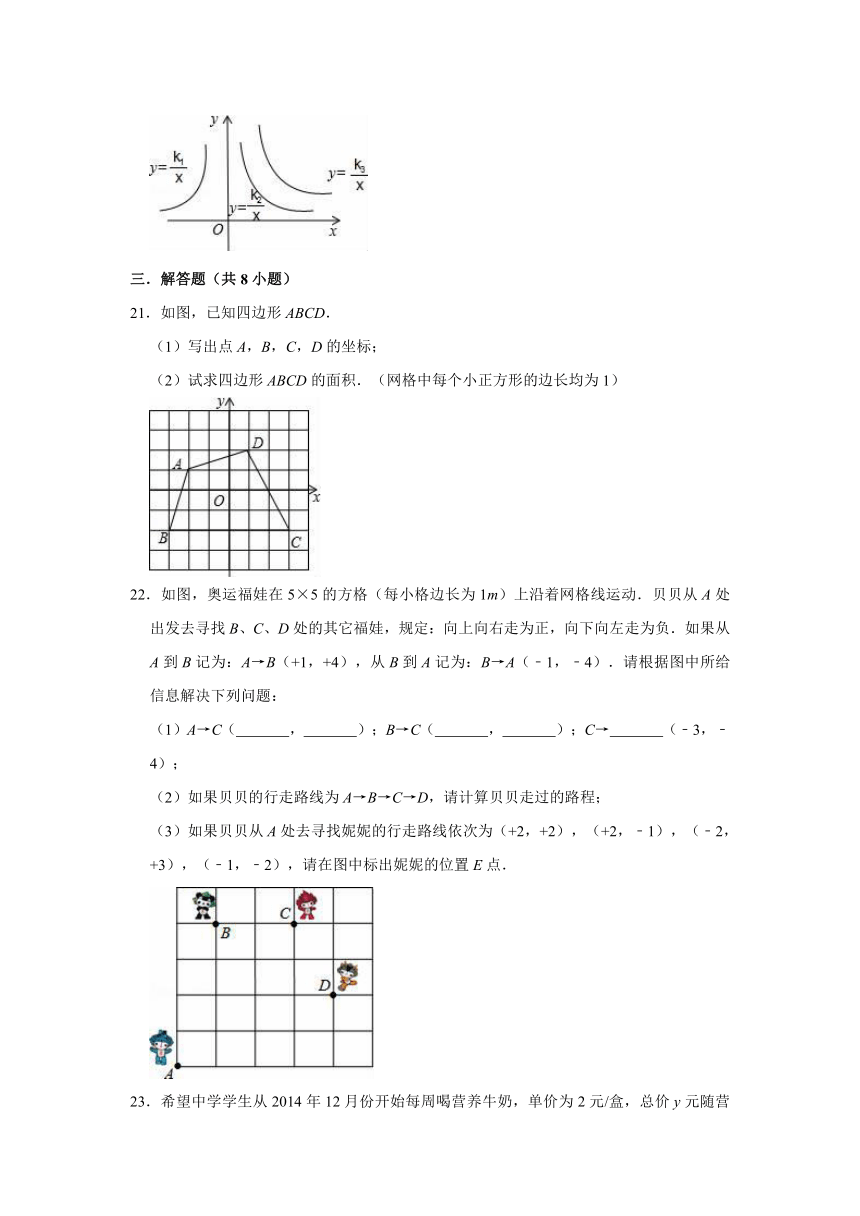
20.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 .
三.解答题(共8小题)
21.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
22.如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4).请根据图中所给信息解决下列问题:
(1)A→C( , );B→C( , );C→ (﹣3,﹣4);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出妮妮的位置E点.
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
24.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 ;
②该函数的一条性质: .
25.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
26.已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
27.有这样一个问题:探究函数y=的图象与性质.小美根据学习函数的经验,对函数y=的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x ﹣2 ﹣ ﹣1 ﹣ 1 2 3 4 …
y 0 ﹣ ﹣1 ﹣ m …
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质: .
28.已知反比例函数y=,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
2020年华师大新版数学下册八年级《第17章 函数及其图象》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.已知y轴上的点P到原点的距离为5,则点P的坐标为( )
A.(5,0) B.(0,5)或(0,﹣5)
C.(0,5) D.(5,0)或(﹣5,0)
【分析】首先根据点在y轴上,确定点P的横坐标为0,再根据P到原点的距离为5,确定P点的纵坐标,要注意分两情况考虑才不漏解,P可能在原点上方,也可能在原点下方.
【解答】解:由题中y轴上的点P得知:P点的横坐标为0;
∵点P到原点的距离为5,
∴点P的纵坐标为±5,
所以点P的坐标为(0,5)或(0,﹣5).
故选:B.
【点评】此题主要考查了由点到原点的距离确定点的坐标,要注意点在坐标轴上时,点到原点的距离要分两种情况考虑.
2.已知点P(m,1)在第二象限,则点Q(﹣m,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据第二象限内点的横坐标是负数判断出m<0,再根据各象限内点的坐标特征解答.
【解答】解:∵点P(m,1)在第二象限,
∴m<0,
∴﹣m>0,
∴点Q(﹣m,3)在第一象限.
故选:A.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
3.如图,若象棋盘上建立直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),那么“炮”位于点( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,2) D.(1,﹣2)
【分析】先利用“象”所在点的坐标画出直角坐标系,然后写出“炮”所在点的坐标即可.
【解答】解:如图,“炮”位于点(﹣1,1).
故选:B.
【点评】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
【分析】根据自变量、因变量的含义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【解答】解:∵在这个变化中,自变量是温度,因变量是声速,
∴选项A正确;
∵根据数据表,可得温度越高,声速越快,
∴选项B正确;
∵342×5=1710(m),
∴当空气温度为20℃时,声音5s可以传播1710m,
∴选项C错误;
∵324﹣318=6(m/s),330﹣324=6(m/s),336﹣330=6(m/s),342﹣336=6(m/s),348﹣342=6(m/s),
∴当温度每升高10℃,声速增加6m/s,
∴选项D正确.
故选:C.
【点评】此题主要考查了自变量、因变量的含义和判断,要熟练掌握.
5.下列各图中反映了变量y是x的函数是( )
A. B.
C. D.
【分析】函数的意义反映在图象上简单的判断方法是:做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,
只有D正确.
故选:D.
【点评】本题主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
6.如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+1+n C.y=2n+n D.y=2n+n+1
【分析】根据题意得:第1个图:y=1+2,第2个图:y=2+4=2+22,第3个图:y=3+8=3+23,…以此类推第n个图:y=n+2n,即可得到答案.
【解答】解:根据题意得:
第1个图:y=1+2,
第2个图:y=2+4=2+22,
第3个图:y=3+8=3+23,
…
以此类推
第n个图:y=n+2n,
故选:C.
【点评】本题考查了函数关系式和规律型:图形的变化类,正确找出规律,进行猜想归纳即可.
7.要使函数y=(m﹣2)xn﹣1+n是一次函数,应满足( )
A.m≠2,n≠2 B.m=2,n=2 C.m≠2,n=2 D.m=2,n=0
【分析】根据y=kx+b(k、b是常数,k≠0)是一次函数,可得m﹣2≠0,n﹣1=1,可得答案.
【解答】解:∵y=(m﹣2)xn﹣1+n是一次函数,
∴m﹣2≠0,n﹣1=1,
∴m≠2,n=2,
故选:C.
【点评】本题考查了一次函数,y=kx+b,k、b是常数,k≠0,x的次数等于1是解题关键.
8.下列函数中,y是x的正比例函数的是( )
A.y=2x﹣1 B.y= C.y=2x2 D.y=﹣2x+1
【分析】根据正比例函数的定义:一般地,两个变量x,y之间的关系式可以表示成形如y=kx(k为常数,且k≠0)的函数,那么y就叫做x的正比例函数.
【解答】解:根据正比例函数的定义可知选B.
故选:B.
【点评】主要考查正比例函数的定义:一般地,两个变量x,y之间的关系式可以表示成形如y=kx(k为常数,且k≠0)的函数,那么y就叫做x的正比例函数.
9.直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A. B.
C. D.
【分析】根据一次函数的系数与图象的关系依次分析选项,找k、b取值范围相同的即得答案.
【解答】解:根据一次函数的系数与图象的关系依次分析选项可得:
A、由图可得,y1=kx+b中,k<0,b<0,y2=bx+k中,b>0,k<0,b、k的取值矛盾,故本选项错误;
B、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b>0,k>0,b的取值相矛盾,故本选项错误;
C、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b<0,k>0,k的取值相一致,故本选项正确;
D、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b<0,k<0,k的取值相矛盾,故本选项错误;
故选:C.
【点评】本题主要考查了一次函数的图象性质,要掌握它们的性质才能灵活解题.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.
10.下列函数中,是反比例函数的为( )
A.y= B.y= C.y=2x+1 D.2y=x
【分析】根据反比例函数的定义回答即可.
【解答】解:A、是反比例函数,故A符合题意;
B、不是反比例函数,故B不符合题意;
C、是一次函数,故C不符合题意;
D、是正比例函数,故D不符合题意.
故选:A.
【点评】本题主要考查的是反比例函数的定义,掌握反比例函数的定义是解题的关键.
11.若反比例函数的图象经过点A(,﹣2),则一次函数y=﹣kx+k与在同一坐标系中的大致图象是( )
A. B.
C. D.
【分析】首先利用待定系数法算出反比例函数k的值,再根据k的值确定反比例函数所在象限,根据k的值确定一次函数解析式,根据一次函数解析式确定一次函数图象所在象限,即可选出答案.
【解答】解:∵反比例函数的图象经过点A(,﹣2),
∴k=×(﹣2)=﹣1,
∴反比例函数解析式为:y=﹣,
∴图象过第二、四象限,
∵k=﹣1,
∴一次函数y=x﹣1,
∴图象经过第一、三、四象限,
联立两函数解析式可得:﹣=x﹣1,
则x2﹣x+1=0,
∵△=1﹣4<0,
∴两函数图象无交点,
故选:D.
【点评】此题主要考查了待定系数法求反比例函数解析式,以及一次函数与反比例函数图象的性质,关键是根据k的值正确确定函数图象所在象限.
12.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
【分析】根据反比例函数的关于原点对称的性质知,正比例函数y=2x和反比例函数的另一个交点与点(1,2)关于原点对称.
【解答】解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
【点评】本题考查了反比例函数图象的对称性.关于原点对称的两点的横纵坐标互为相反数.
二.填空题(共8小题)
13.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 (﹣4,3) .
【分析】根据第二象限点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
【解答】解:∵点P在第二象限,且到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标为﹣4,纵坐标为3,
∴点P的坐标为(﹣4,3).
故答案为:(﹣4,3).
【点评】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.
14.如图,象棋盘上,若“将”位于点(0,0),“车”位于点(﹣4,0),则“马”位于 (3,3) .
【分析】根据已知两点的坐标建立坐标系,然后确定其它点的坐标.
【解答】解:结合图形以“将”(0,0)作为基准点,则“马”位于(0+3,0+3),
即(3,3).
故答案为:(3,3).
【点评】此题主要考查了点的坐标确定位置,解决此类问题需要先确定原点的位置,再求未知点的位置.或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 温度 随 时间 变化而变化,其中自变量是 时间 ,因变量是 温度 .
【分析】根据函数的定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应;来解答即可.
【解答】解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
【点评】函数的定义:设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数,记作y=f(x);变量是指在程序的运行过程中随时可以发生变化的量.
16.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ﹣40 ℃.
【分析】根据题意得x+32=x,解方程即可求得x的值.
【解答】解:根据题意得x+32=x,
解得x=﹣40.
故答案是:﹣40.
【点评】本题考查了函数的关系式,根据摄氏度数值与华氏度数值恰好相等转化为解方程问题是关键.
17.若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= ﹣3 .
【分析】根据一次函数的定义得到a=±3,且a≠3即可得到答案.
【解答】解:∵函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,
∴a=±3,
又∵a≠3,
∴a=﹣3.
故答案为:﹣3.
【点评】本题考查了一次函数的定义:对于y=kx+b(k、b为常数,k≠0),y称为x的一次函数.
18.若函数y=(k﹣1)x|k|是正比例函数,则k= ﹣1 .
【分析】根据正比例函数的定义,可得k﹣1≠0,|k|=1,从而求出k值.
【解答】解:∵根据正比例函数的定义,
可得:k﹣1≠0,|k|=1,
∴k=﹣1.
故答案为:﹣1.
【点评】考查了正比例函数的定义,解题关键是掌握正比例函数的定义条件,正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.
19.将x=代入反比例函数y=﹣中,所得的函数值记为y1,又将x=y1+1代入反比例函数y=﹣中,所得的函数值记为y2,又将x=y2+1代入反比例函数y=﹣中,所得的函数值记为y3,…如此继续下去,则y2008= ﹣ .
【分析】分别计算出y1,y2,y3,y4,可得到每三个一循环,而2008=669×3…1,即可得到y2008=y1,继而得出答案.
【解答】解:当x=时,y1=﹣;
当x=﹣+1=﹣时,y2=2,
当x=2+1=3时,y3=﹣,
当x=﹣+1=时,y4=﹣;
按照规律,y5=2,…,我们发现,y的值三个一循环20,8÷3=669…1,
∴y2008=y1=﹣.
故答案为:﹣.
【点评】本题考查了反比例函数的定义,按照题目的叙述计算一下y的值,从中观察得到规律,是解决本题的关键.
20.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 k1<k2<k3 .
【分析】本题考查反比例函数与的图象特点.
【解答】解:读图可知:三个反比例函数y=的图象在第二象限;故k1<0;y=,y=在第一象限;且y=的图象距原点较远,故有:k1<k2<k3;综合可得:k1<k2<k3.故填k1<k2<k3.
【点评】反比例函数y=的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.且图象距原点越远,k的绝对值越大.
三.解答题(共8小题)
21.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
【分析】(1)根据各点所在的象限,对应的横坐标、纵坐标,分别写出点的坐标;
(2)首先把四边形ABCD分割成规则图形,再求其面积和即可.
【解答】解:(1)A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
【点评】此题主要考查了点的坐标,以及求不规则图形的面积,关键是把不规则的图形正确的分割成规则图形.
22.如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4).请根据图中所给信息解决下列问题:
(1)A→C( +3 , +4 );B→C( +2 , 0 );C→ A (﹣3,﹣4);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出妮妮的位置E点.
【分析】(1)根据标记的第一个数字表示左、右方向,第二个数字表示上、下方向依次写出即可;
(2)根据运动路线列式计算即可得解;
(3)在图中依次表示出各位置,然后确定出点E的位置即可.
【解答】解:(1)A→C(+3,+4);B→C(+2,0);C→A (﹣3,﹣4);
故答案为:+3,+4;+2,0;A;
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
根据题意得:|+1|+|+4|+|+2|+|0|+|+1|+|﹣2|=10m.
(3)妮妮的位置E点如图所示.
【点评】本题考查了坐标确定位置,读懂题目信息,理解标记的两个数的实际意义是解题的关键.
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
【分析】根据总价=单价×数量,可得函数关系式.
【解答】解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
【点评】主要考查了常量与变量.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
24.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 2 ;
②该函数的一条性质: 该函数有最大值 .
【分析】(1)按照自变量由小到大,利用平滑的曲线连结各点即可;
(2)①在所画的函数图象上找出自变量为4所对应的函数值即可;
②利用函数图象有最高点求解.
【解答】解:(1)如图,
(2)①x=4对应的函数值y约为2.0;
②该函数有最大值.
故答案为2,该函数有最大值.
【点评】本题考查了函数的定义:对于函数概念的理解:①有两个变量;②一个变量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应.
25.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
【分析】(1)直接利用一次函数的定义分析得出答案;
(2)直接利用正比例函数的定义分析得出答案
【解答】解:(1)根据一次函数的定义,得:
2﹣|m|=1,
解得:m=±1.
又∵m+1≠0即m≠﹣1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:
2﹣|m|=1,n+4=0,
解得:m=±1,n=﹣4,
又∵m+1≠0即m≠﹣1,
∴当m=1,n=﹣4时,这个函数是正比例函数.
【点评】此题主要考查了一次函数以及正比例函数的定义,正确把握次数与系数的关系是解题关键.
26.已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
【分析】(1)根据描点法,可得函数图象;
(2)根据自变量与函数值的对应关系,可得答案;
(3)根据勾股定理,可得答案;
(4)根据三角形的面积公式,可得答案;
(5)根据一次还是的性质即可求得.
【解答】解:(1)如图:
;
(2)当y=0时,﹣2x﹣2=0,解得x=﹣1,即A(﹣1,0);
当x=0时,y=﹣2,即B(0,﹣2);
(3)由勾股定理得
AB==;
(4)S△AOB=×1×2=1;
(5)由一次函数y=﹣2x﹣2的系数k=﹣2<0可知:y随着x的增大而减小.
【点评】本题考查了一次函数图象和一次还是的性质,利用描点法画函数图象,利用自变量与函数值的对应关系求出相应的交点坐标.
27.有这样一个问题:探究函数y=的图象与性质.小美根据学习函数的经验,对函数y=的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)函数y=的自变量x的取值范围是 x≥﹣2且x≠0 ;
(2)下表是y与x的几组对应值.
x ﹣2 ﹣ ﹣1 ﹣ 1 2 3 4 …
y 0 ﹣ ﹣1 ﹣ m …
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质: 当﹣2≤x<0或x>0时,y随x增大而减小 .
【分析】(1)根据被开方数非负以及分母不为0即可得出关于x的一元一次不等式组,解之即可得出结论;
(2)将x=2代入函数解析式中求出m值即可;
(3)连点成线即可画出函数图象;
(4)观察函数图象,根据函数图象可寻找到函数具有单调性.
【解答】解:(1)由题意得:,
解得:x≥﹣2且x≠0.
故答案为:x≥﹣2且x≠0.
(2)当x=2时,m==1.
(3)图象如图所示.
(4)观察函数图象发现:当﹣2≤x<0或x>0时,y随x增大而减小.
故答案为:当﹣2≤x<0或x>0时,y随x增大而减小.
【点评】本题考查了函数自变量的取值范围以及函数图象,连点成曲线画出函数图象是解题的关键.
28.已知反比例函数y=,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
【分析】(1)把点A的坐标代入函数解析式,利用待定系数法求解即可;
(2)根据反比例函数图象的性质得到:k﹣1<0,由此求得k的取值范围;
(3)把点B、C的坐标代入函数解析式进行一一验证.
【解答】解:(1)∵点A(1,2)在这个函数的图象上,
∴k﹣1=1×2,
解得k=3;
(2)∵在函数y=图象的每一支上,y随x的增大而增大,
∴k﹣1<0,
解得k<1;
(3)∵k=13,有k﹣1=12,
∴反比例函数的解析式为y=.
将点B的坐标代入y=,可知点B的坐标满足函数关系式,
∴点B在函数y=的图象上,
将点C的坐标代入y=,由5≠,可知点C的坐标不满足函数关系式,
∴点C不在函数y=的图象上.
【点评】本题考查了反比例函数的性质,待定系数法求反比例函数解析式.注意:反比例函数的增减性只指在同一象限内.
一.选择题(共12小题)
1.已知y轴上的点P到原点的距离为5,则点P的坐标为( )
A.(5,0) B.(0,5)或(0,﹣5)
C.(0,5) D.(5,0)或(﹣5,0)
2.已知点P(m,1)在第二象限,则点Q(﹣m,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,若象棋盘上建立直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),那么“炮”位于点( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,2) D.(1,﹣2)
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
5.下列各图中反映了变量y是x的函数是( )
A. B.
C. D.
6.如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+1+n C.y=2n+n D.y=2n+n+1
7.要使函数y=(m﹣2)xn﹣1+n是一次函数,应满足( )
A.m≠2,n≠2 B.m=2,n=2 C.m≠2,n=2 D.m=2,n=0
8.下列函数中,y是x的正比例函数的是( )
A.y=2x﹣1 B.y= C.y=2x2 D.y=﹣2x+1
9.直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A. B.
C. D.
10.下列函数中,是反比例函数的为( )
A.y= B.y= C.y=2x+1 D.2y=x
11.若反比例函数的图象经过点A(,﹣2),则一次函数y=﹣kx+k与在同一坐标系中的大致图象是( )
A. B.
C. D.
12.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
二.填空题(共8小题)
13.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 .
14.如图,象棋盘上,若“将”位于点(0,0),“车”位于点(﹣4,0),则“马”位于 .
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 随 变化而变化,其中自变量是 ,因变量是 .
16.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ℃.
17.若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= .
18.若函数y=(k﹣1)x|k|是正比例函数,则k= .
19.将x=代入反比例函数y=﹣中,所得的函数值记为y1,又将x=y1+1代入反比例函数y=﹣中,所得的函数值记为y2,又将x=y2+1代入反比例函数y=﹣中,所得的函数值记为y3,…如此继续下去,则y2008= .
20.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 .
三.解答题(共8小题)
21.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
22.如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4).请根据图中所给信息解决下列问题:
(1)A→C( , );B→C( , );C→ (﹣3,﹣4);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出妮妮的位置E点.
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
24.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 ;
②该函数的一条性质: .
25.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
26.已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
27.有这样一个问题:探究函数y=的图象与性质.小美根据学习函数的经验,对函数y=的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x ﹣2 ﹣ ﹣1 ﹣ 1 2 3 4 …
y 0 ﹣ ﹣1 ﹣ m …
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质: .
28.已知反比例函数y=,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
2020年华师大新版数学下册八年级《第17章 函数及其图象》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.已知y轴上的点P到原点的距离为5,则点P的坐标为( )
A.(5,0) B.(0,5)或(0,﹣5)
C.(0,5) D.(5,0)或(﹣5,0)
【分析】首先根据点在y轴上,确定点P的横坐标为0,再根据P到原点的距离为5,确定P点的纵坐标,要注意分两情况考虑才不漏解,P可能在原点上方,也可能在原点下方.
【解答】解:由题中y轴上的点P得知:P点的横坐标为0;
∵点P到原点的距离为5,
∴点P的纵坐标为±5,
所以点P的坐标为(0,5)或(0,﹣5).
故选:B.
【点评】此题主要考查了由点到原点的距离确定点的坐标,要注意点在坐标轴上时,点到原点的距离要分两种情况考虑.
2.已知点P(m,1)在第二象限,则点Q(﹣m,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据第二象限内点的横坐标是负数判断出m<0,再根据各象限内点的坐标特征解答.
【解答】解:∵点P(m,1)在第二象限,
∴m<0,
∴﹣m>0,
∴点Q(﹣m,3)在第一象限.
故选:A.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
3.如图,若象棋盘上建立直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),那么“炮”位于点( )
A.(1,﹣1) B.(﹣1,1) C.(﹣1,2) D.(1,﹣2)
【分析】先利用“象”所在点的坐标画出直角坐标系,然后写出“炮”所在点的坐标即可.
【解答】解:如图,“炮”位于点(﹣1,1).
故选:B.
【点评】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.
4.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
【分析】根据自变量、因变量的含义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【解答】解:∵在这个变化中,自变量是温度,因变量是声速,
∴选项A正确;
∵根据数据表,可得温度越高,声速越快,
∴选项B正确;
∵342×5=1710(m),
∴当空气温度为20℃时,声音5s可以传播1710m,
∴选项C错误;
∵324﹣318=6(m/s),330﹣324=6(m/s),336﹣330=6(m/s),342﹣336=6(m/s),348﹣342=6(m/s),
∴当温度每升高10℃,声速增加6m/s,
∴选项D正确.
故选:C.
【点评】此题主要考查了自变量、因变量的含义和判断,要熟练掌握.
5.下列各图中反映了变量y是x的函数是( )
A. B.
C. D.
【分析】函数的意义反映在图象上简单的判断方法是:做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
【解答】解:根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,
只有D正确.
故选:D.
【点评】本题主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
6.如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+1+n C.y=2n+n D.y=2n+n+1
【分析】根据题意得:第1个图:y=1+2,第2个图:y=2+4=2+22,第3个图:y=3+8=3+23,…以此类推第n个图:y=n+2n,即可得到答案.
【解答】解:根据题意得:
第1个图:y=1+2,
第2个图:y=2+4=2+22,
第3个图:y=3+8=3+23,
…
以此类推
第n个图:y=n+2n,
故选:C.
【点评】本题考查了函数关系式和规律型:图形的变化类,正确找出规律,进行猜想归纳即可.
7.要使函数y=(m﹣2)xn﹣1+n是一次函数,应满足( )
A.m≠2,n≠2 B.m=2,n=2 C.m≠2,n=2 D.m=2,n=0
【分析】根据y=kx+b(k、b是常数,k≠0)是一次函数,可得m﹣2≠0,n﹣1=1,可得答案.
【解答】解:∵y=(m﹣2)xn﹣1+n是一次函数,
∴m﹣2≠0,n﹣1=1,
∴m≠2,n=2,
故选:C.
【点评】本题考查了一次函数,y=kx+b,k、b是常数,k≠0,x的次数等于1是解题关键.
8.下列函数中,y是x的正比例函数的是( )
A.y=2x﹣1 B.y= C.y=2x2 D.y=﹣2x+1
【分析】根据正比例函数的定义:一般地,两个变量x,y之间的关系式可以表示成形如y=kx(k为常数,且k≠0)的函数,那么y就叫做x的正比例函数.
【解答】解:根据正比例函数的定义可知选B.
故选:B.
【点评】主要考查正比例函数的定义:一般地,两个变量x,y之间的关系式可以表示成形如y=kx(k为常数,且k≠0)的函数,那么y就叫做x的正比例函数.
9.直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A. B.
C. D.
【分析】根据一次函数的系数与图象的关系依次分析选项,找k、b取值范围相同的即得答案.
【解答】解:根据一次函数的系数与图象的关系依次分析选项可得:
A、由图可得,y1=kx+b中,k<0,b<0,y2=bx+k中,b>0,k<0,b、k的取值矛盾,故本选项错误;
B、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b>0,k>0,b的取值相矛盾,故本选项错误;
C、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b<0,k>0,k的取值相一致,故本选项正确;
D、由图可得,y1=kx+b中,k>0,b<0,y2=bx+k中,b<0,k<0,k的取值相矛盾,故本选项错误;
故选:C.
【点评】本题主要考查了一次函数的图象性质,要掌握它们的性质才能灵活解题.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.
10.下列函数中,是反比例函数的为( )
A.y= B.y= C.y=2x+1 D.2y=x
【分析】根据反比例函数的定义回答即可.
【解答】解:A、是反比例函数,故A符合题意;
B、不是反比例函数,故B不符合题意;
C、是一次函数,故C不符合题意;
D、是正比例函数,故D不符合题意.
故选:A.
【点评】本题主要考查的是反比例函数的定义,掌握反比例函数的定义是解题的关键.
11.若反比例函数的图象经过点A(,﹣2),则一次函数y=﹣kx+k与在同一坐标系中的大致图象是( )
A. B.
C. D.
【分析】首先利用待定系数法算出反比例函数k的值,再根据k的值确定反比例函数所在象限,根据k的值确定一次函数解析式,根据一次函数解析式确定一次函数图象所在象限,即可选出答案.
【解答】解:∵反比例函数的图象经过点A(,﹣2),
∴k=×(﹣2)=﹣1,
∴反比例函数解析式为:y=﹣,
∴图象过第二、四象限,
∵k=﹣1,
∴一次函数y=x﹣1,
∴图象经过第一、三、四象限,
联立两函数解析式可得:﹣=x﹣1,
则x2﹣x+1=0,
∵△=1﹣4<0,
∴两函数图象无交点,
故选:D.
【点评】此题主要考查了待定系数法求反比例函数解析式,以及一次函数与反比例函数图象的性质,关键是根据k的值正确确定函数图象所在象限.
12.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
【分析】根据反比例函数的关于原点对称的性质知,正比例函数y=2x和反比例函数的另一个交点与点(1,2)关于原点对称.
【解答】解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
【点评】本题考查了反比例函数图象的对称性.关于原点对称的两点的横纵坐标互为相反数.
二.填空题(共8小题)
13.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 (﹣4,3) .
【分析】根据第二象限点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
【解答】解:∵点P在第二象限,且到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标为﹣4,纵坐标为3,
∴点P的坐标为(﹣4,3).
故答案为:(﹣4,3).
【点评】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.
14.如图,象棋盘上,若“将”位于点(0,0),“车”位于点(﹣4,0),则“马”位于 (3,3) .
【分析】根据已知两点的坐标建立坐标系,然后确定其它点的坐标.
【解答】解:结合图形以“将”(0,0)作为基准点,则“马”位于(0+3,0+3),
即(3,3).
故答案为:(3,3).
【点评】此题主要考查了点的坐标确定位置,解决此类问题需要先确定原点的位置,再求未知点的位置.或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 温度 随 时间 变化而变化,其中自变量是 时间 ,因变量是 温度 .
【分析】根据函数的定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应;来解答即可.
【解答】解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
【点评】函数的定义:设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数,记作y=f(x);变量是指在程序的运行过程中随时可以发生变化的量.
16.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ﹣40 ℃.
【分析】根据题意得x+32=x,解方程即可求得x的值.
【解答】解:根据题意得x+32=x,
解得x=﹣40.
故答案是:﹣40.
【点评】本题考查了函数的关系式,根据摄氏度数值与华氏度数值恰好相等转化为解方程问题是关键.
17.若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= ﹣3 .
【分析】根据一次函数的定义得到a=±3,且a≠3即可得到答案.
【解答】解:∵函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,
∴a=±3,
又∵a≠3,
∴a=﹣3.
故答案为:﹣3.
【点评】本题考查了一次函数的定义:对于y=kx+b(k、b为常数,k≠0),y称为x的一次函数.
18.若函数y=(k﹣1)x|k|是正比例函数,则k= ﹣1 .
【分析】根据正比例函数的定义,可得k﹣1≠0,|k|=1,从而求出k值.
【解答】解:∵根据正比例函数的定义,
可得:k﹣1≠0,|k|=1,
∴k=﹣1.
故答案为:﹣1.
【点评】考查了正比例函数的定义,解题关键是掌握正比例函数的定义条件,正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.
19.将x=代入反比例函数y=﹣中,所得的函数值记为y1,又将x=y1+1代入反比例函数y=﹣中,所得的函数值记为y2,又将x=y2+1代入反比例函数y=﹣中,所得的函数值记为y3,…如此继续下去,则y2008= ﹣ .
【分析】分别计算出y1,y2,y3,y4,可得到每三个一循环,而2008=669×3…1,即可得到y2008=y1,继而得出答案.
【解答】解:当x=时,y1=﹣;
当x=﹣+1=﹣时,y2=2,
当x=2+1=3时,y3=﹣,
当x=﹣+1=时,y4=﹣;
按照规律,y5=2,…,我们发现,y的值三个一循环20,8÷3=669…1,
∴y2008=y1=﹣.
故答案为:﹣.
【点评】本题考查了反比例函数的定义,按照题目的叙述计算一下y的值,从中观察得到规律,是解决本题的关键.
20.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 k1<k2<k3 .
【分析】本题考查反比例函数与的图象特点.
【解答】解:读图可知:三个反比例函数y=的图象在第二象限;故k1<0;y=,y=在第一象限;且y=的图象距原点较远,故有:k1<k2<k3;综合可得:k1<k2<k3.故填k1<k2<k3.
【点评】反比例函数y=的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.且图象距原点越远,k的绝对值越大.
三.解答题(共8小题)
21.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
【分析】(1)根据各点所在的象限,对应的横坐标、纵坐标,分别写出点的坐标;
(2)首先把四边形ABCD分割成规则图形,再求其面积和即可.
【解答】解:(1)A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
【点评】此题主要考查了点的坐标,以及求不规则图形的面积,关键是把不规则的图形正确的分割成规则图形.
22.如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4).请根据图中所给信息解决下列问题:
(1)A→C( +3 , +4 );B→C( +2 , 0 );C→ A (﹣3,﹣4);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出妮妮的位置E点.
【分析】(1)根据标记的第一个数字表示左、右方向,第二个数字表示上、下方向依次写出即可;
(2)根据运动路线列式计算即可得解;
(3)在图中依次表示出各位置,然后确定出点E的位置即可.
【解答】解:(1)A→C(+3,+4);B→C(+2,0);C→A (﹣3,﹣4);
故答案为:+3,+4;+2,0;A;
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
根据题意得:|+1|+|+4|+|+2|+|0|+|+1|+|﹣2|=10m.
(3)妮妮的位置E点如图所示.
【点评】本题考查了坐标确定位置,读懂题目信息,理解标记的两个数的实际意义是解题的关键.
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
【分析】根据总价=单价×数量,可得函数关系式.
【解答】解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
【点评】主要考查了常量与变量.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
24.已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x … 1 2 3 5 7 9 …
y … 1.98 3.95 2.63 1.58 1.13 0.88 …
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为 2 ;
②该函数的一条性质: 该函数有最大值 .
【分析】(1)按照自变量由小到大,利用平滑的曲线连结各点即可;
(2)①在所画的函数图象上找出自变量为4所对应的函数值即可;
②利用函数图象有最高点求解.
【解答】解:(1)如图,
(2)①x=4对应的函数值y约为2.0;
②该函数有最大值.
故答案为2,该函数有最大值.
【点评】本题考查了函数的定义:对于函数概念的理解:①有两个变量;②一个变量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应.
25.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
【分析】(1)直接利用一次函数的定义分析得出答案;
(2)直接利用正比例函数的定义分析得出答案
【解答】解:(1)根据一次函数的定义,得:
2﹣|m|=1,
解得:m=±1.
又∵m+1≠0即m≠﹣1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,得:
2﹣|m|=1,n+4=0,
解得:m=±1,n=﹣4,
又∵m+1≠0即m≠﹣1,
∴当m=1,n=﹣4时,这个函数是正比例函数.
【点评】此题主要考查了一次函数以及正比例函数的定义,正确把握次数与系数的关系是解题关键.
26.已知一次函数y=﹣2x﹣2.
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
【分析】(1)根据描点法,可得函数图象;
(2)根据自变量与函数值的对应关系,可得答案;
(3)根据勾股定理,可得答案;
(4)根据三角形的面积公式,可得答案;
(5)根据一次还是的性质即可求得.
【解答】解:(1)如图:
;
(2)当y=0时,﹣2x﹣2=0,解得x=﹣1,即A(﹣1,0);
当x=0时,y=﹣2,即B(0,﹣2);
(3)由勾股定理得
AB==;
(4)S△AOB=×1×2=1;
(5)由一次函数y=﹣2x﹣2的系数k=﹣2<0可知:y随着x的增大而减小.
【点评】本题考查了一次函数图象和一次还是的性质,利用描点法画函数图象,利用自变量与函数值的对应关系求出相应的交点坐标.
27.有这样一个问题:探究函数y=的图象与性质.小美根据学习函数的经验,对函数y=的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)函数y=的自变量x的取值范围是 x≥﹣2且x≠0 ;
(2)下表是y与x的几组对应值.
x ﹣2 ﹣ ﹣1 ﹣ 1 2 3 4 …
y 0 ﹣ ﹣1 ﹣ m …
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质: 当﹣2≤x<0或x>0时,y随x增大而减小 .
【分析】(1)根据被开方数非负以及分母不为0即可得出关于x的一元一次不等式组,解之即可得出结论;
(2)将x=2代入函数解析式中求出m值即可;
(3)连点成线即可画出函数图象;
(4)观察函数图象,根据函数图象可寻找到函数具有单调性.
【解答】解:(1)由题意得:,
解得:x≥﹣2且x≠0.
故答案为:x≥﹣2且x≠0.
(2)当x=2时,m==1.
(3)图象如图所示.
(4)观察函数图象发现:当﹣2≤x<0或x>0时,y随x增大而减小.
故答案为:当﹣2≤x<0或x>0时,y随x增大而减小.
【点评】本题考查了函数自变量的取值范围以及函数图象,连点成曲线画出函数图象是解题的关键.
28.已知反比例函数y=,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
【分析】(1)把点A的坐标代入函数解析式,利用待定系数法求解即可;
(2)根据反比例函数图象的性质得到:k﹣1<0,由此求得k的取值范围;
(3)把点B、C的坐标代入函数解析式进行一一验证.
【解答】解:(1)∵点A(1,2)在这个函数的图象上,
∴k﹣1=1×2,
解得k=3;
(2)∵在函数y=图象的每一支上,y随x的增大而增大,
∴k﹣1<0,
解得k<1;
(3)∵k=13,有k﹣1=12,
∴反比例函数的解析式为y=.
将点B的坐标代入y=,可知点B的坐标满足函数关系式,
∴点B在函数y=的图象上,
将点C的坐标代入y=,由5≠,可知点C的坐标不满足函数关系式,
∴点C不在函数y=的图象上.
【点评】本题考查了反比例函数的性质,待定系数法求反比例函数解析式.注意:反比例函数的增减性只指在同一象限内.
