人教版七年级下第五章5.3平行线的判定和性质的区别课件(30张PPT)
文档属性
| 名称 | 人教版七年级下第五章5.3平行线的判定和性质的区别课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 19:22:48 | ||
图片预览




文档简介
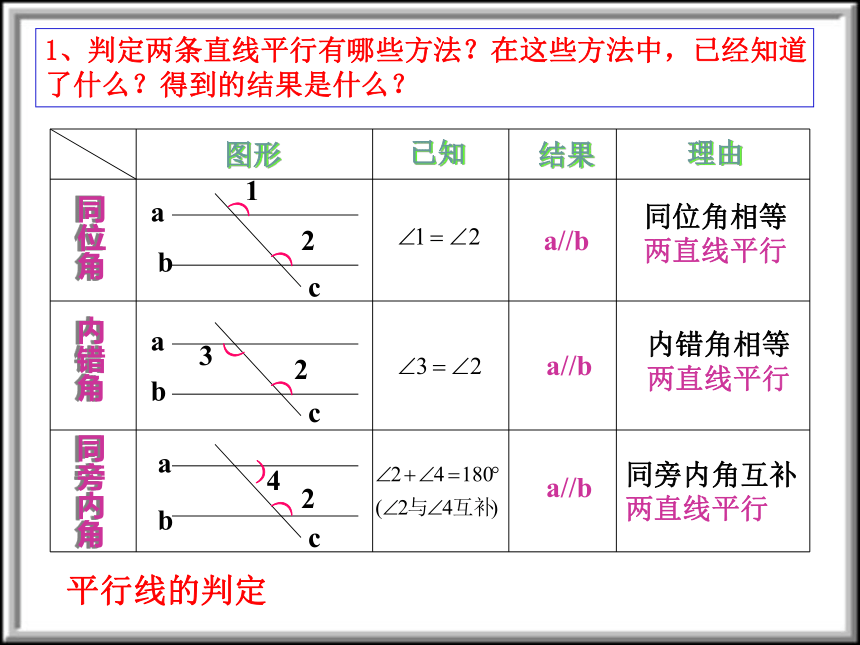
课件30张PPT。平行线的判定和性质的区别1、判定两条直线平行有哪些方法?在这些方法中,已经知道
了什么?得到的结果是什么?图形已知结果理由同位角内错角同旁内角a//ba//ba//b同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc平行线的判定图形已知结果理由同位角内错角同旁内角a//ba//b内错角相等
两直线平行同旁内角互补
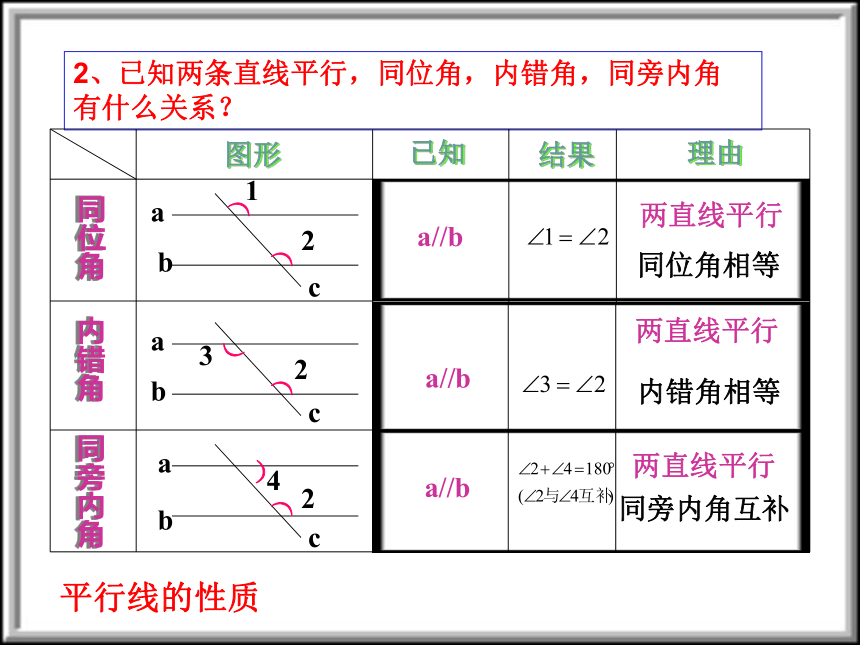
两直线平行122324))))))abababccc2、已知两条直线平行,同位角,内错角,同旁内角
有什么关系?a//b同位角相等
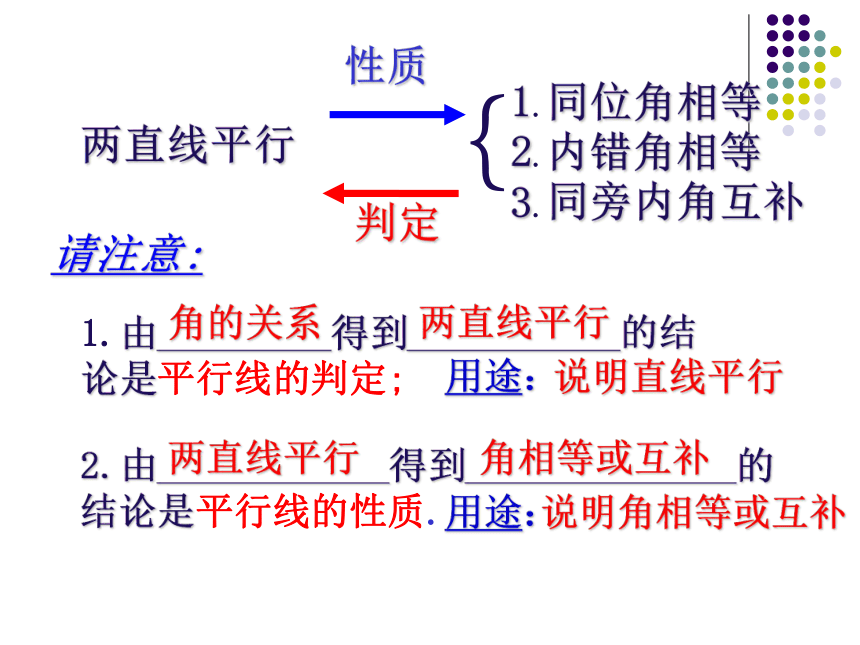
两直线平行a//b两直线平行同位角相等同旁内角互补a//b两直线平行平行线的性质∠2=∠3a//b两直线平行内错角相等两直线平行{1.同位角相等2.内错角相等3.同旁内角互补性质判定1.由_________得到___________的结论是平行线的判定;请注意:2.由____________得到______________的结论是平行线的性质.
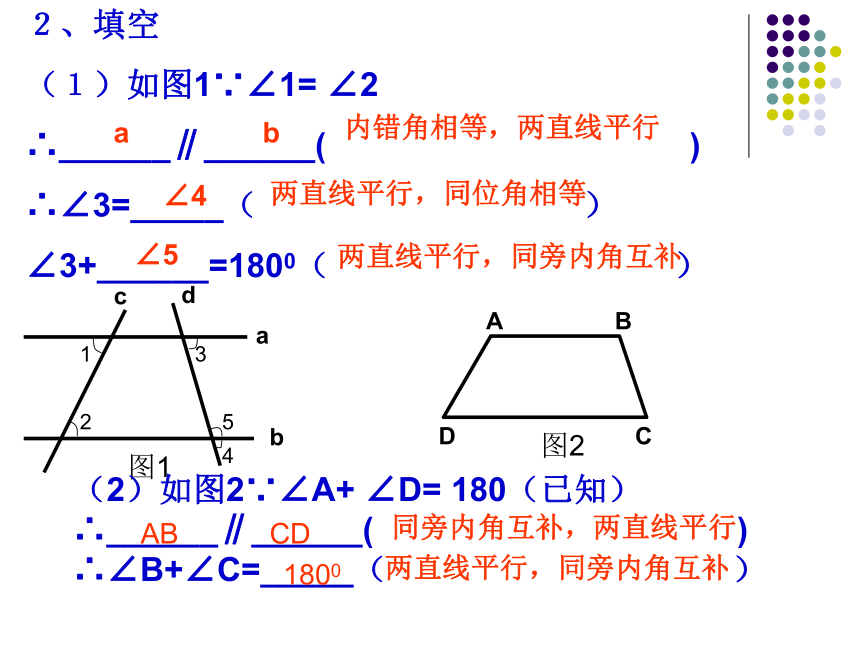
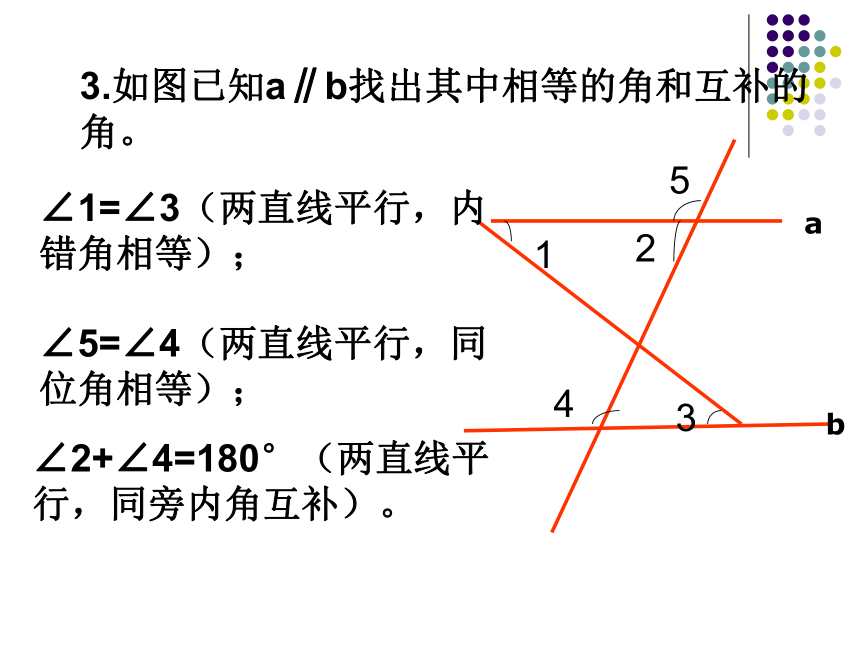
用途:用途:角的关系两直线平行说明直线平行两直线平行 角相等或互补说明角相等或互补DCDab内错角相等,两直线平行∠4两直线平行,同位角相等∠5两直线平行,同旁内角互补ABCD同旁内角互补,两直线平行1800两直线平行,同旁内角互补3.如图已知a∥b找出其中相等的角和互补的角。 12543∠1=∠3(两直线平行,内错角相等); ∠5=∠4(两直线平行,同位角相等);∠2+∠4=180°(两直线平行,同旁内角互补)。ab4.如图已知∠1=∠2,求证∠3+∠4=180°ABCD32541∴AB∥CD
(同位角相等,两直线平行)∴∠3=∠5( )∵∠4+∠5=180°( );∴∠3+∠4=180°(等量代换)证明:∵∠1=∠2
两直线平行,同位角相等邻补角的定义5、AP平分∠ BAC,CP平分∠ ACD, ∠1+ ∠2= 90°
判断直线AB、CD是否平行,说明理由。 12BAPCD变化题:如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.
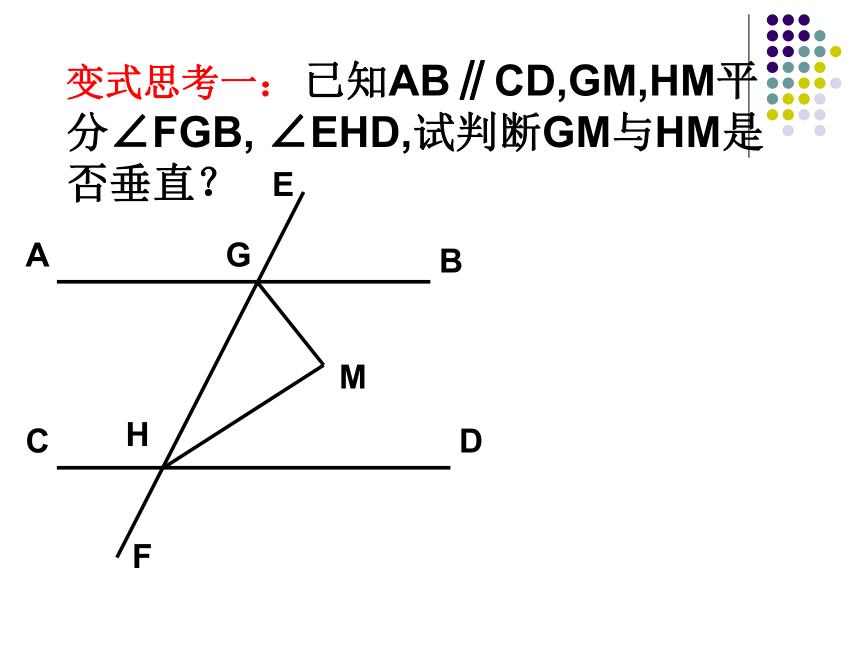
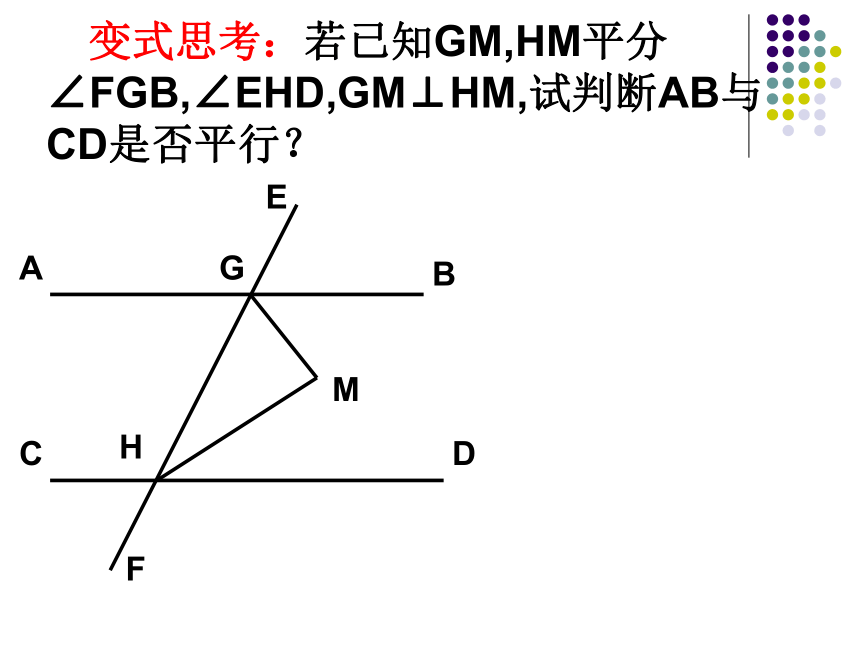
求证:∠1+∠2=90°.12ABCDE变式思考一: 已知AB∥CD,GM,HM平分∠FGB, ∠EHD,试判断GM与HM是否垂直? 变式思考:若已知GM,HM平分∠FGB,∠EHD,GM⊥HM,试判断AB与CD是否平行?6、如图,∠C=∠E+ ∠A,判断AB与CD是否平行,
并说明理由
F7、如图1,已知AD∥BC,∠BAD=∠BCD。判断AB与CD是否平行,并说明理由。8、如图2,已知AB∥CD,AE∥DF。请说明∠BAE=∠CDF9.有一条长方形纸带,按如图所示沿AB折叠时,当∠1=30°求纸带重叠部分中∠CAB的度数。 ∠CAB =75°回顾与思考 如图,已知AB∥CD,求证:∠AEC=∠C+∠A 。自己动手做回顾与思考 如图,已知∠AEC=∠C+∠A,求证:AB∥CD自己动手做问题2:如图,已知:AB∥CD
求证: ∠C=∠A+∠PADPCBMN问题3: AB∥CD,分别探讨下面四个图形中∠A、∠C、∠P 满足的关系式:(1)(4)(3)(2)问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.方法1方法2方法3⌒ABCDE⌒110°150°40°答: ∠C= 140°∵AD∥BF(已知), ∠A=110°理由:过B作BF∥AD∴ ∠ABF= ∠A=110°∵AD ∥CE∵ ∠ABC=150°∴ ∠FBC= ∠ABC— ∠ABF =40°∴CE ∥BF(平行于同一条直线的两条直线互相平行)∴ ∠FBC+ ∠C=180°∴ ∠C=140°(两直线平行,同旁内角互补)(两直线平行,内错角相等)问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.D⌒ABCE⌒110°150°110°30°40°140°问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.D⌒ABCE⌒110°150°30 °140°添加辅助线的方法:①添加平行线②构造三角形连结线段作延长线问题2:如图,已知:AB∥CD
求证: ∠C=∠A+∠PADPCBMN问题3: AB∥CD,分别探讨下面四个图形中∠A、∠C、∠P 满足的关系式:(1)(4)(3)(2)回顾与思考 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.自己动手做回顾与思考 分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.回顾与思考 例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.学以致用 2、台球运动中,如果母球P击中桌边点A,经桌边反弹后
击中相邻的另一条桌边,再次反弹,
那么母球P经过的路线BC与PA平行吗?
请说明你判断的理由
了什么?得到的结果是什么?图形已知结果理由同位角内错角同旁内角a//ba//ba//b同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc平行线的判定图形已知结果理由同位角内错角同旁内角a//ba//b内错角相等
两直线平行同旁内角互补
两直线平行122324))))))abababccc2、已知两条直线平行,同位角,内错角,同旁内角
有什么关系?a//b同位角相等
两直线平行a//b两直线平行同位角相等同旁内角互补a//b两直线平行平行线的性质∠2=∠3a//b两直线平行内错角相等两直线平行{1.同位角相等2.内错角相等3.同旁内角互补性质判定1.由_________得到___________的结论是平行线的判定;请注意:2.由____________得到______________的结论是平行线的性质.
用途:用途:角的关系两直线平行说明直线平行两直线平行 角相等或互补说明角相等或互补DCDab内错角相等,两直线平行∠4两直线平行,同位角相等∠5两直线平行,同旁内角互补ABCD同旁内角互补,两直线平行1800两直线平行,同旁内角互补3.如图已知a∥b找出其中相等的角和互补的角。 12543∠1=∠3(两直线平行,内错角相等); ∠5=∠4(两直线平行,同位角相等);∠2+∠4=180°(两直线平行,同旁内角互补)。ab4.如图已知∠1=∠2,求证∠3+∠4=180°ABCD32541∴AB∥CD
(同位角相等,两直线平行)∴∠3=∠5( )∵∠4+∠5=180°( );∴∠3+∠4=180°(等量代换)证明:∵∠1=∠2
两直线平行,同位角相等邻补角的定义5、AP平分∠ BAC,CP平分∠ ACD, ∠1+ ∠2= 90°
判断直线AB、CD是否平行,说明理由。 12BAPCD变化题:如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.
求证:∠1+∠2=90°.12ABCDE变式思考一: 已知AB∥CD,GM,HM平分∠FGB, ∠EHD,试判断GM与HM是否垂直? 变式思考:若已知GM,HM平分∠FGB,∠EHD,GM⊥HM,试判断AB与CD是否平行?6、如图,∠C=∠E+ ∠A,判断AB与CD是否平行,
并说明理由
F7、如图1,已知AD∥BC,∠BAD=∠BCD。判断AB与CD是否平行,并说明理由。8、如图2,已知AB∥CD,AE∥DF。请说明∠BAE=∠CDF9.有一条长方形纸带,按如图所示沿AB折叠时,当∠1=30°求纸带重叠部分中∠CAB的度数。 ∠CAB =75°回顾与思考 如图,已知AB∥CD,求证:∠AEC=∠C+∠A 。自己动手做回顾与思考 如图,已知∠AEC=∠C+∠A,求证:AB∥CD自己动手做问题2:如图,已知:AB∥CD
求证: ∠C=∠A+∠PADPCBMN问题3: AB∥CD,分别探讨下面四个图形中∠A、∠C、∠P 满足的关系式:(1)(4)(3)(2)问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.方法1方法2方法3⌒ABCDE⌒110°150°40°答: ∠C= 140°∵AD∥BF(已知), ∠A=110°理由:过B作BF∥AD∴ ∠ABF= ∠A=110°∵AD ∥CE∵ ∠ABC=150°∴ ∠FBC= ∠ABC— ∠ABF =40°∴CE ∥BF(平行于同一条直线的两条直线互相平行)∴ ∠FBC+ ∠C=180°∴ ∠C=140°(两直线平行,同旁内角互补)(两直线平行,内错角相等)问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.D⌒ABCE⌒110°150°110°30°40°140°问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.问题1:一条公路修到湖边时,需拐弯绕湖而行,如果第一 次拐角∠A是110°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度,请说明理由.D⌒ABCE⌒110°150°30 °140°添加辅助线的方法:①添加平行线②构造三角形连结线段作延长线问题2:如图,已知:AB∥CD
求证: ∠C=∠A+∠PADPCBMN问题3: AB∥CD,分别探讨下面四个图形中∠A、∠C、∠P 满足的关系式:(1)(4)(3)(2)回顾与思考 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.自己动手做回顾与思考 分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.回顾与思考 例2 如图,已知∠AEC=∠C+∠A,判断AB与∥CD是否平行?并说明理由.学以致用 2、台球运动中,如果母球P击中桌边点A,经桌边反弹后
击中相邻的另一条桌边,再次反弹,
那么母球P经过的路线BC与PA平行吗?
请说明你判断的理由
