人教版七年级下册第五章5.2.2平行线的判定课件(24张PPT)
文档属性
| 名称 | 人教版七年级下册第五章5.2.2平行线的判定课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1011.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 00:00:00 | ||
图片预览






文档简介
课件24张PPT。5.2.2 平行线的判定知识回顾:
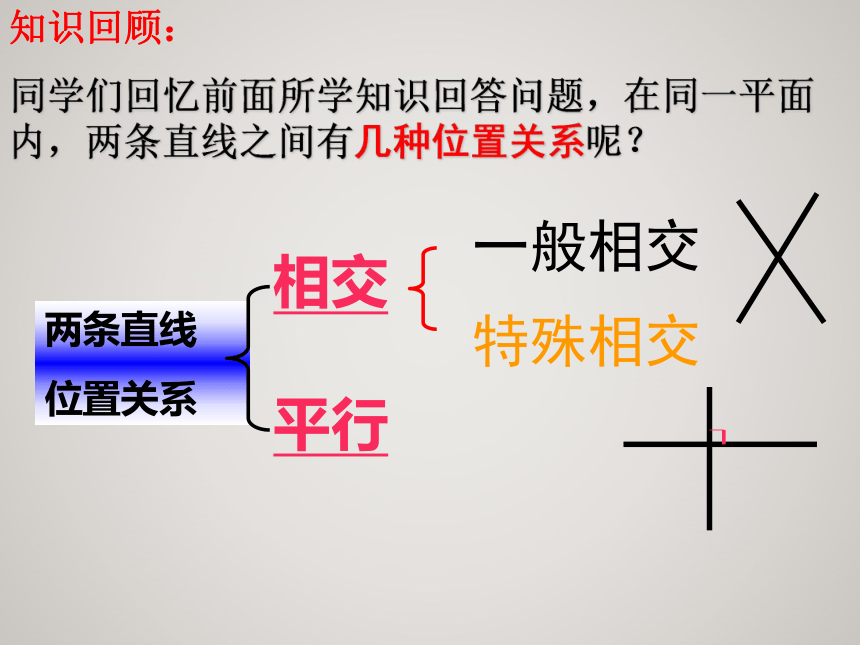
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢? 一般相交特殊相交两条直线
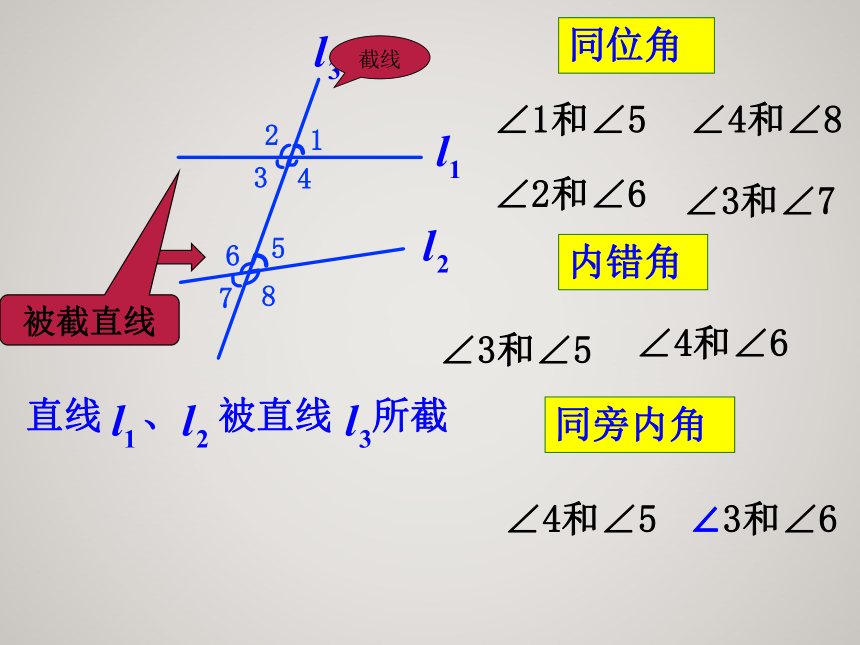
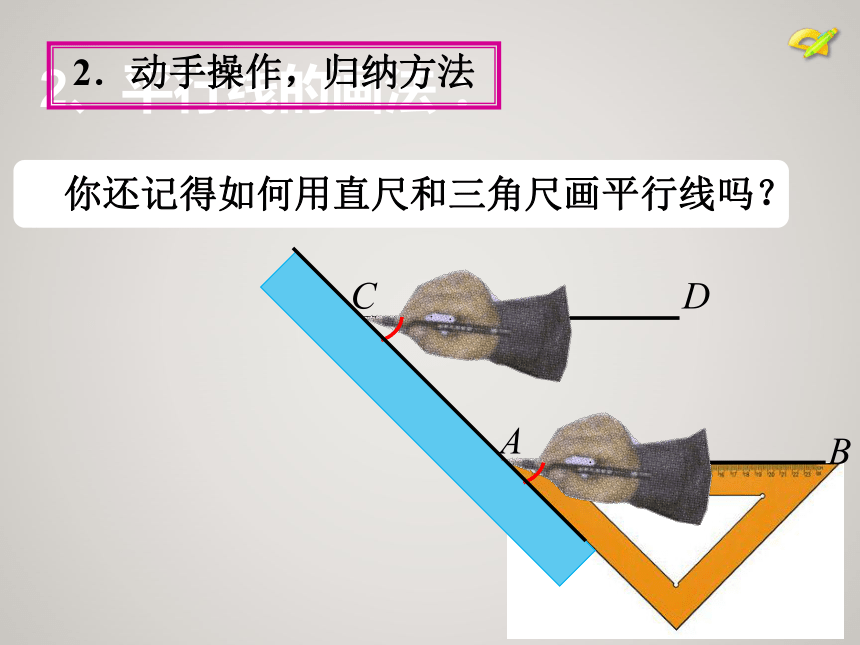
位置关系基本事实:经过直线外一点,有且只有一条直线与这条直线平行.基本事实推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.如果b∥a,c∥a,那么b∥c. 直线 、 被直线 所截同位角内错角同旁内角∠1和∠5∠4和∠8∠2和∠6∠3和∠7∠3和∠5∠4和∠6∠4和∠5∠3和∠6截线2、平行线的画法:2. 动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:·ABCD2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?∴AB∥CD.画图并回答问题:过直线l 外一点P画直线l 的平行线,
① 三角尺紧靠直尺的边和直线l 所成的角在平移前
的位置和平移后的位置构成了一对______角,
其大小______。
② 只要保持_________相等,画出的直线就平行于
已知直线。
③由上面的画图与问题,你能否用一句话来概括?同位始终不变同位角平行线的判定1. 两条直线被第三条直线所截,如果
同位角相等,那么两直线平行。简
单地说:同位角相等,两直线平行。 ∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)如图:如图,∠1=100°,∠2=100°,a∥b吗? 若∠2=100°,∠3=___时,a∥b。 不平行!80°练习:如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠1 =∠2∠2 =∠5∠3 =∠4∠3=∠4AB∥CDEF∥GHEF∥GH∠1=∠4想一想 “在同一平面 ,垂直于同一条直线的两条直线互相平行”是否可以看做平行线判定方法的特殊情形?∵∠1=∠3=90°∥大家来探索!① 如图: 如果∠1=∠2,
那么a与b平行吗?② 如图: 如果∠1+∠2=180o,
那么a与b平行吗?内错角相等,两直线平行。∵ ____=____(已知)
∴ ___∥___(内错角相等,两直线平行)
① 如图: 如果∠1=∠2,
那么a与b平行吗?∠1∠2ab∵ ____+____=180o(已知)
∴ ___∥___(同旁内角互补,两直线平行)② 如图: 如果∠1+∠2=180o,
那么a与b平行吗?同旁内角互补,两直线平行。∠1∠2ab进一步探索!1.两条直线被第三条直线所截,如果同位角等,那么两直线平行。简单地说:同位角相等,两直线平行。2. 两条直线被第三条直线所截,如果内错角相等,那么两直线平行。简单地说:内错角相等,两直线平行。3. 两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。简单地说:同旁内角互补,两直线平行。例题讲解例1:如图,∠A= 55 °,∠B=125 °,AD与BC平行吗?AB与CD平行吗?为什么?[ 根据题目中现有的条件,无法判断AB与CD平行。]解:
∵∠A +∠B = 55 °+ 125 °= 180° ∴AD//BC(同旁内角互补,两直线平行)解:∵∠1= 70 °,例2 、如图∠1=70 °,∠2=110 °,试判断AD//BC 吗?并说明理由。 ∴∠3=110 °( 邻补角的定义)∴∠2 =∠3=110 °∴ AD//BC (内错角相等,两直线平行)例题讲解还有其他的证明方法吗???abcmn1234a ∥ b.c ∥m.c ∥n.1.当图中各角满足下列条件时,你能指出哪两条直线平行?
(1) ∠1 = ∠4,(2) ∠2 = ∠4,(3)∠1+ ∠3=180°,2.如图,
如果∠B=∠1,则可得 // ,
根据是 .
如果∠D=∠1,则可得到 // ,
根据是 . 同位角相等,两直线平行内错角相等,两直线平行3.如图,直线a,b被c所截,已知∠1=120°,∠2=60°,直线a,b平行吗?为什么? 解:a与b平行,
∵∠1=∠3(对顶角相等)
∠1=120°(已知)
∴∠3=120°
∵∠2=60°∴∠2+3=180°
∴a//b(同旁内角互补,
两直线平行) 1.如果∠A=∠3,那么 ∥ ,
( )
2.如果∠2=∠E,那么 ∥ ,
( )
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
4.如果∠2= ,那么DA∥EB
( )
5.如果∠DBC+ =1800,那么DB∥EC
( )ABCDE123AD BE同位角相等,两直线平行.BD CE内错角相等,两直线平行.AD BE同旁内角互补,两直线平行.∠D内错角相等,两直线平行.∠C同旁内角互补,两直线平行.反馈评价
游戏接龙① ∵ ∠2 =___(已知)
∴ ___∥___② ∵ ∠3 = ∠5(已知)
∴ ___∥___③∵ ∠4 +___=180o(已知)
∴ ___∥___∠6ABCDABCD∠5ABCD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行① ∵ ∠1 =_____(已知)
∴ AB∥CE② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB∠3∠33.如图:内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢? 一般相交特殊相交两条直线
位置关系基本事实:经过直线外一点,有且只有一条直线与这条直线平行.基本事实推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.如果b∥a,c∥a,那么b∥c. 直线 、 被直线 所截同位角内错角同旁内角∠1和∠5∠4和∠8∠2和∠6∠3和∠7∠3和∠5∠4和∠6∠4和∠5∠3和∠6截线2、平行线的画法:2. 动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:·ABCD2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?∴AB∥CD.画图并回答问题:过直线l 外一点P画直线l 的平行线,
① 三角尺紧靠直尺的边和直线l 所成的角在平移前
的位置和平移后的位置构成了一对______角,
其大小______。
② 只要保持_________相等,画出的直线就平行于
已知直线。
③由上面的画图与问题,你能否用一句话来概括?同位始终不变同位角平行线的判定1. 两条直线被第三条直线所截,如果
同位角相等,那么两直线平行。简
单地说:同位角相等,两直线平行。 ∵ ∠1=∠2(已知)∴ a∥b(同位角相等,两直线平行)如图:如图,∠1=100°,∠2=100°,a∥b吗? 若∠2=100°,∠3=___时,a∥b。 不平行!80°练习:如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠1 =∠2∠2 =∠5∠3 =∠4∠3=∠4AB∥CDEF∥GHEF∥GH∠1=∠4想一想 “在同一平面 ,垂直于同一条直线的两条直线互相平行”是否可以看做平行线判定方法的特殊情形?∵∠1=∠3=90°∥大家来探索!① 如图: 如果∠1=∠2,
那么a与b平行吗?② 如图: 如果∠1+∠2=180o,
那么a与b平行吗?内错角相等,两直线平行。∵ ____=____(已知)
∴ ___∥___(内错角相等,两直线平行)
① 如图: 如果∠1=∠2,
那么a与b平行吗?∠1∠2ab∵ ____+____=180o(已知)
∴ ___∥___(同旁内角互补,两直线平行)② 如图: 如果∠1+∠2=180o,
那么a与b平行吗?同旁内角互补,两直线平行。∠1∠2ab进一步探索!1.两条直线被第三条直线所截,如果同位角等,那么两直线平行。简单地说:同位角相等,两直线平行。2. 两条直线被第三条直线所截,如果内错角相等,那么两直线平行。简单地说:内错角相等,两直线平行。3. 两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。简单地说:同旁内角互补,两直线平行。例题讲解例1:如图,∠A= 55 °,∠B=125 °,AD与BC平行吗?AB与CD平行吗?为什么?[ 根据题目中现有的条件,无法判断AB与CD平行。]解:
∵∠A +∠B = 55 °+ 125 °= 180° ∴AD//BC(同旁内角互补,两直线平行)解:∵∠1= 70 °,例2 、如图∠1=70 °,∠2=110 °,试判断AD//BC 吗?并说明理由。 ∴∠3=110 °( 邻补角的定义)∴∠2 =∠3=110 °∴ AD//BC (内错角相等,两直线平行)例题讲解还有其他的证明方法吗???abcmn1234a ∥ b.c ∥m.c ∥n.1.当图中各角满足下列条件时,你能指出哪两条直线平行?
(1) ∠1 = ∠4,(2) ∠2 = ∠4,(3)∠1+ ∠3=180°,2.如图,
如果∠B=∠1,则可得 // ,
根据是 .
如果∠D=∠1,则可得到 // ,
根据是 . 同位角相等,两直线平行内错角相等,两直线平行3.如图,直线a,b被c所截,已知∠1=120°,∠2=60°,直线a,b平行吗?为什么? 解:a与b平行,
∵∠1=∠3(对顶角相等)
∠1=120°(已知)
∴∠3=120°
∵∠2=60°∴∠2+3=180°
∴a//b(同旁内角互补,
两直线平行) 1.如果∠A=∠3,那么 ∥ ,
( )
2.如果∠2=∠E,那么 ∥ ,
( )
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
4.如果∠2= ,那么DA∥EB
( )
5.如果∠DBC+ =1800,那么DB∥EC
( )ABCDE123AD BE同位角相等,两直线平行.BD CE内错角相等,两直线平行.AD BE同旁内角互补,两直线平行.∠D内错角相等,两直线平行.∠C同旁内角互补,两直线平行.反馈评价
游戏接龙① ∵ ∠2 =___(已知)
∴ ___∥___② ∵ ∠3 = ∠5(已知)
∴ ___∥___③∵ ∠4 +___=180o(已知)
∴ ___∥___∠6ABCDABCD∠5ABCD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行① ∵ ∠1 =_____(已知)
∴ AB∥CE② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB∠3∠33.如图:内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行
