人教版七年级下第五章5.2.2平行线的判定(2)习题课课件(19张PPT)
文档属性
| 名称 | 人教版七年级下第五章5.2.2平行线的判定(2)习题课课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 00:00:00 | ||
图片预览




文档简介
课件19张PPT。习题课5.2.2平行线的判定
(2)知识回顾:两条直线平行的判定方法
方法1:如图1,若∠1=∠3,则a∥c
( )
方法2:如图1,若∠2=∠3,则a∥c
( )
方法3:如图1,若∠3+∠4=180°,则a∥c
( )同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行a
bc)))1234方法4:若a∥b,b∥c,则a∥c
( )
平行于同一条直线的两条直线平行 复习提问
1.如下图所示,请说出能够得到直线AB∥CD的所有直接条件,并说明理由。
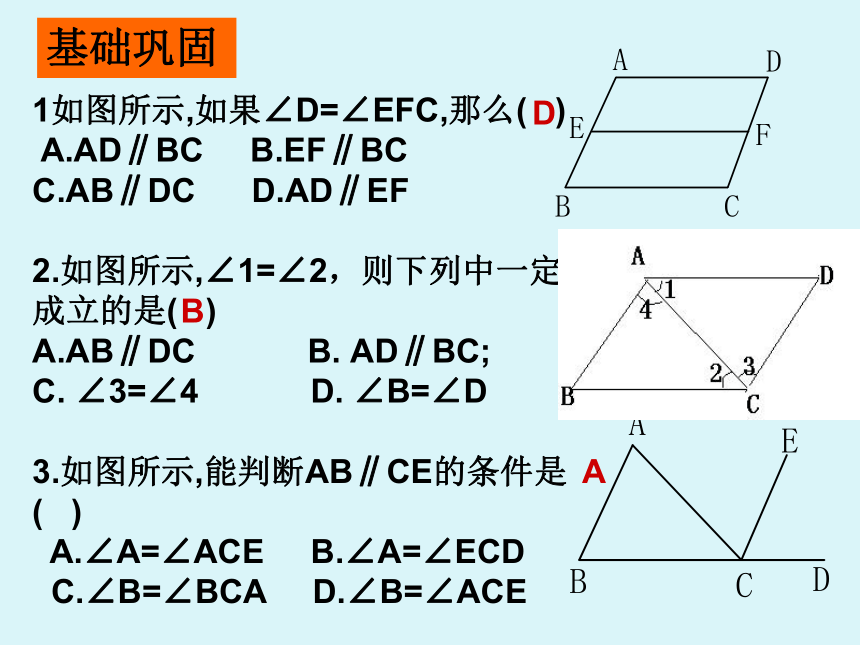
基础巩固1如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
2.如图所示,∠1=∠2,则下列中一定成立的是( )
A.AB∥DC B. AD∥BC;
C. ∠3=∠4 D. ∠B=∠D
3.如图所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD
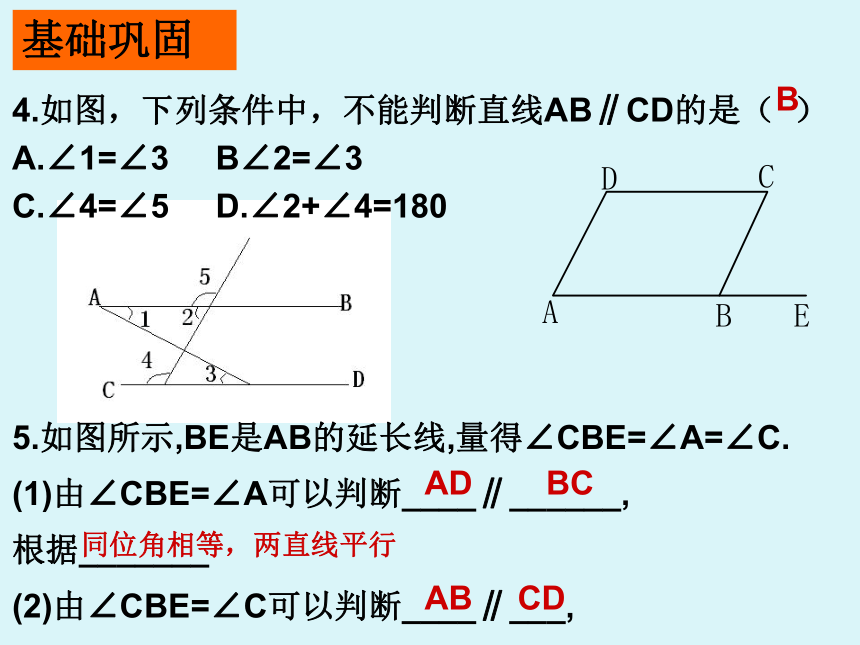
C.∠B=∠BCA D.∠B=∠ACEDBA4.如图,下列条件中,不能判断直线AB∥CD的是( )
A.∠1=∠3 B∠2=∠3
C.∠4=∠5 D.∠2+∠4=180
5.如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断____∥______,
根据_______
(2)由∠CBE=∠C可以判断____∥___,
根据是_________.
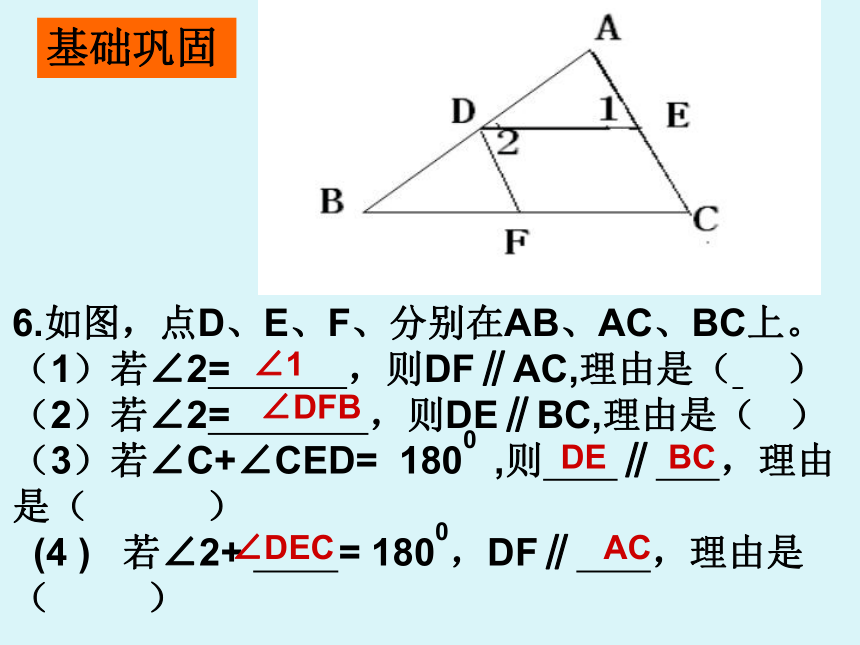
基础巩固BABCDADBC同位角相等,两直线平行内错角相等,两直线平行基础巩固6.如图,点D、E、F、分别在AB、AC、BC上。
(1)若∠2= ,则DF∥AC,理由是( )
(2)若∠2= ,则DE∥BC,理由是( )
(3)若∠C+∠CED= 1800 ,则 ∥ ,理由是( )
(4 ) 若∠2+ = 1800,DF∥ ,理由是( ) ∠1∠DFBDEBC∠DECAC例1.如图所示,直线AB、CD被直线EF所截,∠1=∠2,∠CNF=∠BME,那么AB∥CD,MP∥NQ,请给出证明。12证明:过P点作射线PE使∠1=∠A例2、如图,已知: ∠APC=∠A+∠C ,试探究AB与CD的位置关系,并证明你所探究的结论的正确性。例3: 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) FEMNA21BC证明:练习:
1.如图,
1) ∵∠1=∠2,
∴ ∥ .
( )
2) ∵ = ,(或 = )
∴ AB∥DC
( )
(或 )ABCD12EADBC内错角相等,两直线平行∠B∠DCE∠BAC∠ACD同位角相等,两直线平行内错角相等,两直线平行2、 如下图,已知∠1=120°, ∠C=60°
判断直线AB与CD是否平行ABCD)1)2答: AB∥CD理由:∵ ∠1=120°( )已知 ∴ ∠2=180°—∠1 =60° ( )
邻补角定义又∵ ∠C=60°( )已知 ∴ ∠2= ∠C( )
等量代换∴AB∥CD( )
同位角相等,两直线平行3.已知∠1=∠3,∠2与∠3互补,那么可以判断哪几组直线互相平行?答:有两组平行线,分别是AB?CD,BC? EFABBC4、如图,直线EF与∠ABC的一边BA,相交于D, ∠B+ ∠ADE=180°,EF与BC平行吗?为什么?ABEFDC答: EF与BC平行
理由:∵ ∠B+ ∠ADE=180( )已知∠ADE= ∠BDF( )
对顶角相等∴ ∠BDF+ ∠B=180°( )等量代换∴ EF∥BC( )
同旁内角互补,两直线平行5、如图, ∠B=∠C ∠B+∠D=180°,
那么BC平行DE吗?为什么?ABCDE答:BC∥DE
理由:∵ ∠B=∠C ( )已知∠B+ ∠D=180°( )
已知∴ ∠C+ ∠D=180°( )
等量代换∴BC∥DE( )
同旁内角互补,两直线平行6、已知直线AB、BC、CD、DA相交于点A、B、C、D,∠1=∠2 ,∠2+∠3=1800
求证:(1)AD∥BC
(2)AB∥CD7、如图,已知直线 , 被直线AB所截,AC 于点C.若 则 与 平行吗? 请说明理由.2.如图,已知直线 , 被直线 所截,
判断 与 是否平行 , 并说明理由. 拓展训练8、如图,直线AB过点C , ∠2=800, ∠D=500,∠1=∠3,AB∥DE吗?为什么?
判定两条直线是否平行的方法有:1.平行线的定义.2.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
3 .平行线的判定:(1).同位角相等, 两直线平行.
(2).内错角相等, 两直线平行.(3).同旁内角互补, 两直线平行.归纳小结
(2)知识回顾:两条直线平行的判定方法
方法1:如图1,若∠1=∠3,则a∥c
( )
方法2:如图1,若∠2=∠3,则a∥c
( )
方法3:如图1,若∠3+∠4=180°,则a∥c
( )同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行a
bc)))1234方法4:若a∥b,b∥c,则a∥c
( )
平行于同一条直线的两条直线平行 复习提问
1.如下图所示,请说出能够得到直线AB∥CD的所有直接条件,并说明理由。
基础巩固1如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
2.如图所示,∠1=∠2,则下列中一定成立的是( )
A.AB∥DC B. AD∥BC;
C. ∠3=∠4 D. ∠B=∠D
3.如图所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD
C.∠B=∠BCA D.∠B=∠ACEDBA4.如图,下列条件中,不能判断直线AB∥CD的是( )
A.∠1=∠3 B∠2=∠3
C.∠4=∠5 D.∠2+∠4=180
5.如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断____∥______,
根据_______
(2)由∠CBE=∠C可以判断____∥___,
根据是_________.
基础巩固BABCDADBC同位角相等,两直线平行内错角相等,两直线平行基础巩固6.如图,点D、E、F、分别在AB、AC、BC上。
(1)若∠2= ,则DF∥AC,理由是( )
(2)若∠2= ,则DE∥BC,理由是( )
(3)若∠C+∠CED= 1800 ,则 ∥ ,理由是( )
(4 ) 若∠2+ = 1800,DF∥ ,理由是( ) ∠1∠DFBDEBC∠DECAC例1.如图所示,直线AB、CD被直线EF所截,∠1=∠2,∠CNF=∠BME,那么AB∥CD,MP∥NQ,请给出证明。12证明:过P点作射线PE使∠1=∠A例2、如图,已知: ∠APC=∠A+∠C ,试探究AB与CD的位置关系,并证明你所探究的结论的正确性。例3: 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) FEMNA21BC证明:练习:
1.如图,
1) ∵∠1=∠2,
∴ ∥ .
( )
2) ∵ = ,(或 = )
∴ AB∥DC
( )
(或 )ABCD12EADBC内错角相等,两直线平行∠B∠DCE∠BAC∠ACD同位角相等,两直线平行内错角相等,两直线平行2、 如下图,已知∠1=120°, ∠C=60°
判断直线AB与CD是否平行ABCD)1)2答: AB∥CD理由:∵ ∠1=120°( )已知 ∴ ∠2=180°—∠1 =60° ( )
邻补角定义又∵ ∠C=60°( )已知 ∴ ∠2= ∠C( )
等量代换∴AB∥CD( )
同位角相等,两直线平行3.已知∠1=∠3,∠2与∠3互补,那么可以判断哪几组直线互相平行?答:有两组平行线,分别是AB?CD,BC? EFABBC4、如图,直线EF与∠ABC的一边BA,相交于D, ∠B+ ∠ADE=180°,EF与BC平行吗?为什么?ABEFDC答: EF与BC平行
理由:∵ ∠B+ ∠ADE=180( )已知∠ADE= ∠BDF( )
对顶角相等∴ ∠BDF+ ∠B=180°( )等量代换∴ EF∥BC( )
同旁内角互补,两直线平行5、如图, ∠B=∠C ∠B+∠D=180°,
那么BC平行DE吗?为什么?ABCDE答:BC∥DE
理由:∵ ∠B=∠C ( )已知∠B+ ∠D=180°( )
已知∴ ∠C+ ∠D=180°( )
等量代换∴BC∥DE( )
同旁内角互补,两直线平行6、已知直线AB、BC、CD、DA相交于点A、B、C、D,∠1=∠2 ,∠2+∠3=1800
求证:(1)AD∥BC
(2)AB∥CD7、如图,已知直线 , 被直线AB所截,AC 于点C.若 则 与 平行吗? 请说明理由.2.如图,已知直线 , 被直线 所截,
判断 与 是否平行 , 并说明理由. 拓展训练8、如图,直线AB过点C , ∠2=800, ∠D=500,∠1=∠3,AB∥DE吗?为什么?
判定两条直线是否平行的方法有:1.平行线的定义.2.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
3 .平行线的判定:(1).同位角相等, 两直线平行.
(2).内错角相等, 两直线平行.(3).同旁内角互补, 两直线平行.归纳小结
