人教版七年级下第五章5.2.2平行线的判定(2)课件(22张PPT)
文档属性
| 名称 | 人教版七年级下第五章5.2.2平行线的判定(2)课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 193.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 00:00:00 | ||
图片预览





文档简介
课件22张PPT。平行线的判定Ⅱ
学习目标
1、理解平行线的三种判定方法,会结合图形用符号语言表示“平行线的判定”的书写格式;
2、经历由“平行线的判定方法一”推导出“平行线的判定方法二、三”的过程,初步体验“简单推理”过程,体会数学中的转化思想;
3、会运用“平行线的判定方法”来判定两条直线是否平行,学会简单的说理。
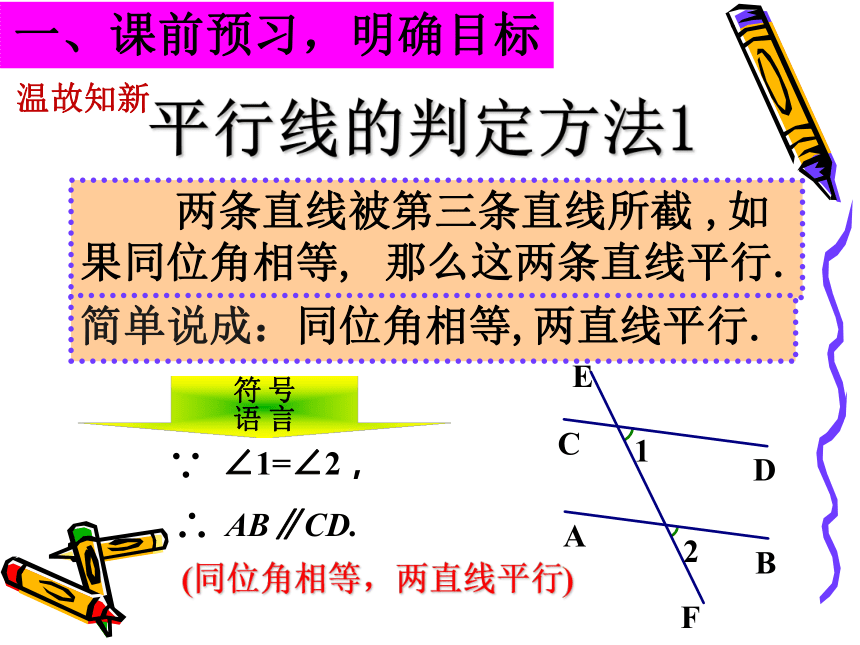
几何画板.gsp温故知新 两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.平行线的判定方法1简单说成:同位角相等,两直线平行.号言
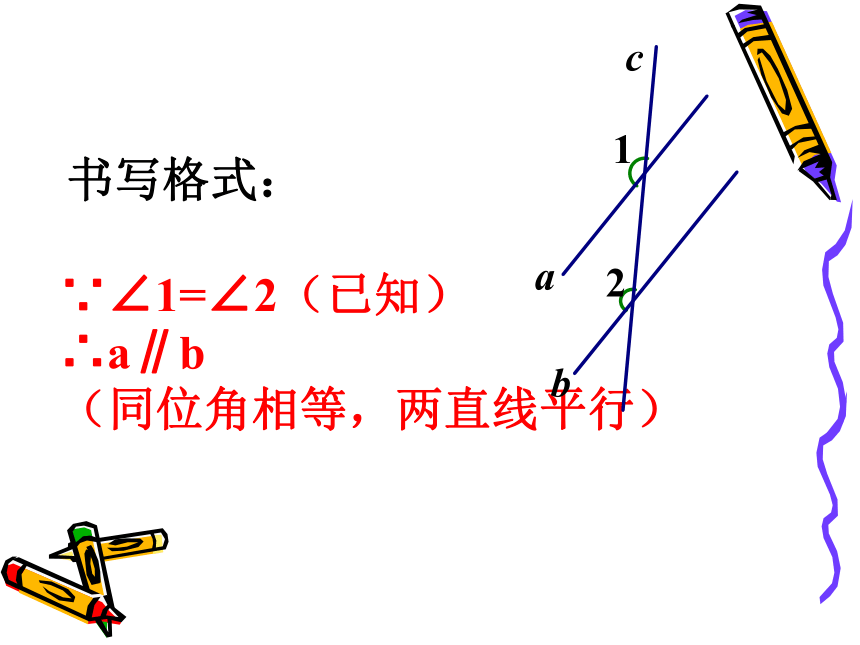
符语(同位角相等,两直线平行)一、课前预习,明确目标温故知新∵∠1=∠2(已知)
∴a∥b
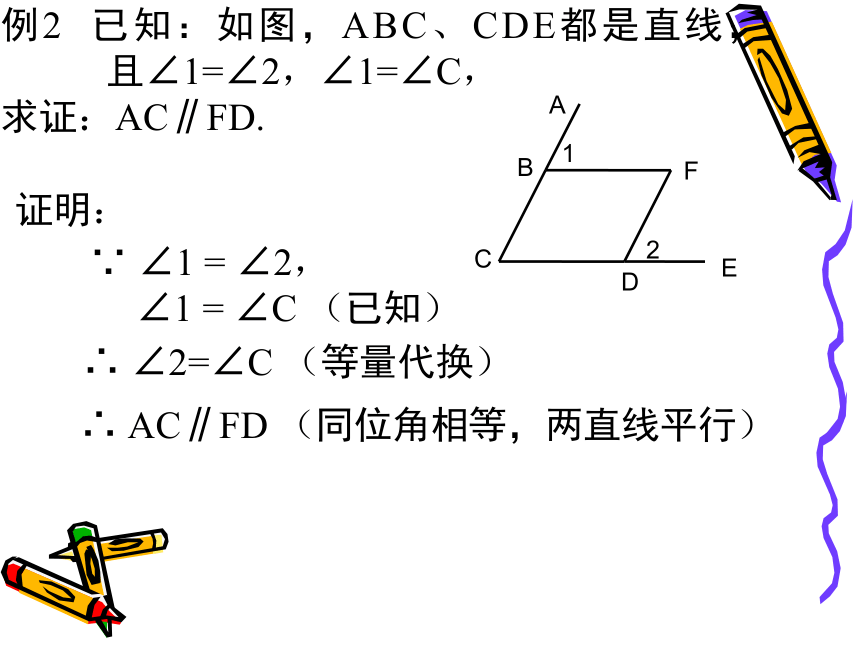
(同位角相等,两直线平行)书写格式:例2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知)
∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) 证明:★如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12(同位角相等,两直线平行).4由上面的推理,你可以得到判定两条直线平行的第二种方法吗?二、发现问题、探究新知 两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.平行线的判定方法2简单说成:内错角相等,两直线平行.号言
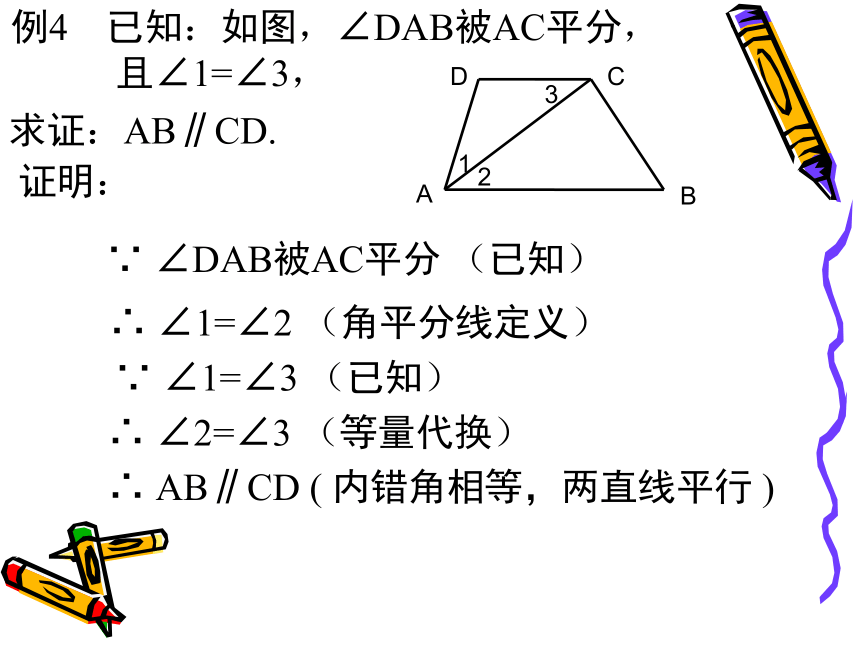
符语(内错角相等,两直线平行)三、展示提升,相互释疑例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:★如图,∠1=∠2 ,∠1=∠3, AB和CD平行吗?为什么?理解与应用★已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两
条直线平行?你的依据是什么?
(2)从∠1=∠C,可以判断哪两条
直线平行?你的依据是什么? ★如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF123 两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.平行线的判定方法3简单说成:同旁内角互补,两直线平行.
语言
符号(同旁内角互补,两直线平行)四、质疑再探,总结点评★如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?并说明理由。答:AB//CD,AD//BC,理由如下:∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC理解与应用 判定两条直线平行的方法同位角内错角同旁内角相等,
两直线平行
∠1=∠2∠3=∠2∠2+∠4=180°abc1234① ∵ ∠1 =_____ (已知)
∴ AB∥CE( )② ∵ ∠2 = (已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2∠4五、运用拓展,达标测评内错角相等,两直线平行同位角相等,两直线平行同旁内角互补,两直线平行∵∠B= ∠1(已知) ∴____∥_____( ) 1ABDC∵∠D= ∠1(已知)
∴____∥_____( ) ADBC同位角相等,两直线平行ABDC内错角相等,两直线平行2.如图,3.如图,
① ∵∠B= ∠C(已知)
∴______∥______
( ) ② ∵∠D+∠BCD=1800 (已知)
∴_______∥________
( )
内错角相等,两直线平行EABCDADBC 同旁内角互补,两直线平行(1)∵∠1 =∠4(已知)
∴____∥____( )
(2)∵∠___= ∠___(已知)
∴BC ∥ EF( )
(3) ∵∠1= ∠___(已知)
∴DE ∥____( ) GCFEBHDA4123GHBC23内错角相等,两直线平行内错角相等,两直线平行2AB内错角相等,两直线平行(1)∵∠A+∠D=180°
∴____∥____( )
(2) ∵∠____+ ∠____=180°
∴AD ∥ ___ ( )ABCD 同旁内角互补,两直线平行DCBC 同旁内角互补,两直线平行 (1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD. (2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系? 图1图2a∥b ABECD12ab 573c10、如右图,∠1=∠2=55°∠3等于多少度?直线AB,CD平行吗?说明你的理由。BDCAEFGH123解∵ ∠1=∠2=55°
∠2=∠3(对顶角相等)
∴ ∠3= 55°(等量代换)
∴ ∠1=∠3 (等量代换)
∴ AB∥CD(同位角相等,两直线平行)例4 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) 证明:
1、理解平行线的三种判定方法,会结合图形用符号语言表示“平行线的判定”的书写格式;
2、经历由“平行线的判定方法一”推导出“平行线的判定方法二、三”的过程,初步体验“简单推理”过程,体会数学中的转化思想;
3、会运用“平行线的判定方法”来判定两条直线是否平行,学会简单的说理。
几何画板.gsp温故知新 两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.平行线的判定方法1简单说成:同位角相等,两直线平行.号言
符语(同位角相等,两直线平行)一、课前预习,明确目标温故知新∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)书写格式:例2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知)
∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) 证明:★如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12(同位角相等,两直线平行).4由上面的推理,你可以得到判定两条直线平行的第二种方法吗?二、发现问题、探究新知 两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.平行线的判定方法2简单说成:内错角相等,两直线平行.号言
符语(内错角相等,两直线平行)三、展示提升,相互释疑例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:★如图,∠1=∠2 ,∠1=∠3, AB和CD平行吗?为什么?理解与应用★已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两
条直线平行?你的依据是什么?
(2)从∠1=∠C,可以判断哪两条
直线平行?你的依据是什么? ★如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF123 两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.平行线的判定方法3简单说成:同旁内角互补,两直线平行.
语言
符号(同旁内角互补,两直线平行)四、质疑再探,总结点评★如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?并说明理由。答:AB//CD,AD//BC,理由如下:∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC理解与应用 判定两条直线平行的方法同位角内错角同旁内角相等,
两直线平行
∠1=∠2∠3=∠2∠2+∠4=180°abc1234① ∵ ∠1 =_____ (已知)
∴ AB∥CE( )② ∵ ∠2 = (已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2∠4五、运用拓展,达标测评内错角相等,两直线平行同位角相等,两直线平行同旁内角互补,两直线平行∵∠B= ∠1(已知) ∴____∥_____( ) 1ABDC∵∠D= ∠1(已知)
∴____∥_____( ) ADBC同位角相等,两直线平行ABDC内错角相等,两直线平行2.如图,3.如图,
① ∵∠B= ∠C(已知)
∴______∥______
( ) ② ∵∠D+∠BCD=1800 (已知)
∴_______∥________
( )
内错角相等,两直线平行EABCDADBC 同旁内角互补,两直线平行(1)∵∠1 =∠4(已知)
∴____∥____( )
(2)∵∠___= ∠___(已知)
∴BC ∥ EF( )
(3) ∵∠1= ∠___(已知)
∴DE ∥____( ) GCFEBHDA4123GHBC23内错角相等,两直线平行内错角相等,两直线平行2AB内错角相等,两直线平行(1)∵∠A+∠D=180°
∴____∥____( )
(2) ∵∠____+ ∠____=180°
∴AD ∥ ___ ( )ABCD 同旁内角互补,两直线平行DCBC 同旁内角互补,两直线平行 (1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD. (2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系? 图1图2a∥b ABECD12ab 573c10、如右图,∠1=∠2=55°∠3等于多少度?直线AB,CD平行吗?说明你的理由。BDCAEFGH123解∵ ∠1=∠2=55°
∠2=∠3(对顶角相等)
∴ ∠3= 55°(等量代换)
∴ ∠1=∠3 (等量代换)
∴ AB∥CD(同位角相等,两直线平行)例4 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) 证明:
