人教版七年级下第五章5.2.2平行线的判定(2)课件(26张PPT)
文档属性
| 名称 | 人教版七年级下第五章5.2.2平行线的判定(2)课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 223.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-02 19:49:17 | ||
图片预览





文档简介
课件26张PPT。5.2.2 平行线的判定
(第2课时)学习目标:
(1)平行线的判定方法的应用;
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力.
学习重点:
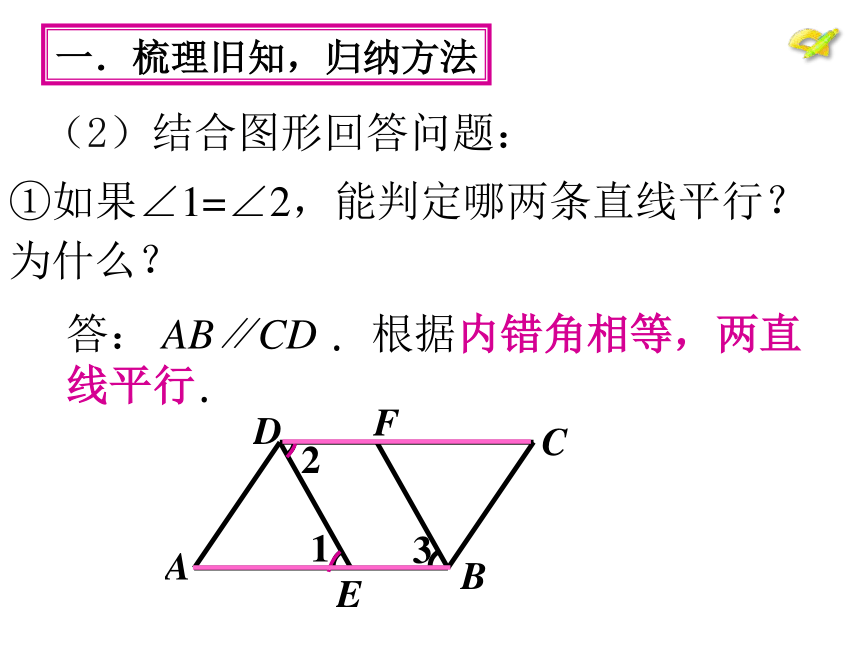
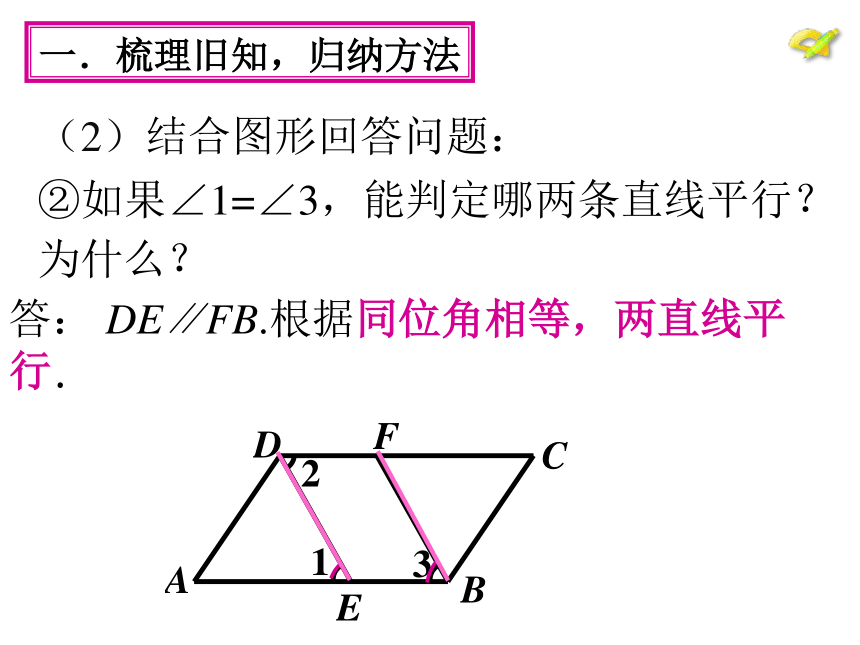
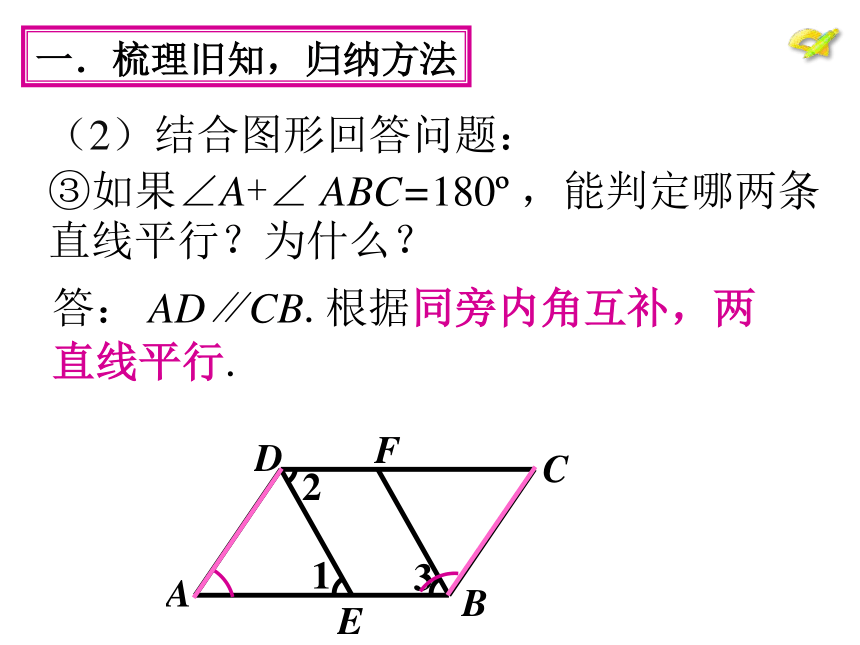
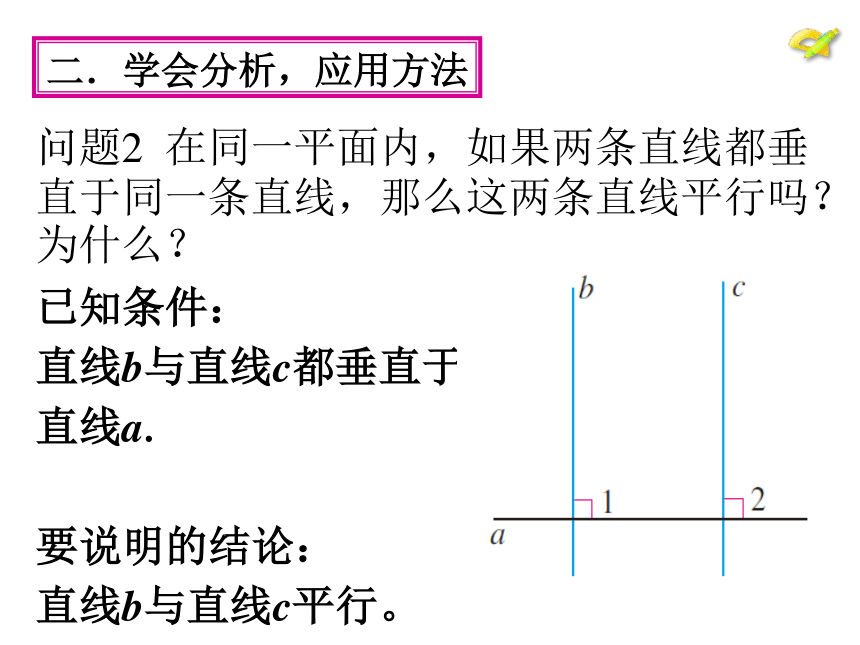
平行线判定方法的应用.根据定义. 根据平行公理的推论.一.梳理旧知,归纳方法问题1(1)判定两条直线平行的方法有哪些? 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.(2)结合图形回答问题:答: AB∥CD .根据内错角相等,两直线平行.一.梳理旧知,归纳方法①如果∠1=∠2,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: DE∥FB.根据同位角相等,两直线平行.一.梳理旧知,归纳方法②如果∠1=∠3,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: AD∥CB.根据同旁内角互补,两直线平行.一.梳理旧知,归纳方法③如果∠A+∠ ABC=180o ,能判定哪两条直线平行?为什么?二.学会分析,应用方法已知条件:
直线b与直线c都垂直于直线a.
要说明的结论:
直线b与直线c平行。问题2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?二.学会分析,应用方法已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:直线b与直线c平行.理由如下:
∵ b⊥a,
∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).二.学会分析,应用方法问题3 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?三.应用迁移,深化理解答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).1. 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?2.已知直线l1,l2被l3所截,?1=45o,?2=135o,判断l1 与 l2 是否平行,并说明理由。解: l1 // l2 理由如下:??? l1 // l2 (同位角相等,两直线平行)由已知,得?2+?3=180o, ?2=135o??3=180o -?2
=180o-135o=45 o 又∵? 1=45o,??1=?3,????a∥bl∥ml∥n 3.当图中各角满足下列条件时,你能指出哪两条直线平行?
(2) ∠2 = ∠4;(3) ∠1 + ∠3 = 180?; (1) ∠1 = ∠4;4.如图∠1=∠2、∠B+∠3=180°
图中哪些线互相平行,为什么?(1)∠2与哪个角相等时,DE∥BC?(2)∠A与哪个角相等时,AB∥EF?3∠2= ∠EFC DE∥BC∠A= ∠FEC AB∥EF内错角相等,两直线平行同位角相等,两直线平行5.如图,已知:∠1=∠2,∠1=∠B, 求证:AB∥EF,DE∥BC。 证明:由∠1=∠2 (已知),
根据: .
得AB∥EF.
又由∠1=∠B( ).
根据:同位角相等,两直线平行
得 ∥ .
内错角相等,两直线平行已知DE BC6.如图,已知:∠1+∠2=180°, 求证:AB∥CD.证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4( ) 根据:等量代换 得:∠3+ =180°.
根据:同旁内角互补,两直线平行
得: ∥ .对顶角相等∠4AB CD7.如图,已知:∠DAF=∠AFE,∠ADC+∠DCB=180°,求证:EF∥BC证明:由:∠DAF=∠AFE ( )
根据: .
得:AD∥ .
由:∠ADC+ =180°(已知).
根据: .
得:AD∥ .
再根据: .
得:EF∥BC已知内错角相等,两直线平行EF∠DCB同旁内角互补,两直线平行BC平行于同一直线的两条直线互相平行8.如图,已知:∠2=∠3,∠1+∠3=180°, 求证:EF∥GH. 证明:由:∠2=∠3 (已知) ∠1+∠3=180°( )
根据: .
得:∠1+∠2=180°.
根据: .
得: 。已知等量代换同旁内角互补,两直线平行EF∥GH证明:由BD平分∠ABC(已知),
根据: .
得:∠2=∠3.
又由:∠2=∠1(已知)
根据: .
得:∠3= .
根据:内错角相等,两直线平行.
得: ∥ .9.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC. 角平分线定义等量代换∠1AD BC10.如图,已知:AB∥CD,∠1=55°∠2=80°, 求∠3的度数. 11.如图,直线AB过点C, ∠2=70°, ∠D=55°, ∠ 1=∠3. AB∥DE吗?为什么?12.如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?13.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E. 证明:由 (已知),
根据:两直线平行,内错角相等
得:∠ABD= .
由AE∥BD( ).
根据: .
得∠BDC=∠E .
再根据:等量代换
得: = .AB∥CD∠ BDC已知两直线平行,同位角相等∠ ABD ∠E14.如图,已知:AC∥DE,∠1=∠2,试说明AB∥CD. 证明:由AC∥DE (已知),
根据:两直线平行,内错角相等.
得∠ACD= .
又由∠1=∠2(已知).
根据: .
得∠1=∠ACD .
再根据: .
得 ∥ .∠ 2等量代换内错角相等,两直线平行AB CD15.如图,已知:AB∥CD,∠A=70°∠DHE=70°,求证:AM∥EF(1)平行线的判定方法有哪些?4.归纳小结(2)结合例题,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?教科书 习题5.2 第6、10、12题5.布置作业
(1)平行线的判定方法的应用;
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力.
学习重点:
平行线判定方法的应用.根据定义. 根据平行公理的推论.一.梳理旧知,归纳方法问题1(1)判定两条直线平行的方法有哪些? 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.(2)结合图形回答问题:答: AB∥CD .根据内错角相等,两直线平行.一.梳理旧知,归纳方法①如果∠1=∠2,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: DE∥FB.根据同位角相等,两直线平行.一.梳理旧知,归纳方法②如果∠1=∠3,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: AD∥CB.根据同旁内角互补,两直线平行.一.梳理旧知,归纳方法③如果∠A+∠ ABC=180o ,能判定哪两条直线平行?为什么?二.学会分析,应用方法已知条件:
直线b与直线c都垂直于直线a.
要说明的结论:
直线b与直线c平行。问题2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?二.学会分析,应用方法已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:直线b与直线c平行.理由如下:
∵ b⊥a,
∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).二.学会分析,应用方法问题3 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?三.应用迁移,深化理解答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).1. 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?2.已知直线l1,l2被l3所截,?1=45o,?2=135o,判断l1 与 l2 是否平行,并说明理由。解: l1 // l2 理由如下:??? l1 // l2 (同位角相等,两直线平行)由已知,得?2+?3=180o, ?2=135o??3=180o -?2
=180o-135o=45 o 又∵? 1=45o,??1=?3,????a∥bl∥ml∥n 3.当图中各角满足下列条件时,你能指出哪两条直线平行?
(2) ∠2 = ∠4;(3) ∠1 + ∠3 = 180?; (1) ∠1 = ∠4;4.如图∠1=∠2、∠B+∠3=180°
图中哪些线互相平行,为什么?(1)∠2与哪个角相等时,DE∥BC?(2)∠A与哪个角相等时,AB∥EF?3∠2= ∠EFC DE∥BC∠A= ∠FEC AB∥EF内错角相等,两直线平行同位角相等,两直线平行5.如图,已知:∠1=∠2,∠1=∠B, 求证:AB∥EF,DE∥BC。 证明:由∠1=∠2 (已知),
根据: .
得AB∥EF.
又由∠1=∠B( ).
根据:同位角相等,两直线平行
得 ∥ .
内错角相等,两直线平行已知DE BC6.如图,已知:∠1+∠2=180°, 求证:AB∥CD.证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4( ) 根据:等量代换 得:∠3+ =180°.
根据:同旁内角互补,两直线平行
得: ∥ .对顶角相等∠4AB CD7.如图,已知:∠DAF=∠AFE,∠ADC+∠DCB=180°,求证:EF∥BC证明:由:∠DAF=∠AFE ( )
根据: .
得:AD∥ .
由:∠ADC+ =180°(已知).
根据: .
得:AD∥ .
再根据: .
得:EF∥BC已知内错角相等,两直线平行EF∠DCB同旁内角互补,两直线平行BC平行于同一直线的两条直线互相平行8.如图,已知:∠2=∠3,∠1+∠3=180°, 求证:EF∥GH. 证明:由:∠2=∠3 (已知) ∠1+∠3=180°( )
根据: .
得:∠1+∠2=180°.
根据: .
得: 。已知等量代换同旁内角互补,两直线平行EF∥GH证明:由BD平分∠ABC(已知),
根据: .
得:∠2=∠3.
又由:∠2=∠1(已知)
根据: .
得:∠3= .
根据:内错角相等,两直线平行.
得: ∥ .9.如图,已知:∠1=∠2,BD平分∠ABC,试说明AD∥BC. 角平分线定义等量代换∠1AD BC10.如图,已知:AB∥CD,∠1=55°∠2=80°, 求∠3的度数. 11.如图,直线AB过点C, ∠2=70°, ∠D=55°, ∠ 1=∠3. AB∥DE吗?为什么?12.如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?13.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E. 证明:由 (已知),
根据:两直线平行,内错角相等
得:∠ABD= .
由AE∥BD( ).
根据: .
得∠BDC=∠E .
再根据:等量代换
得: = .AB∥CD∠ BDC已知两直线平行,同位角相等∠ ABD ∠E14.如图,已知:AC∥DE,∠1=∠2,试说明AB∥CD. 证明:由AC∥DE (已知),
根据:两直线平行,内错角相等.
得∠ACD= .
又由∠1=∠2(已知).
根据: .
得∠1=∠ACD .
再根据: .
得 ∥ .∠ 2等量代换内错角相等,两直线平行AB CD15.如图,已知:AB∥CD,∠A=70°∠DHE=70°,求证:AM∥EF(1)平行线的判定方法有哪些?4.归纳小结(2)结合例题,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?教科书 习题5.2 第6、10、12题5.布置作业
