人教版八年级数学下册 17.1 勾股定理 第1课时 勾股定理 课件(15张)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理 第1课时 勾股定理 课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 631.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 01:29:41 | ||
图片预览



文档简介
(共15张PPT)
17.1 勾股定理
第十七章 勾股定理
第1课时 勾股定理
学习目标
1.掌握勾股定理,会用面积法加以证明.(重点)
2.会用勾股定理进行简单的计算 .(难点)
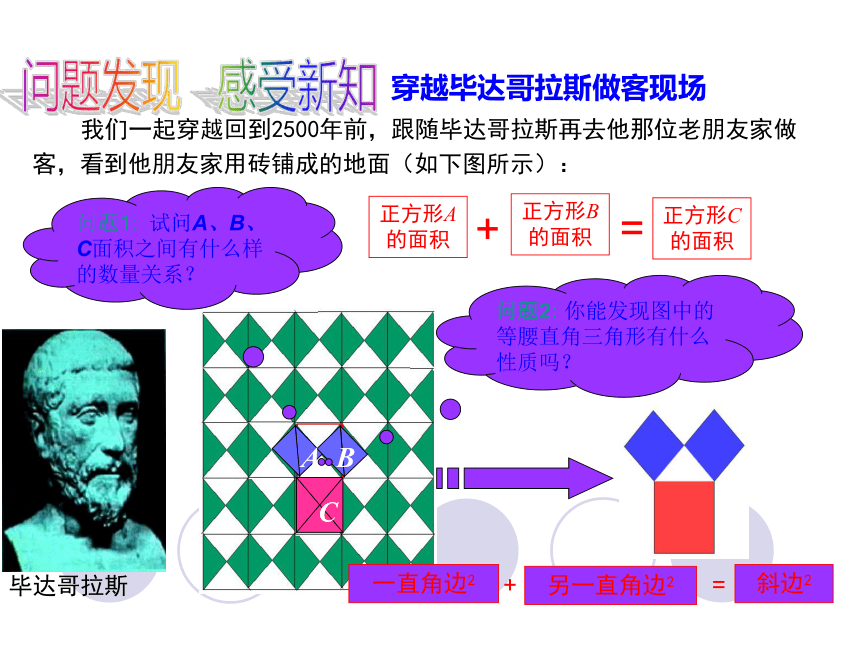
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用砖铺成的地面(如下图所示):
毕达哥拉斯
A
B
C
穿越毕达哥拉斯做客现场
正方形A的面积
正方形B的面积
正方形C的面积
+
=
问题发现 感受新知
问题1: 试问A、B、C面积之间有什么样的数量关系?
问题2: 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
图1-2
图①
图②
A
B
A
B
C
C
正方形A的面积
正方形B的面积
正方形C的面积
+
=
一直角边2
另一直角边2
斜边2
+
=
问题发现 感受新知
问题3 图中每个小方格的面积均为1,请分别计算出图①、②中A、B、C的面积,看看能得出什么结论?
问题4 图中的直角三角形的三边有什么样的数量关系?
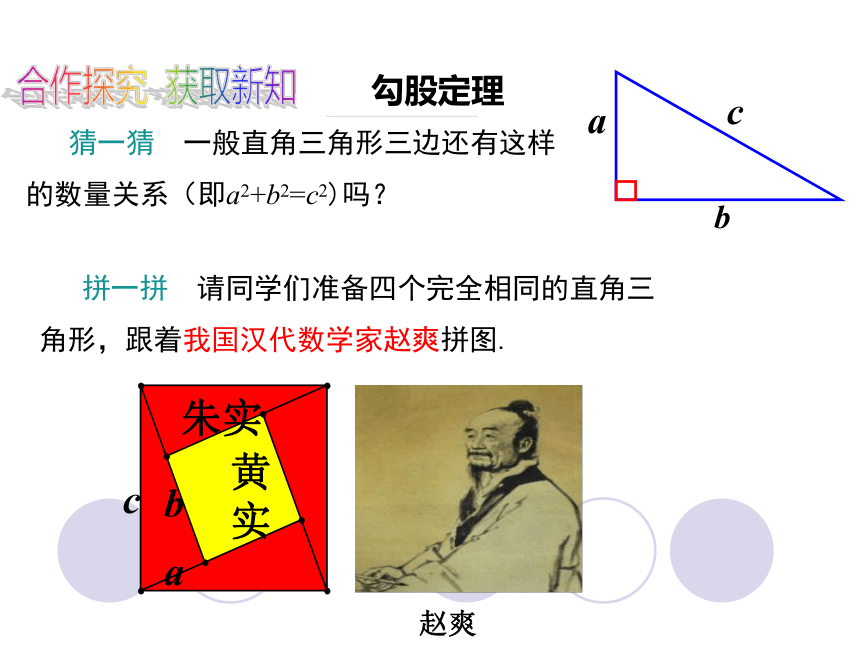
猜一猜 一般直角三角形三边还有这样
的数量关系(即a2+b2=c2)吗?
a
b
c
勾股定理
合作探究 获取新知
拼一拼 请同学们准备四个完全相同的直角三角形,跟着我国汉代数学家赵爽拼图.
赵爽
c
b
a
黄
实
朱实
a
b
b
c
a
b
c
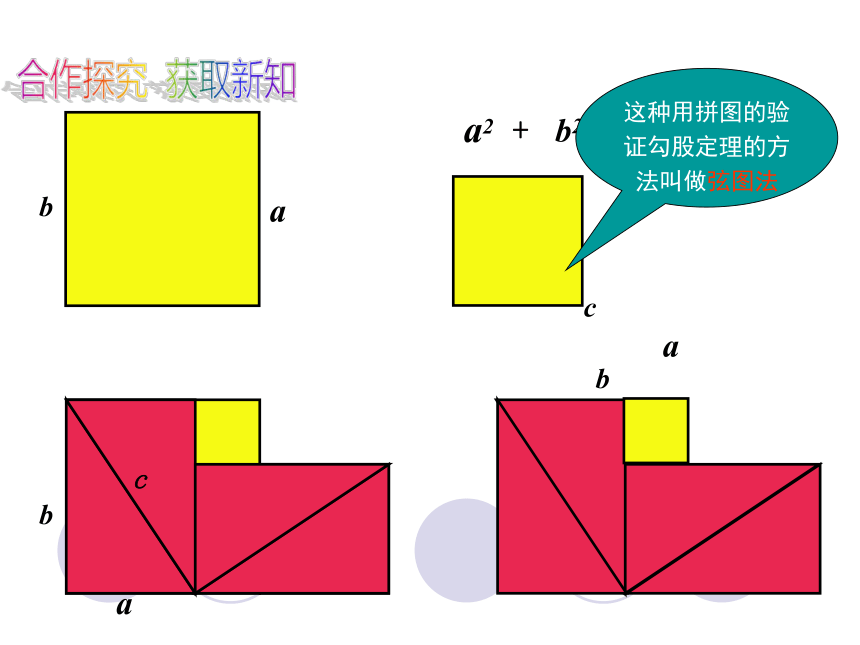
c2
b2
a2
=
+
这种用拼图的验证勾股定理的方法叫做弦图法
a
合作探究 获取新知
a
b
c
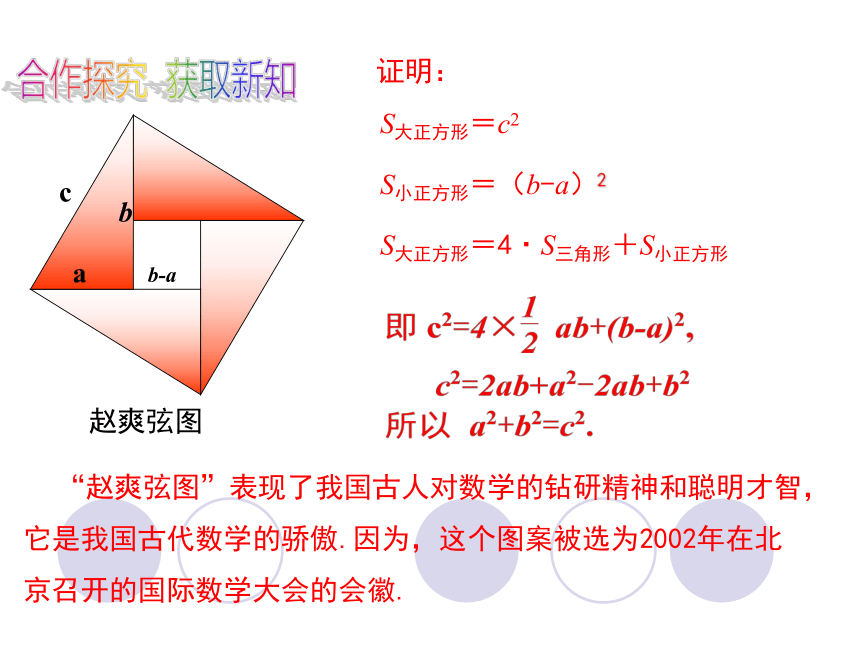
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
合作探究 获取新知
赵爽所用的这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
赵爽弦图
c
b
a
黄
实
朱实
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际.以至于古往今来,上至帝王总统都愿意探讨、研究它的证明,新的证法不断出现.建议同学们课外认真阅读P30《勾股定理的证明》.
合作探究 获取新知
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾
股
弦
即:勾2+股2=弦2
勾股定理
合作探究 获取新知
例1 在Rt△ABC中, ∠C=90°
(1)已知a=b=5,求c;
(2)已知a=1,c=2,求b;
解:
(1)据勾股定理得
(2)据勾股定理得
实战演练 运用新知
(3)已知a:b=1:2 ,c=5,求a;
(4)已知b=15,∠A=30°,求a,c.
在Rt△ABC中, ∠C=90°
解:
(3)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52
解得
(4)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152
解得
例2 已知:Rt△ABC中,AB=4,AC=3,则BC= .
5 或
4
3
A
C
B
4
3
C
A
B
温馨提示 当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,否则容易丢解.
实战演练 运用新知
1.如图所示,字母B所代表的正方形的面积是( )
A.12 B.13 C.144 D.194
C
2.下列说法中正确的是( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
巩固新知 深化理解
3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是 .
4.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为 .
25或7
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
回顾与反思
看似平淡无奇的现象有时却隐藏着深刻的道理
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
回顾
?
17.1 勾股定理
第十七章 勾股定理
第1课时 勾股定理
学习目标
1.掌握勾股定理,会用面积法加以证明.(重点)
2.会用勾股定理进行简单的计算 .(难点)
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用砖铺成的地面(如下图所示):
毕达哥拉斯
A
B
C
穿越毕达哥拉斯做客现场
正方形A的面积
正方形B的面积
正方形C的面积
+
=
问题发现 感受新知
问题1: 试问A、B、C面积之间有什么样的数量关系?
问题2: 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
图1-2
图①
图②
A
B
A
B
C
C
正方形A的面积
正方形B的面积
正方形C的面积
+
=
一直角边2
另一直角边2
斜边2
+
=
问题发现 感受新知
问题3 图中每个小方格的面积均为1,请分别计算出图①、②中A、B、C的面积,看看能得出什么结论?
问题4 图中的直角三角形的三边有什么样的数量关系?
猜一猜 一般直角三角形三边还有这样
的数量关系(即a2+b2=c2)吗?
a
b
c
勾股定理
合作探究 获取新知
拼一拼 请同学们准备四个完全相同的直角三角形,跟着我国汉代数学家赵爽拼图.
赵爽
c
b
a
黄
实
朱实
a
b
b
c
a
b
c
c2
b2
a2
=
+
这种用拼图的验证勾股定理的方法叫做弦图法
a
合作探究 获取新知
a
b
c
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
合作探究 获取新知
赵爽所用的这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
赵爽弦图
c
b
a
黄
实
朱实
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际.以至于古往今来,上至帝王总统都愿意探讨、研究它的证明,新的证法不断出现.建议同学们课外认真阅读P30《勾股定理的证明》.
合作探究 获取新知
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾
股
弦
即:勾2+股2=弦2
勾股定理
合作探究 获取新知
例1 在Rt△ABC中, ∠C=90°
(1)已知a=b=5,求c;
(2)已知a=1,c=2,求b;
解:
(1)据勾股定理得
(2)据勾股定理得
实战演练 运用新知
(3)已知a:b=1:2 ,c=5,求a;
(4)已知b=15,∠A=30°,求a,c.
在Rt△ABC中, ∠C=90°
解:
(3)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52
解得
(4)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152
解得
例2 已知:Rt△ABC中,AB=4,AC=3,则BC= .
5 或
4
3
A
C
B
4
3
C
A
B
温馨提示 当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,否则容易丢解.
实战演练 运用新知
1.如图所示,字母B所代表的正方形的面积是( )
A.12 B.13 C.144 D.194
C
2.下列说法中正确的是( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
巩固新知 深化理解
3.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是 .
4.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为 .
25或7
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
回顾与反思
看似平淡无奇的现象有时却隐藏着深刻的道理
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
回顾
?
