3.5综合与实践——探索图形 同步课件
图片预览

文档简介
(共15张PPT)
3.5 综合与实践
——探索图形
人教版 五年级下
新知导入
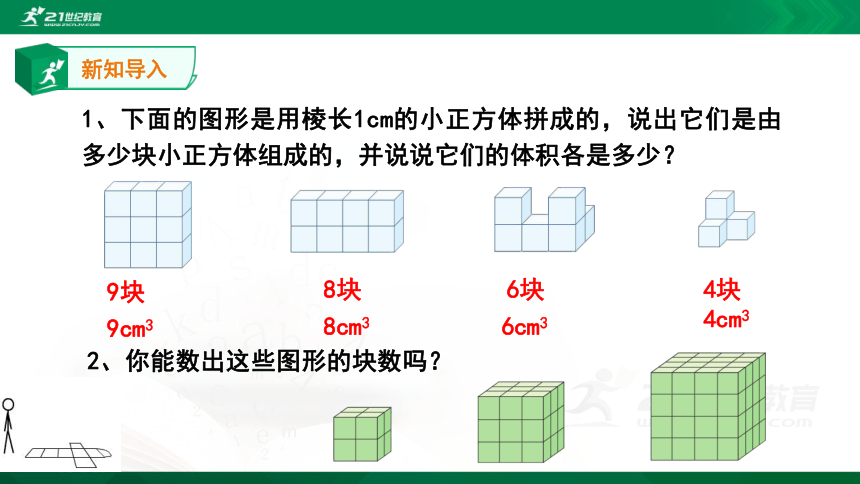
1、下面的图形是用棱长1cm的小正方体拼成的,说出它们是由多少块小正方体组成的,并说说它们的体积各是多少?
9cm3
8cm3
6cm3
4cm3
9块
8块
6块
4块
2、你能数出这些图形的块数吗?
新知讲解
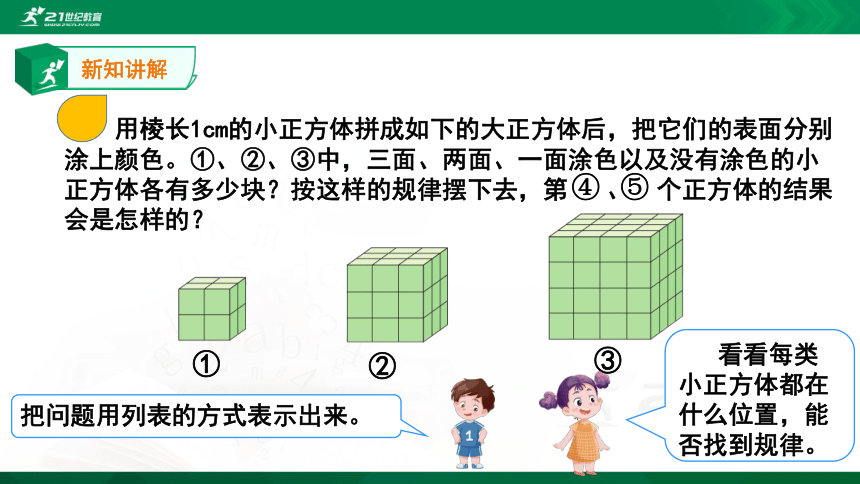
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别
涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?按这样的规律摆下去,第 、 个正方体的结果会是怎样的?
④
⑤
①
②
③
把问题用列表的方式表示出来。
看看每类小正方体都在什么位置,能否找到规律。
新知讲解
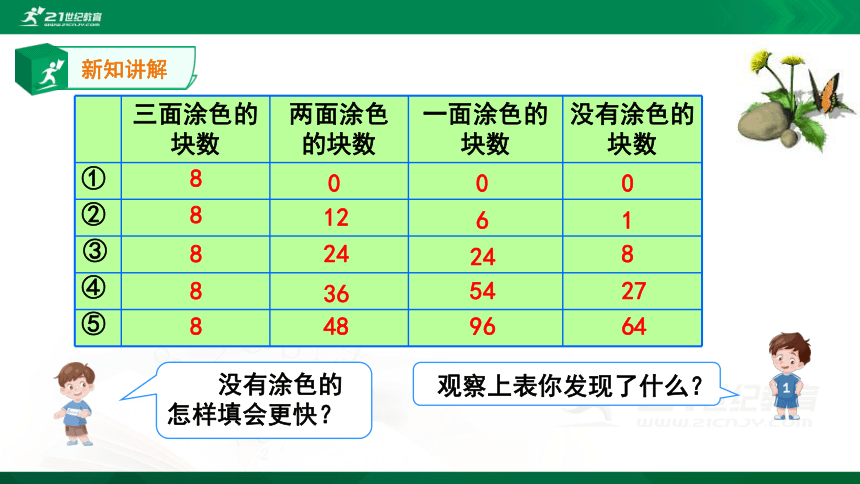
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8
36
54
27
8
48
96
64
①
②
③
④
⑤
8
8
8
24
12
0
0
0
8
1
24
6
没有涂色的怎样填会更快?
观察上表你发现了什么?
新知讲解
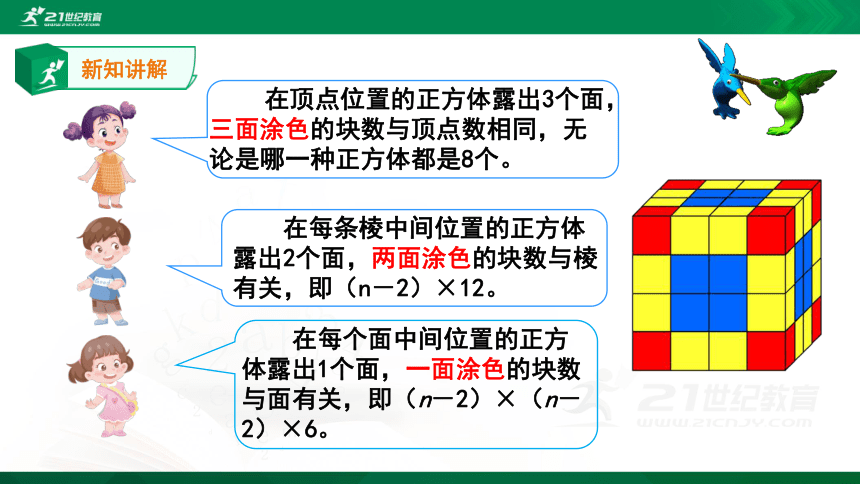
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
新知讲解
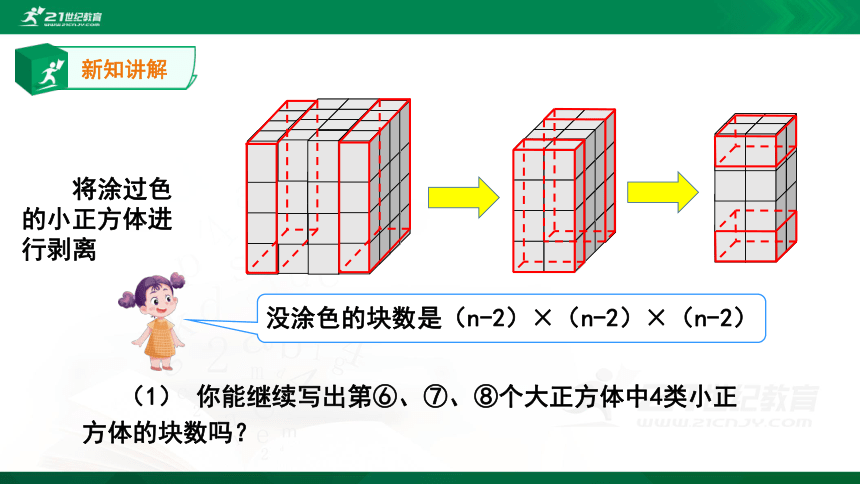
将涂过色的小正方体进行剥离
没涂色的块数是(n-2)×(n-2)×(n-2)
(1) 你能继续写出第⑥、⑦、⑧个大正方体中4类小正方体的块数吗?
新知讲解
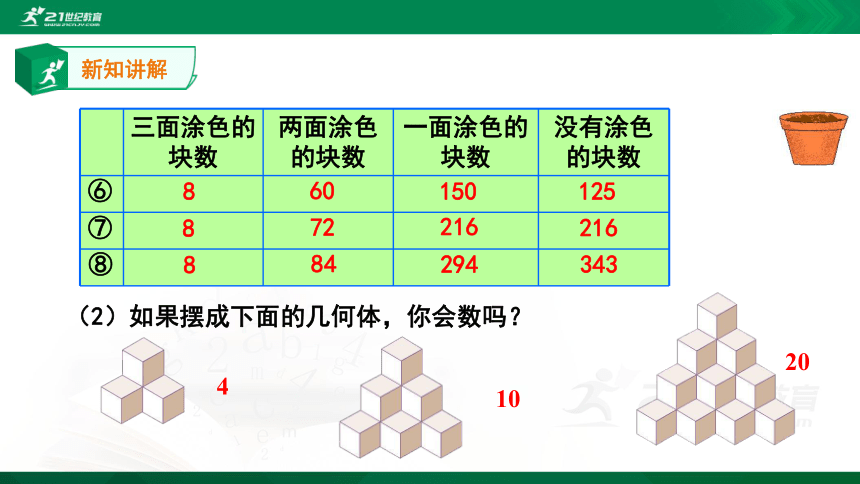
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8
60
150
125
8
72
216
216
8
84
294
343
⑥
⑦
⑧
(2)如果摆成下面的几何体,你会数吗?
4
10
20
课堂练习
1、一个正方体,先在它的每个面都涂上红色,再把它刚好切成棱长是1cm的小正方体。已知两面涂色的小正方体有96个,这个正方体的体积是多少立方厘米
分析:根据已学的结论知道两面涂色跟棱长有关,则用(n-2)×12,可以求出正方体的边长。
96÷12+2=10(cm)
10×10×10
=1000(立方厘米)
答:这个正方体的体积是1000立方厘米。
课堂练习
2、如图,下列几何体都是由若干个边长为1cm的小正方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第2016个几何体中只有两个面涂色的小正方体共有多少个
分析:根据图形观察两面涂色任然跟棱长有关,由于底面不涂色,则底面棱长就只有固定的4个两面涂色,在顶点处,而竖起的四条棱和上面的四条棱任然符合规律为(n-2)×4
课堂练习
3、数一数。
( )个正方体
( )个正方体
17
13
答:第2016个几何体中只有两个面涂色的小正方体共有16124个。
(n-2)×4+(n-2)×4+4
=(n-2)×8+4
由于个数与边长相差1,当第2016个图形时,正方体的边长为n=2017
(n-2)×8+4
=16124(个)
课堂练习
4、一张长方形铁皮,长是32cm,在它的四个角上分别剪去边长是4cm的正方形后,焊接成一个无盖的长方体铁皮盒。这个长方体铁皮盒的容积是768mL,原来这张铁皮的面积是多少?(铁皮的厚度忽略不计)
768mL=768cm3
768÷(32-4×2)÷4
铁皮盒的宽:
长方形铁皮的宽:
4×2+8=16(cm)
32×16=512(cm2)
答:原来这张铁皮的面积是512cm2。
=8(cm)
课堂总结
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别
涂上颜色。三面、两面、一面涂色以及没有涂色的小正方体有以下规律:
1、三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
2、两面涂色的块数与棱有关,即(n-2)×12。
3、一面涂色的块数与面有关,即(n-2)×(n-2)×6。
4、没涂色的块数是(n-2)×(n-2)×(n-2)
作业布置
2、探究生活中的图形规律。
1、完成相应课时练习册。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
3.5 综合与实践
——探索图形
人教版 五年级下
新知导入
1、下面的图形是用棱长1cm的小正方体拼成的,说出它们是由多少块小正方体组成的,并说说它们的体积各是多少?
9cm3
8cm3
6cm3
4cm3
9块
8块
6块
4块
2、你能数出这些图形的块数吗?
新知讲解
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别
涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?按这样的规律摆下去,第 、 个正方体的结果会是怎样的?
④
⑤
①
②
③
把问题用列表的方式表示出来。
看看每类小正方体都在什么位置,能否找到规律。
新知讲解
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8
36
54
27
8
48
96
64
①
②
③
④
⑤
8
8
8
24
12
0
0
0
8
1
24
6
没有涂色的怎样填会更快?
观察上表你发现了什么?
新知讲解
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
新知讲解
将涂过色的小正方体进行剥离
没涂色的块数是(n-2)×(n-2)×(n-2)
(1) 你能继续写出第⑥、⑦、⑧个大正方体中4类小正方体的块数吗?
新知讲解
三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
8
60
150
125
8
72
216
216
8
84
294
343
⑥
⑦
⑧
(2)如果摆成下面的几何体,你会数吗?
4
10
20
课堂练习
1、一个正方体,先在它的每个面都涂上红色,再把它刚好切成棱长是1cm的小正方体。已知两面涂色的小正方体有96个,这个正方体的体积是多少立方厘米
分析:根据已学的结论知道两面涂色跟棱长有关,则用(n-2)×12,可以求出正方体的边长。
96÷12+2=10(cm)
10×10×10
=1000(立方厘米)
答:这个正方体的体积是1000立方厘米。
课堂练习
2、如图,下列几何体都是由若干个边长为1cm的小正方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第2016个几何体中只有两个面涂色的小正方体共有多少个
分析:根据图形观察两面涂色任然跟棱长有关,由于底面不涂色,则底面棱长就只有固定的4个两面涂色,在顶点处,而竖起的四条棱和上面的四条棱任然符合规律为(n-2)×4
课堂练习
3、数一数。
( )个正方体
( )个正方体
17
13
答:第2016个几何体中只有两个面涂色的小正方体共有16124个。
(n-2)×4+(n-2)×4+4
=(n-2)×8+4
由于个数与边长相差1,当第2016个图形时,正方体的边长为n=2017
(n-2)×8+4
=16124(个)
课堂练习
4、一张长方形铁皮,长是32cm,在它的四个角上分别剪去边长是4cm的正方形后,焊接成一个无盖的长方体铁皮盒。这个长方体铁皮盒的容积是768mL,原来这张铁皮的面积是多少?(铁皮的厚度忽略不计)
768mL=768cm3
768÷(32-4×2)÷4
铁皮盒的宽:
长方形铁皮的宽:
4×2+8=16(cm)
32×16=512(cm2)
答:原来这张铁皮的面积是512cm2。
=8(cm)
课堂总结
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别
涂上颜色。三面、两面、一面涂色以及没有涂色的小正方体有以下规律:
1、三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
2、两面涂色的块数与棱有关,即(n-2)×12。
3、一面涂色的块数与面有关,即(n-2)×(n-2)×6。
4、没涂色的块数是(n-2)×(n-2)×(n-2)
作业布置
2、探究生活中的图形规律。
1、完成相应课时练习册。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
