2019-2020学年数学新人教A版必修4学案:2.2.1向量加法运算及其几何意义Word版含答案
文档属性
| 名称 | 2019-2020学年数学新人教A版必修4学案:2.2.1向量加法运算及其几何意义Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 146.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览

文档简介
2.2.1向量加法运算及其几何意义
一、三维目标
知识与技能:1.理解向量加法的含义,会用向量加法的三角形法则和平行四边形法则作两个向量的和.2.通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,表述两个运算律的几何意义,并会用它们进行向量计算。
过程与方法:通过学生探究问题,指导学生发现知识结论,培养学生抽象概括能力和逻辑思维能力。
情感态度与价值观:通过本节学习,使同学们对向量加法的三角形法则和平行四边形法则有一定的认识,进一步让学生理解和领悟数形结合的思想。
二、教学重、难点
重点:如何作两个向量的和向量。
难点:对向量加法定义的理解。
三、学法指导
认真阅读教材本节内容,在理解向量加法的三角形法则和四边形法则及其几何意义的基础上,完成相应习题,并体会数形结合思想在本节课的应用。
四、知识链接
1.向量的概念:
2.平行向量、相等向量的概念:
五、学习过程:
1.阅读教材P80—P81页,得到向量加法的定义:
求两个向量和的运算叫做向量的加法。 表示:=.
【注意】:两个向量的和仍是向量,简称和向量。
规定:零向量与任一向量,都有.
2.向量的加法法则
几何中向量加法是用几何作图来定义的,一般有两种方法,即向量加法的三角形法则和平行四边形法则(对于两个向量共线不适应)。
1).三角形法则:根据向量加法定义得到的求向量和的方法(“首尾相接,首尾连”),称为向量加法的三角形法则。表示:=.
2).平行四边形法则:以同一点为起点的两个已知向量,为邻边作平行四边形,则以为起点的对角线就是与的和,这种求向量和的方法称为向量加法的平行四边形法则。
【说明】:教材中采用了三角形法则来定义,这种定义,对两向量共线时同样适用,当向量不共线时,向量加法的三角形法则和平行四边形法则是一致的。
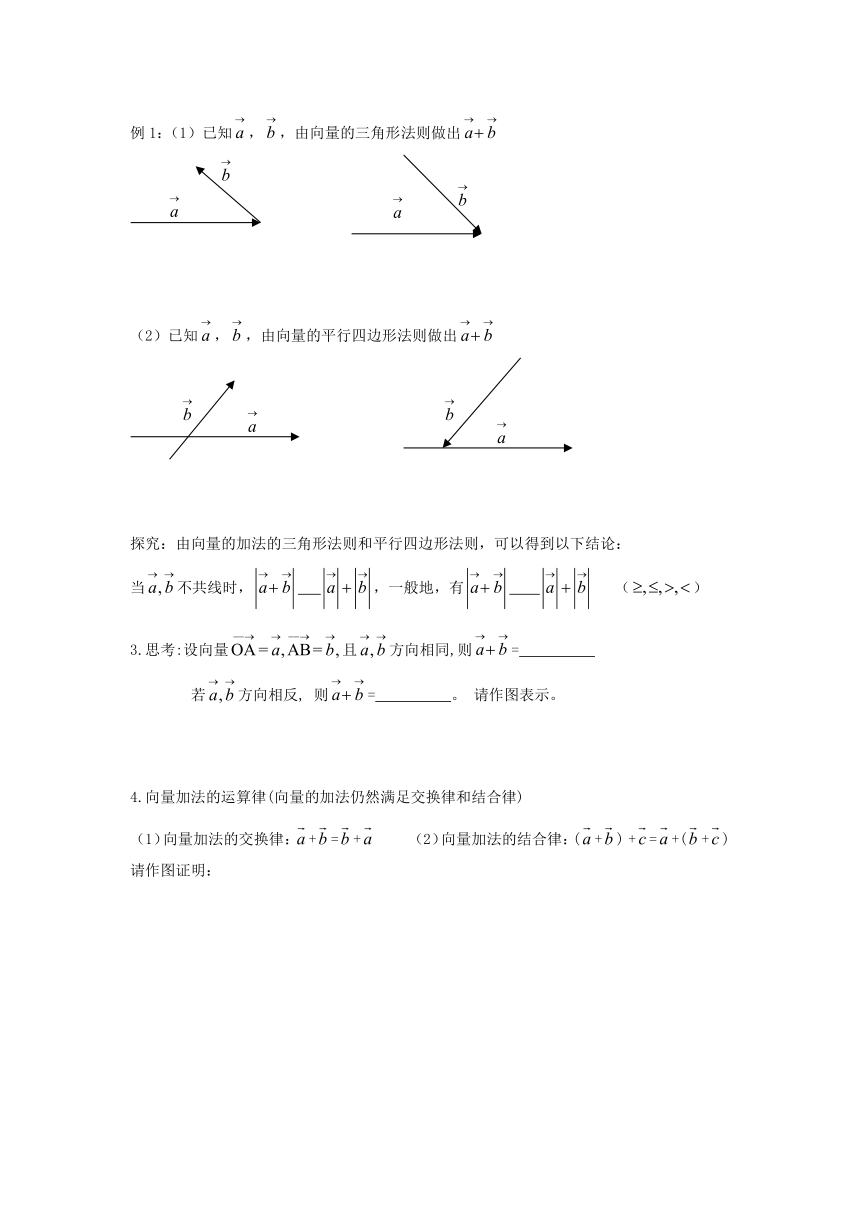
例1:(1)已知,,由向量的三角形法则做出
(2)已知,,由向量的平行四边形法则做出
探究:由向量的加法的三角形法则和平行四边形法则,可以得到以下结论:
当不共线时, ,一般地,有 ()
3.思考:设向量且方向相同,则=
若方向相反, 则= 。 请作图表示。
4.向量加法的运算律(向量的加法仍然满足交换律和结合律)
(1)向量加法的交换律:+=+ (2)向量加法的结合律:(+) +=+(+)
请作图证明:
注:由向量加法的结合律可知,多个向量的加法运算可以按照任意的次序、任意的组合来进行。
例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,如图所示,一艘船从长江南岸A点出发,以km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h。
(1)试用向量表示江水速度、船速以及船实际航行的速度;(保留两个有效数字)
(2)求船实际航行的速度的大小与方向(用与江水速度的夹角来表示)。
六、达标训练:
A1.根据图示填空:
A2.化简:
(1) (2)
(3)
B3.已知正方形ABCD的边长为1,,,,则a+b+c的模等于( )
A.0 B. C. D.
七、归纳小结:
八、课后反思:
2.2.1向量加法运算及其几何意义《答案》
例1:略
例2:
答:船实际航行速度为4km/h,方向与水的流速间的夹角为60o。
达标检测
1. (1) (2) (3) (4)
2. (1) (2) (3)
3解析:如图,a+b=c,
故a+b+c=2c.
∴.
答案:D
一、三维目标
知识与技能:1.理解向量加法的含义,会用向量加法的三角形法则和平行四边形法则作两个向量的和.2.通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,表述两个运算律的几何意义,并会用它们进行向量计算。
过程与方法:通过学生探究问题,指导学生发现知识结论,培养学生抽象概括能力和逻辑思维能力。
情感态度与价值观:通过本节学习,使同学们对向量加法的三角形法则和平行四边形法则有一定的认识,进一步让学生理解和领悟数形结合的思想。
二、教学重、难点
重点:如何作两个向量的和向量。
难点:对向量加法定义的理解。
三、学法指导
认真阅读教材本节内容,在理解向量加法的三角形法则和四边形法则及其几何意义的基础上,完成相应习题,并体会数形结合思想在本节课的应用。
四、知识链接
1.向量的概念:
2.平行向量、相等向量的概念:
五、学习过程:
1.阅读教材P80—P81页,得到向量加法的定义:
求两个向量和的运算叫做向量的加法。 表示:=.
【注意】:两个向量的和仍是向量,简称和向量。
规定:零向量与任一向量,都有.
2.向量的加法法则
几何中向量加法是用几何作图来定义的,一般有两种方法,即向量加法的三角形法则和平行四边形法则(对于两个向量共线不适应)。
1).三角形法则:根据向量加法定义得到的求向量和的方法(“首尾相接,首尾连”),称为向量加法的三角形法则。表示:=.
2).平行四边形法则:以同一点为起点的两个已知向量,为邻边作平行四边形,则以为起点的对角线就是与的和,这种求向量和的方法称为向量加法的平行四边形法则。
【说明】:教材中采用了三角形法则来定义,这种定义,对两向量共线时同样适用,当向量不共线时,向量加法的三角形法则和平行四边形法则是一致的。
例1:(1)已知,,由向量的三角形法则做出
(2)已知,,由向量的平行四边形法则做出
探究:由向量的加法的三角形法则和平行四边形法则,可以得到以下结论:
当不共线时, ,一般地,有 ()
3.思考:设向量且方向相同,则=
若方向相反, 则= 。 请作图表示。
4.向量加法的运算律(向量的加法仍然满足交换律和结合律)
(1)向量加法的交换律:+=+ (2)向量加法的结合律:(+) +=+(+)
请作图证明:
注:由向量加法的结合律可知,多个向量的加法运算可以按照任意的次序、任意的组合来进行。
例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,如图所示,一艘船从长江南岸A点出发,以km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h。
(1)试用向量表示江水速度、船速以及船实际航行的速度;(保留两个有效数字)
(2)求船实际航行的速度的大小与方向(用与江水速度的夹角来表示)。
六、达标训练:
A1.根据图示填空:
A2.化简:
(1) (2)
(3)
B3.已知正方形ABCD的边长为1,,,,则a+b+c的模等于( )
A.0 B. C. D.
七、归纳小结:
八、课后反思:
2.2.1向量加法运算及其几何意义《答案》
例1:略
例2:
答:船实际航行速度为4km/h,方向与水的流速间的夹角为60o。
达标检测
1. (1) (2) (3) (4)
2. (1) (2) (3)
3解析:如图,a+b=c,
故a+b+c=2c.
∴.
答案:D
