2019-2020学年数学新人教A版必修4学案:2.4.2平面向量数量积的坐标表示、模、夹角Word版含答案
文档属性
| 名称 | 2019-2020学年数学新人教A版必修4学案:2.4.2平面向量数量积的坐标表示、模、夹角Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 64.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 12:22:36 | ||
图片预览

文档简介
2.4.2平面向量数量积的坐标表示、模、夹角
一、三维目标:
知识与技能:掌握平面向量数量积的坐标表示;掌握两个向量垂直的坐标条件以及能运用 两个向量的数量积的坐标表示解决有关长度、角度、垂直等几何问题。
过程与方法:通过平面向量数量积的坐标表示,进一步加深对平面向量数量积的认识,提高学生的运算速度。
情感态度与价值观:培养运算能力,创新能力,提高数学素质。
二、学习重、难点:
重点:平面向量数量积的坐标表示。
难点:平面向量数量积的坐标表示的综合运用。
三、学法指导:通过数量积的坐标表示的学习,会求夹角及两点间距离公式。
四、知识链接:
1.平面向量数量积(内积)的定义:已知两个非零向量与,它们的夹角是,则数量,叫与的数量积,记作,即有,。并规定与任何向量的数量积为0.
2.向量的数量积的几何意义:
数量积等于的长度与在方向上投影的乘积。
3.两个向量的数量积的性质:设、为两个非零向量,是与同向的单位向量。
1? ; 2?
3? 当与同向时,;当与反向时,。 特别的或4? cos? = ;5?
5.平面向量数量积的运算律
交换律:
数乘结合律:
分配律:
五、学习过程:
问题1.在直角坐标系中,已知两个非零向量=(x1,y1),=(x2,y2),如何用与的坐标表示
(x轴上的单位向量,y轴上的单位向量)
这就是说:
问题2. 平面内两点间的距离公式
设,则( )或( )
(2)如果表示向量的有向线段的起点和终点的坐标分别为、,那么
(平面内两点间的距离公式)
问题3 向量垂直的判定
设,,则( )
问题4两向量夹角的余弦()
cos? = ( )
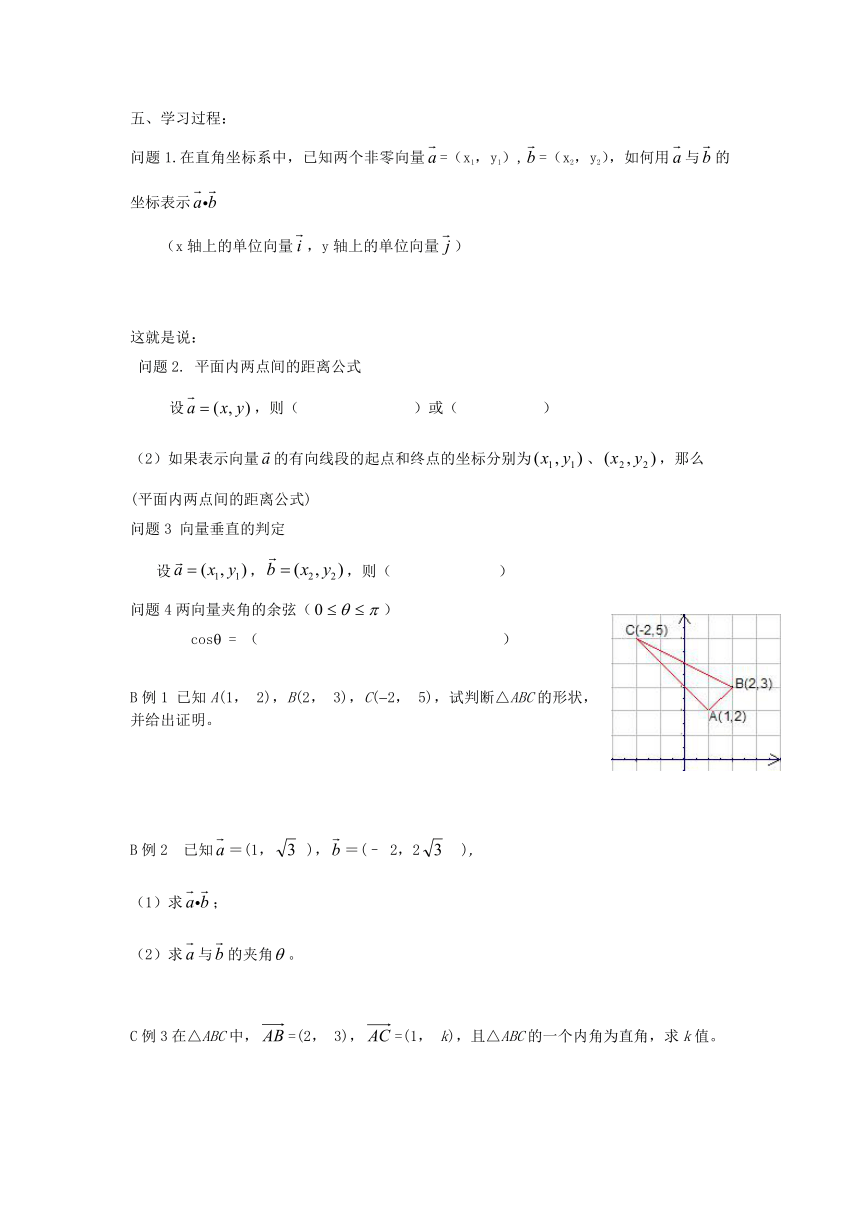
B例1 已知A(1, 2),B(2, 3),C(?2, 5),试判断△ABC的形状,并给出证明。
B例2 已知=(1, ),=(– 2,2 ),
(1)求;
(2)求与的夹角。
C例3在△ABC中,=(2, 3),=(1, k),且△ABC的一个内角为直角,求k值。
六、达标训练:
A1.若=(-4,3),=(5,6),则( )
A.23 B.57 C.63 D.83
A2.已知A(1,2),B(2,3),C(-2,5),则△ABC为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不等边三角形
A3.已知=(4,3),向量是垂直的单位向量,则等于( )
A.或? B.或
C.或? D.或
B4. =(2,3),=(-2,4),则= 。
B5.已知A(3,2),B(-1,-1),若点P(x,-)在线段AB的中垂线上,则x= 。
B6.已知A(1,0),B(3,1),C(2,0),且,,则与的夹角为 。
七、课堂小结:
1、平面向量数量积的坐标表示
2、两个向量垂直的坐标表示的充要条件
3、平面内两点间的距离公式
4、运用两个向量的数量积的坐标表示解决处理有关长度垂直的几个问题
八、课后反思:
2.4.2平面向量数量积的坐标表示、模、夹角
例1 如图,在平面直角坐标系中标出A(1, 2),B(2, 3),C(?2, 5)三点,我们发现△ABC是直角三角形
证明:∵=(1,1)=(-3,3)∴·=1×(-3)+1×3
=0
∴⊥∴△ABC是直角三角形
例2 (1)a·b=-4
(2)a与b的夹角θ为120°
例3 -或或
【达标训练】
1. A. 2. A 3. D
4. (a+b)·(a-b)= -7 .
5. x= .
6. a与b的夹角为 45° .
一、三维目标:
知识与技能:掌握平面向量数量积的坐标表示;掌握两个向量垂直的坐标条件以及能运用 两个向量的数量积的坐标表示解决有关长度、角度、垂直等几何问题。
过程与方法:通过平面向量数量积的坐标表示,进一步加深对平面向量数量积的认识,提高学生的运算速度。
情感态度与价值观:培养运算能力,创新能力,提高数学素质。
二、学习重、难点:
重点:平面向量数量积的坐标表示。
难点:平面向量数量积的坐标表示的综合运用。
三、学法指导:通过数量积的坐标表示的学习,会求夹角及两点间距离公式。
四、知识链接:
1.平面向量数量积(内积)的定义:已知两个非零向量与,它们的夹角是,则数量,叫与的数量积,记作,即有,。并规定与任何向量的数量积为0.
2.向量的数量积的几何意义:
数量积等于的长度与在方向上投影的乘积。
3.两个向量的数量积的性质:设、为两个非零向量,是与同向的单位向量。
1? ; 2?
3? 当与同向时,;当与反向时,。 特别的或4? cos? = ;5?
5.平面向量数量积的运算律
交换律:
数乘结合律:
分配律:
五、学习过程:
问题1.在直角坐标系中,已知两个非零向量=(x1,y1),=(x2,y2),如何用与的坐标表示
(x轴上的单位向量,y轴上的单位向量)
这就是说:
问题2. 平面内两点间的距离公式
设,则( )或( )
(2)如果表示向量的有向线段的起点和终点的坐标分别为、,那么
(平面内两点间的距离公式)
问题3 向量垂直的判定
设,,则( )
问题4两向量夹角的余弦()
cos? = ( )
B例1 已知A(1, 2),B(2, 3),C(?2, 5),试判断△ABC的形状,并给出证明。
B例2 已知=(1, ),=(– 2,2 ),
(1)求;
(2)求与的夹角。
C例3在△ABC中,=(2, 3),=(1, k),且△ABC的一个内角为直角,求k值。
六、达标训练:
A1.若=(-4,3),=(5,6),则( )
A.23 B.57 C.63 D.83
A2.已知A(1,2),B(2,3),C(-2,5),则△ABC为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不等边三角形
A3.已知=(4,3),向量是垂直的单位向量,则等于( )
A.或? B.或
C.或? D.或
B4. =(2,3),=(-2,4),则= 。
B5.已知A(3,2),B(-1,-1),若点P(x,-)在线段AB的中垂线上,则x= 。
B6.已知A(1,0),B(3,1),C(2,0),且,,则与的夹角为 。
七、课堂小结:
1、平面向量数量积的坐标表示
2、两个向量垂直的坐标表示的充要条件
3、平面内两点间的距离公式
4、运用两个向量的数量积的坐标表示解决处理有关长度垂直的几个问题
八、课后反思:
2.4.2平面向量数量积的坐标表示、模、夹角
例1 如图,在平面直角坐标系中标出A(1, 2),B(2, 3),C(?2, 5)三点,我们发现△ABC是直角三角形
证明:∵=(1,1)=(-3,3)∴·=1×(-3)+1×3
=0
∴⊥∴△ABC是直角三角形
例2 (1)a·b=-4
(2)a与b的夹角θ为120°
例3 -或或
【达标训练】
1. A. 2. A 3. D
4. (a+b)·(a-b)= -7 .
5. x= .
6. a与b的夹角为 45° .
