2019-2020学年数学新人教A版必修4学案:3.1.2两角和与差的正弦、余弦、正切公式Word版含答案
文档属性
| 名称 | 2019-2020学年数学新人教A版必修4学案:3.1.2两角和与差的正弦、余弦、正切公式Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 88.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览

文档简介
3.1.2两角和与差的正弦、余弦、正切公式
一、三维目标
知识与技能:能够利用两角和与差的正弦、余弦、正切公式进行简单的求值、化简和证明。
过程与方法:通过以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的过程,体验知识的迁移和转化过程。
情感态度与价值观:能运用联系的观点解决问题,认识事物之间的相互联系与相互转化,培养逻辑推理的思维能力,树立创新意识和应用意识。
二、学习重、难点
重点:两角和、差正弦和正切公式的推导过程及运用。
难点:两角和与差的正弦、余弦和正切公式的灵活运用。
三、学法指导
(1).在换元的思想指导下推导出公式;
(2).根据、及诱导公式五(或六),推导出公式;
(3).根据公式、和同角三角关系,探究公式;
(4).熟练掌握公式、、的正用、逆用、变形用。
四、知识链接
1.=
2.= ,=
3.= ,=
五、学习过程
问题1:由两角差的余弦公式,怎样得到两角和的余弦公式呢?
推导过程:
即: ()
问题2:你能根据两角和与差的余弦公式推导出两角和与差的正弦公式吗?
提示:在第一章我们用诱导公式五(或六)可以实现正弦、余弦的互化。
探究1、完成两角和与差正弦公式
=
.
即: ()
即: ()
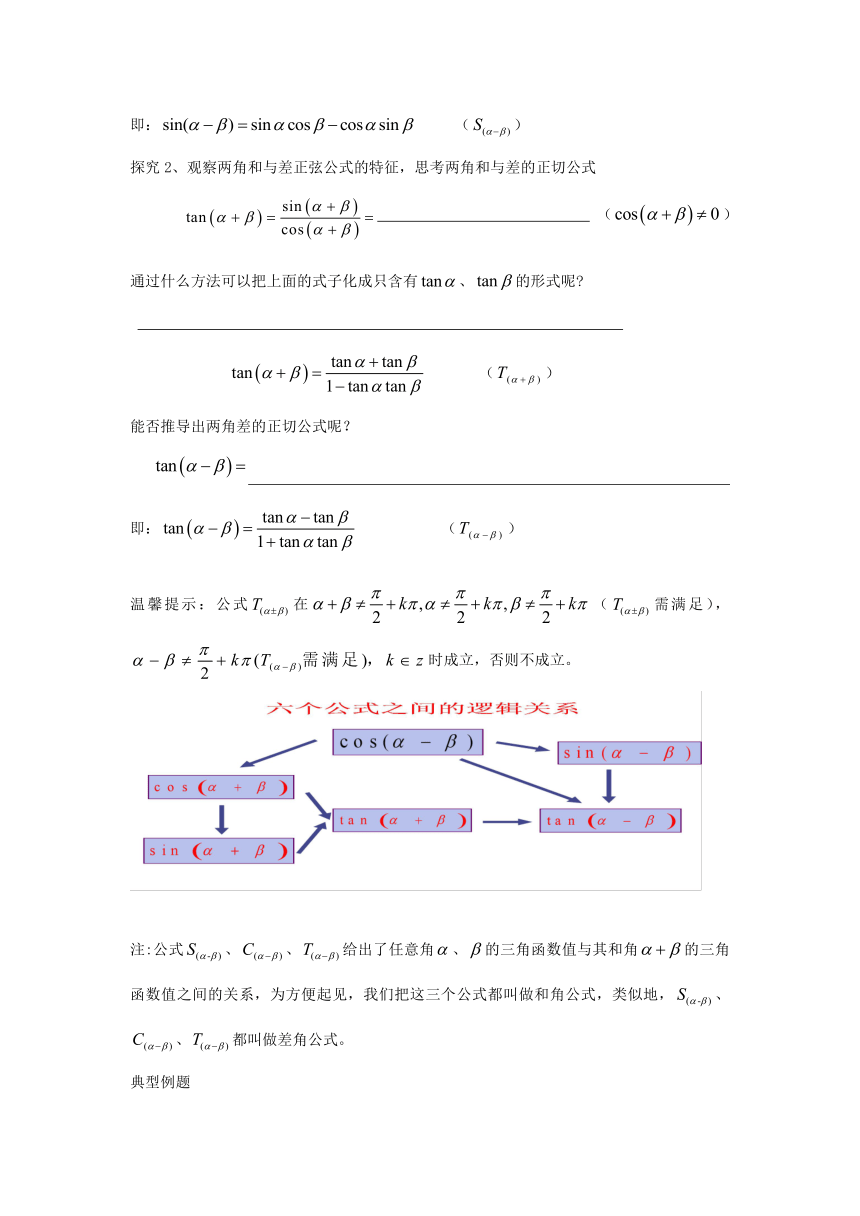
探究2、观察两角和与差正弦公式的特征,思考两角和与差的正切公式
()
通过什么方法可以把上面的式子化成只含有、的形式呢?
()
能否推导出两角差的正切公式呢?
即: ()
温馨提示:公式在(需满足),时成立,否则不成立。
注:公式、、给出了任意角、的三角函数值与其和角的三角函数值之间的关系,为方便起见,我们把这三个公式都叫做和角公式,类似地,、、都叫做差角公式。
典型例题
例1、已知是第四象限角,求的值。
思考:在本题中,,那么对任意角,此等式成立吗?若成立,你能用几种方法证明?
练习:如果,且是第四象限角,那么=________。
例2、利用和(差)角公式,求下列各式的值。
(1) (2)
六、达标训练
A1.利用和(差)角公式,求下列各式的值。
(1) (2) (3) (4)
A2.求值
(1) (2)
(3) (4)
B3.已知
A4.。
C5.已知,
C6.化简 (1) (2)
七、归纳小结:本节我们学习了两角和与差正弦、余弦和正切公式,我们要熟记公式,熟练掌握公式、、的正用、逆用、变形用。
八、课后反思:
3.1.2 两角差的正弦、正切公式《答案》
例1解:因为是第四象限角,得,
,
于是有
练习:解析:cosα=,α在第四象限,∴sinα=-,cos=-sinα=.
例2、(1)sin720cos420-cos720sin420 = sin300=
(2)
达标检测:
1.(1) (2) (3) (4)
2. (1) 1 (2) (3) 1 (4) -1
3. 4. -2 5.
6. (1) (2)
一、三维目标
知识与技能:能够利用两角和与差的正弦、余弦、正切公式进行简单的求值、化简和证明。
过程与方法:通过以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的过程,体验知识的迁移和转化过程。
情感态度与价值观:能运用联系的观点解决问题,认识事物之间的相互联系与相互转化,培养逻辑推理的思维能力,树立创新意识和应用意识。
二、学习重、难点
重点:两角和、差正弦和正切公式的推导过程及运用。
难点:两角和与差的正弦、余弦和正切公式的灵活运用。
三、学法指导
(1).在换元的思想指导下推导出公式;
(2).根据、及诱导公式五(或六),推导出公式;
(3).根据公式、和同角三角关系,探究公式;
(4).熟练掌握公式、、的正用、逆用、变形用。
四、知识链接
1.=
2.= ,=
3.= ,=
五、学习过程
问题1:由两角差的余弦公式,怎样得到两角和的余弦公式呢?
推导过程:
即: ()
问题2:你能根据两角和与差的余弦公式推导出两角和与差的正弦公式吗?
提示:在第一章我们用诱导公式五(或六)可以实现正弦、余弦的互化。
探究1、完成两角和与差正弦公式
=
.
即: ()
即: ()
探究2、观察两角和与差正弦公式的特征,思考两角和与差的正切公式
()
通过什么方法可以把上面的式子化成只含有、的形式呢?
()
能否推导出两角差的正切公式呢?
即: ()
温馨提示:公式在(需满足),时成立,否则不成立。
注:公式、、给出了任意角、的三角函数值与其和角的三角函数值之间的关系,为方便起见,我们把这三个公式都叫做和角公式,类似地,、、都叫做差角公式。
典型例题
例1、已知是第四象限角,求的值。
思考:在本题中,,那么对任意角,此等式成立吗?若成立,你能用几种方法证明?
练习:如果,且是第四象限角,那么=________。
例2、利用和(差)角公式,求下列各式的值。
(1) (2)
六、达标训练
A1.利用和(差)角公式,求下列各式的值。
(1) (2) (3) (4)
A2.求值
(1) (2)
(3) (4)
B3.已知
A4.。
C5.已知,
C6.化简 (1) (2)
七、归纳小结:本节我们学习了两角和与差正弦、余弦和正切公式,我们要熟记公式,熟练掌握公式、、的正用、逆用、变形用。
八、课后反思:
3.1.2 两角差的正弦、正切公式《答案》
例1解:因为是第四象限角,得,
,
于是有
练习:解析:cosα=,α在第四象限,∴sinα=-,cos=-sinα=.
例2、(1)sin720cos420-cos720sin420 = sin300=
(2)
达标检测:
1.(1) (2) (3) (4)
2. (1) 1 (2) (3) 1 (4) -1
3. 4. -2 5.
6. (1) (2)
