人教版七年级数学上册3.1.2等式的基本性质课件(19张 )
文档属性
| 名称 | 人教版七年级数学上册3.1.2等式的基本性质课件(19张 ) |  | |
| 格式 | rar | ||
| 文件大小 | 335.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 09:08:03 | ||
图片预览





文档简介
(共19张PPT)
一元一次方程
等式的基本性质
学习目标
1.掌握等式的性质1、性质2
2. 利用等式的性质解一元一次方程。即化成x = a(常数)形式
3. 提升观察、分析、概括能力,形成独立思考的习惯.
观察
下列四个式子有什么相同点?
用等号表示相等关系的式子,叫等式。
通常用a=b表示等式
观察
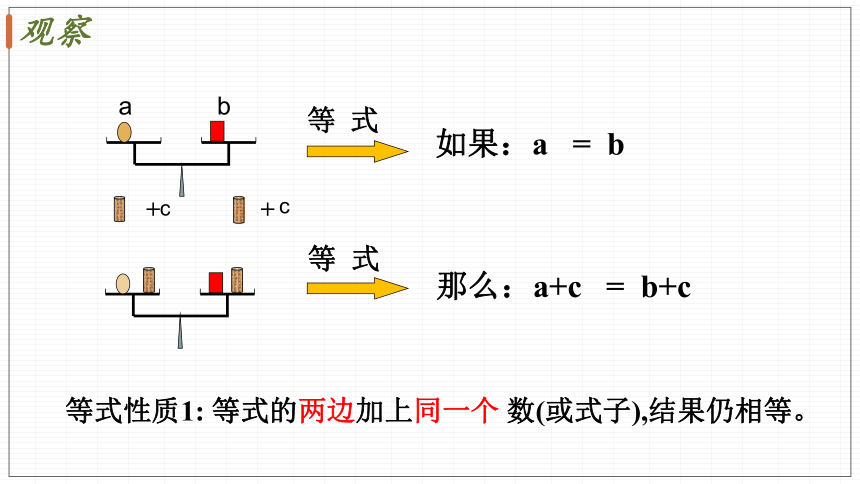
等 式
如果:a = b
+ +
等 式
那么:a+c = b+c
等式性质1: 等式的两边加上同一个 数(或式子),结果仍相等。
c
c
a
b
观察
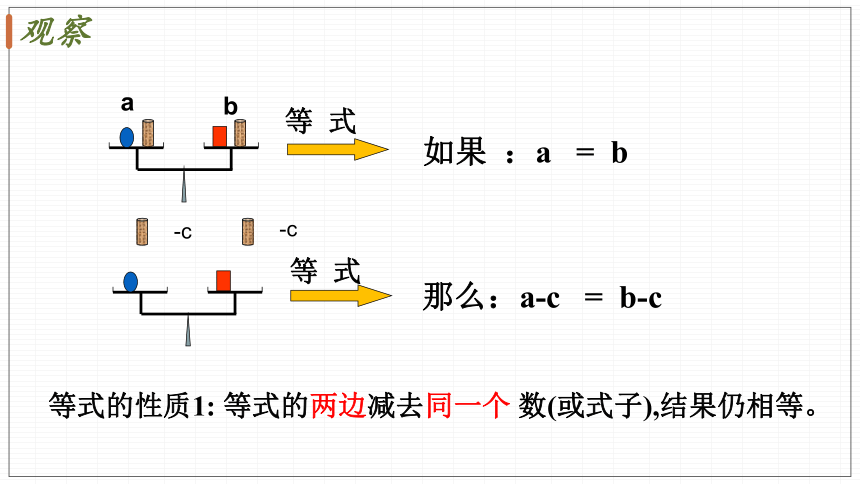
等 式
如果 :a = b
等式的性质1: 等式的两边减去同一个 数(或式子),结果仍相等。
等 式
那么:a-c = b-c
a
b
-c
-c
小结
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍是等式。
式子表示:
经过变形,化为:x = a(常数)
方程左边为一个未知数项、未知数系数是 1,右边只一个常数项。
思考1:如果x-2=3,那么x-2+2=3+2,
依据是 ,即x = ;
等式性质1
思考2:如果x + 3= -10,那么x = ;
依据是 ;
思考3:如果-2x-9= -12,那么-2x = ,
依据是 ;
思考4:如果2m+n=p+2m,那么n = ,
依据是 .
等式性质1
等式性质1
等式性质1
5
p
-3
-13
思考
例题讲解
例1、解方程: 即化为:x = a(常数)
(1)x+7=26
(2)x-31=18
练习:
解方程: (1) x - 4=29
* (2) 7x = 6x – 5
解:x+7-7=26-7
x=19
解:x-31+31=18+31
x=49
a
b
a = b
右
左
a
b
右
左
b
a
2a = 2b
观察
观察
a
b
右
左
a
a
a
a
a
a
b
b
b
b
b
b
7a = 7b
a
b
右
左
小结
等式性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
式子表示:
课堂练习
1、如果3x=5,那么3x×(-2)=5×(-2),即-6x=____;
-10
2、如果-2x=6,那么x =____;
3、已知x=3y,那么-5x=____
-6
-15y
-3
课堂练习
利用等式的性质解方程
利用等式性质2
利用等式性质1
利用等式性质2
课堂小结
等式的性质1
等式的性质2
等式两边都要参加运算,并且是作同一种运算。
注意事项
等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
等式两边不能都除以0,即0不能作除数或分母.
课堂反馈
1.已知x=y,则下列各式中:x﹣3=y﹣3;3x=3y;﹣2x=﹣2y; 中,正确的有( )
A . 1个 B. 2个 C. 3个 D.4个
C
【解析】根据“再等式的两边同时加上或减去同一个数,同时乘同一个数,或除以同一个不为零的数,等式仍然成立”得到:x﹣3=y﹣3;3x=3y;﹣2x=﹣2y均正确.而当x=y=0时,不成立。
课堂反馈
2.运用等式性质进行的变形,不正确的是( )
A .如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么2a=b+a
C. 如果a=b,那么
D.如果ax=bx,那么a=b
D
课堂反馈
【解析】两边都乘以2,得2m+6=2n.方程两边都减5,得2m+1=2n﹣5
3.由m+3=n先变形为2m+6=2n,再变形为2m+1=2n﹣5,其变形过程中所用的等式的性质及顺序是( )
A .仅用两次等式的性质1
B. 仅用两次等式的性质2
C.先用等式的性质2,再用等式的性质1
D.先用等式的性质1,再用等式的性质2
C
课堂反馈
4.填空
-2y
等式的性质2
-y
等式的性质2
变形过程:
变形过程:
两边都乘-10
两边都乘0.5
课堂反馈
6
等式的性质2
3x
等式的性质1
变形过程:
变形过程:
两边都乘1.5
两边都减去3x
一元一次方程
等式的基本性质
学习目标
1.掌握等式的性质1、性质2
2. 利用等式的性质解一元一次方程。即化成x = a(常数)形式
3. 提升观察、分析、概括能力,形成独立思考的习惯.
观察
下列四个式子有什么相同点?
用等号表示相等关系的式子,叫等式。
通常用a=b表示等式
观察
等 式
如果:a = b
+ +
等 式
那么:a+c = b+c
等式性质1: 等式的两边加上同一个 数(或式子),结果仍相等。
c
c
a
b
观察
等 式
如果 :a = b
等式的性质1: 等式的两边减去同一个 数(或式子),结果仍相等。
等 式
那么:a-c = b-c
a
b
-c
-c
小结
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍是等式。
式子表示:
经过变形,化为:x = a(常数)
方程左边为一个未知数项、未知数系数是 1,右边只一个常数项。
思考1:如果x-2=3,那么x-2+2=3+2,
依据是 ,即x = ;
等式性质1
思考2:如果x + 3= -10,那么x = ;
依据是 ;
思考3:如果-2x-9= -12,那么-2x = ,
依据是 ;
思考4:如果2m+n=p+2m,那么n = ,
依据是 .
等式性质1
等式性质1
等式性质1
5
p
-3
-13
思考
例题讲解
例1、解方程: 即化为:x = a(常数)
(1)x+7=26
(2)x-31=18
练习:
解方程: (1) x - 4=29
* (2) 7x = 6x – 5
解:x+7-7=26-7
x=19
解:x-31+31=18+31
x=49
a
b
a = b
右
左
a
b
右
左
b
a
2a = 2b
观察
观察
a
b
右
左
a
a
a
a
a
a
b
b
b
b
b
b
7a = 7b
a
b
右
左
小结
等式性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
式子表示:
课堂练习
1、如果3x=5,那么3x×(-2)=5×(-2),即-6x=____;
-10
2、如果-2x=6,那么x =____;
3、已知x=3y,那么-5x=____
-6
-15y
-3
课堂练习
利用等式的性质解方程
利用等式性质2
利用等式性质1
利用等式性质2
课堂小结
等式的性质1
等式的性质2
等式两边都要参加运算,并且是作同一种运算。
注意事项
等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
等式两边不能都除以0,即0不能作除数或分母.
课堂反馈
1.已知x=y,则下列各式中:x﹣3=y﹣3;3x=3y;﹣2x=﹣2y; 中,正确的有( )
A . 1个 B. 2个 C. 3个 D.4个
C
【解析】根据“再等式的两边同时加上或减去同一个数,同时乘同一个数,或除以同一个不为零的数,等式仍然成立”得到:x﹣3=y﹣3;3x=3y;﹣2x=﹣2y均正确.而当x=y=0时,不成立。
课堂反馈
2.运用等式性质进行的变形,不正确的是( )
A .如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么2a=b+a
C. 如果a=b,那么
D.如果ax=bx,那么a=b
D
课堂反馈
【解析】两边都乘以2,得2m+6=2n.方程两边都减5,得2m+1=2n﹣5
3.由m+3=n先变形为2m+6=2n,再变形为2m+1=2n﹣5,其变形过程中所用的等式的性质及顺序是( )
A .仅用两次等式的性质1
B. 仅用两次等式的性质2
C.先用等式的性质2,再用等式的性质1
D.先用等式的性质1,再用等式的性质2
C
课堂反馈
4.填空
-2y
等式的性质2
-y
等式的性质2
变形过程:
变形过程:
两边都乘-10
两边都乘0.5
课堂反馈
6
等式的性质2
3x
等式的性质1
变形过程:
变形过程:
两边都乘1.5
两边都减去3x
