2020年春人教版数学八年级下册第20章《数据的分析》单元测试题(A卷)(解析版)
文档属性
| 名称 | 2020年春人教版数学八年级下册第20章《数据的分析》单元测试题(A卷)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 00:16:32 | ||
图片预览


文档简介
2020年春人教版八年级下册第20章《数据的分析》单元测试题(A卷)时间:100分钟;满分:120分
班级:___________姓名:___________座号:___________成绩:___________
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)一组数据2,3,5,7,8的平均数是( )
A.2 B.3 C.4 D.5
2.(3分)一组数据4,5,7,7,8,6的中位数和众数分别是( )
A.7,7 B.7,6.5 C.6.5,7 D.5.5,7
3.(3分)为弘扬传统文化,某校初二年级举办传统文化进校园朗诵大赛,小明同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
中位数 众数 平均数 方差
9.2 9.3 9.1 0.3
A.中位数 B.众数 C.平均数 D.方差
4.(3分)某快递公司快递员张海六月第三周投放快递物品件数为:有1天是41件,有2天是35件,有4天是37件,这周里张海日平均投递物品件数为( )
A.36件 B.37件 C.38件 D.38.5件
5.(3分)下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:
甲 乙 丙 丁
平均数(分) 92 95 95 92
方差 3.6 3.6 7.4 8.1
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
6.(3分)若一组数据2,4,6,8,x的方差比另一组数据5,7,9,11,13的方差大,则 x 的值可以为( )
A.12 B.10 C.2 D.0
7.(3分)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 3.6 3.6 7.4 8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.丁 B.丙 C.乙 D.甲
8.(3分)在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17,则四个班体考成绩最稳定的是( )
A.甲班 B.乙班 C.丙班 D.丁班
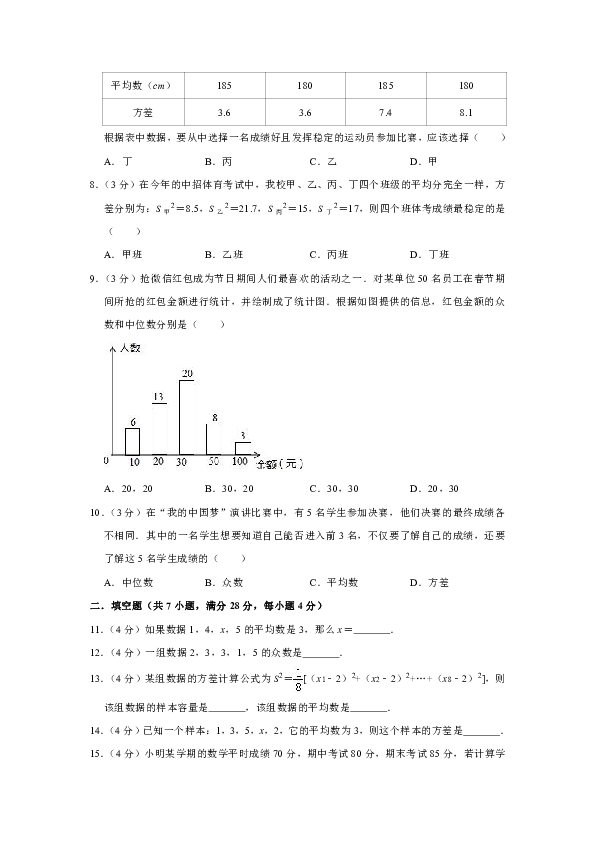
9.(3分)抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
A.20,20 B.30,20 C.30,30 D.20,30
10.(3分)在“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩的( )
A.中位数 B.众数 C.平均数 D.方差
二.填空题(共7小题,满分28分,每小题4分)
11.(4分)如果数据1,4,x,5的平均数是3,那么x= .
12.(4分)一组数据2,3,3,1,5的众数是 .
13.(4分)某组数据的方差计算公式为S2=[(x1﹣2)2+(x2﹣2)2+…+(x8﹣2)2],则该组数据的样本容量是 ,该组数据的平均数是 .
14.(4分)已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是 .
15.(4分)小明某学期的数学平时成绩70分,期中考试80分,期末考试85分,若计算学期总评成绩的方法如下:平时:期中:期末=3:3:4,则小明总评成绩是 分.
16.(4分)小明用S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .
17.(4分)甲、乙两人进行射击测试,每人20次射击成绩的平均数都是8.5环,方差分别是:S甲2=3,S乙2=2.5,则射击成绩较稳定的是 (填“甲”或“乙”).
三.解答题(共8小题,满分62分)
18.(6分)射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了五次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次
甲 10 8 9 8 10
乙 10 7 10 10 8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)经过计算:甲的五次测试成绩方差为0.8,请你求出乙的五次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
19.(6分)某品牌汽车的销售公司有营销人员14人,销售部为制定营销人员的月销售汽车定额,统计了这14人在某月的销售量如下表:
销售辆数 20 17 13 8 5 4
人 数 1 1 2 5 3 2
(1)这14位销售员该月销售某品牌汽车的平均数、众数和中位数各是多少辆?
(2)销售部经理把每位销售员每月销售汽车定额为9辆,你认为是否合理?为什么?如果不合理,请你设计一个比较合理的销售定额,并说明理由.
20.(6分)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
21.(8分)九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.
22.(8分)某校教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了表:
零花钱数额/元 5 10 15 20
学生人数 10 15 20 5
(1)求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数;
(2)你认为(1)中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适?简要说明理由.
23.(8分)某班20名同学在一次“爱心”捐款活动中,情况如下表所示
捐款(元) 0 1 2 3 4 5
人数(人) a 5 6 b 3 1
已知捐款的平均数为2.3元,求a和b的值.
24.(10分)描述一组数据的离散程度,我们可以用“极差”、“方差”、“平均差”[平均差公式为],现有甲、乙两个样本,
甲:12,13,11,15,10,16,13,14,15,11
乙:11,16,6,14,13,19,17,8,10,16
(1)分别计算甲、乙两个样本的“平均差”,并根据计算结果判断哪个样本波动较大.
(2)分别计算甲、乙两个样本的“方差”,并根据计算结果判断哪个样本波动较大.
(3)以上的两种方法判断的结果是否一致?
25.(10分)甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
第1次 第2次 第3次 第4次 第5次
甲成绩 90 40 70 40 60
乙成绩 70 50 70 a 70
甲、乙两人的数学成绩统计表
(1)a= ,= ;
(2)请完成图中表示乙成绩变化情况的折线;
(3)S甲2=360,乙成绩的方差是 ,可看出 的成绩比较稳定(填“甲”或“乙”).从平均数和方差的角度分析, 将被选中.
2020年春人教版八年级下册第20章《数据的分析》单元测试题(A卷)
解析卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)一组数据2,3,5,7,8的平均数是( )
A.2 B.3 C.4 D.5
【分析】根据平均数的定义计算.
【解答】解:数据2,3,5,7,8的平均数==5.
故选:D.
2.(3分)一组数据4,5,7,7,8,6的中位数和众数分别是( )
A.7,7 B.7,6.5 C.6.5,7 D.5.5,7
【分析】根据中位数和众数的定义分别进行解答即可.
【解答】解:把这些数从小到大排列为4,5,6,7,7,8,中位数是=6.5;
7出现了2次,出现的次数最多,则众数是7;
故选:C.
3.(3分)为弘扬传统文化,某校初二年级举办传统文化进校园朗诵大赛,小明同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
中位数 众数 平均数 方差
9.2 9.3 9.1 0.3
A.中位数 B.众数 C.平均数 D.方差
【分析】根据中位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数可得答案.
【解答】解:如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是中位数,
故选:A.
4.(3分)某快递公司快递员张海六月第三周投放快递物品件数为:有1天是41件,有2天是35件,有4天是37件,这周里张海日平均投递物品件数为( )
A.36件 B.37件 C.38件 D.38.5件
【分析】直接利用加权平均数求法进而分析得出答案.
【解答】解:由题意可得,这周里张海日平均投递物品件数为:=37(件).
故选:B.
5.(3分)下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:
甲 乙 丙 丁
平均数(分) 92 95 95 92
方差 3.6 3.6 7.4 8.1
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
【分析】方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,选出方差最小,而且平均数较大的同学参加数学比赛.
【解答】解:∵3.6<7.4<8.1,
∴甲和乙的最近几次数学考试成绩的方差最小,发挥稳定,
∵95>92,
∴乙同学最近几次数学考试成绩的平均数高,
∴要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择乙.
故选:B.
6.(3分)若一组数据2,4,6,8,x的方差比另一组数据5,7,9,11,13的方差大,则 x 的值可以为( )
A.12 B.10 C.2 D.0
【分析】利用方差定义判断即可.
【解答】解:5,7,9,11,13,这组数据的平均数为9,方差为S12=×(42+22+0+22+42)=8;
数据2,4,6,8,x的方差比这组数据方差大,则有S22>S12=8,
当x=12时,2,4,6,8,12的平均数为6.4,方差为×(4.42+2.42+0.42+1.62+5.62)=11.84,满足题意,
故选:A.
7.(3分)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 3.6 3.6 7.4 8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.丁 B.丙 C.乙 D.甲
【分析】首先比较平均数,平均数相同时选择方差较小的运动员参加.
【解答】解:∵甲和丙的平均数大于乙和丁的平均数,
∴从甲和丙中选择一人参加比赛,
∵甲的方差小于丙的方差,
∴选择甲参赛,
故选:D.
8.(3分)在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17,则四个班体考成绩最稳定的是( )
A.甲班 B.乙班 C.丙班 D.丁班
【分析】根据四个班的平均分相等结合给定的方差值,即可找出成绩最稳定的班级.
【解答】解:∵甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5、S乙2=21.7、S丙2=15、S丁2=17,且8.5<15<17<21.7,
∴甲班体考成绩最稳定.
故选:A.
9.(3分)抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
A.20,20 B.30,20 C.30,30 D.20,30
【分析】根据众数和中位数的定义,出现次数最多的那个数就是众数,把一组数据按照大小顺序排列,中间那个数或中间两个数的平均数叫中位数.
【解答】解:捐款30元的人数为20人,最多,则众数为30,
中间两个数分别为30和30,则中位数是30,
故选:C.
10.(3分)在“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩的( )
A.中位数 B.众数 C.平均数 D.方差
【分析】由于比赛取前3名进入决赛,共有5名选手参加,故应根据中位数的意义分析.
【解答】解:因为5位进入决赛者的分数肯定是5名参赛选手中最高的,
而且5个不同的分数按从小到大排序后,中位数及中位数之前的共有3个数,
故只要知道自己的分数和中位数就可以知道是否进入决赛了,
故选:A.
二.填空题(共7小题,满分28分,每小题4分)
11.(4分)如果数据1,4,x,5的平均数是3,那么x= 2 .
【分析】根据平均数的概念建立关于x的方程,然后解方程即可.
【解答】解:根据题意得,(1+4+x+5)=3,
解得x=2.
故答案为:2.
12.(4分)一组数据2,3,3,1,5的众数是 3 .
【分析】根据众数的定义求解.
【解答】解:数据2,3,3,1,5的众数为3.
故答案为3.
13.(4分)某组数据的方差计算公式为S2=[(x1﹣2)2+(x2﹣2)2+…+(x8﹣2)2],则该组数据的样本容量是 8 ,该组数据的平均数是 2 .
【分析】样本方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],其中n是这个样本的容量,是样本的平均数.利用此公式直接求解.
【解答】解:由于S2=[(x1﹣2)2+(x2﹣2)2+…+(x8﹣2)2],所以该组数据的样本容量是8,该组数据的平均数是2.
故填8,2.
14.(4分)已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是 2 .
【分析】先由平均数公式求得x的值,再由方差公式求解即可.
【解答】解:∵1,3,x,2,5,它的平均数是3,
∴(1+3+x+2+5)÷5=3,
∴x=4,
∴S2=[(1﹣3)2+(3﹣3)2+(4﹣3)2+(2﹣3)2+(5﹣3)2]=2;
∴这个样本的方差是2.
故答案为:2.
15.(4分)小明某学期的数学平时成绩70分,期中考试80分,期末考试85分,若计算学期总评成绩的方法如下:平时:期中:期末=3:3:4,则小明总评成绩是 79 分.
【分析】按3:3:4的比例算出本学期数学总评分即可.
【解答】解:本学期数学总评分=70×30%+80×30%+85×40%=79(分).
故答案为:79.
16.(4分)小明用S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= 30 .
【分析】根据计算方差的公式能够确定数据的个数和平均数,从而求得所有数据的和.
【解答】解:∵S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2],
∴平均数为3,共10个数据,
∴x1+x2+x3+…+x10=10×3=30,
故答案为:30.
17.(4分)甲、乙两人进行射击测试,每人20次射击成绩的平均数都是8.5环,方差分别是:S甲2=3,S乙2=2.5,则射击成绩较稳定的是 乙 (填“甲”或“乙”).
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【解答】解:∵S甲2=3,S乙2=2.5,
∴S甲2>S乙2,
∴乙的射击成绩较稳定.
故答案为:乙.
三.解答题(共8小题,满分62分)
18.(6分)射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了五次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次
甲 10 8 9 8 10
乙 10 7 10 10 8
(1)根据表格中的数据,计算出甲的平均成绩是 9 环,乙的平均成绩是 9 环;
(2)经过计算:甲的五次测试成绩方差为0.8,请你求出乙的五次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
【分析】(1)根据平均数的计算公式计算即可;
(2)利用方差公式计算;
(3)根据方差反映了一组数据的波动大小,方差越大,波动性越大解答即可.
【解答】解:(1)甲的平均成绩为:(10+8+9+8+10)=9,
乙的平均成绩为:(10+7+10+10+8)=9,
故答案为:9;9;
(2)乙的方差为:[(10﹣9)2+(7﹣9)2+(10﹣9)2+(10﹣9)2+(8﹣9)2]=1.6,
(3)∵0.8<1.6,
∴甲的方差小,
∴甲比较稳定,故推荐甲参加全国比赛更合适.
19.(6分)某品牌汽车的销售公司有营销人员14人,销售部为制定营销人员的月销售汽车定额,统计了这14人在某月的销售量如下表:
销售辆数 20 17 13 8 5 4
人 数 1 1 2 5 3 2
(1)这14位销售员该月销售某品牌汽车的平均数、众数和中位数各是多少辆?
(2)销售部经理把每位销售员每月销售汽车定额为9辆,你认为是否合理?为什么?如果不合理,请你设计一个比较合理的销售定额,并说明理由.
【分析】(1)用加权平均数的求法求得其平均数,出现最多的数据为众数,排序后位于中间位置的数即为中位数.
【解答】解:(1)平均数:=9;
众数:8;中位数:8
(2)不合理,因为达到指标的人数太少.应选8比较合理,因为中位数和众数都是8,能代表一般水平.
20.(6分)随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 16 ,众数是 17 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
【分析】(1)将数据按照大小顺序重新排列,计算出中间两个数的平均数即是中位数,出现次数最多的即为众数;
(2)根据平均数的概念,将所有数的和除以10即可;
(3)用样本平均数估算总体的平均数.
【解答】解:(1)按照大小顺序重新排列后,第5、第6个数分别是15和17,所以中位数是(15+17)÷2=16,17出现3次最多,所以众数是17,
故答案是16,17;
(2)=14,
答:这10位居民一周内使用共享单车的平均次数是14次;
(3)200×14=2800(次)
答:该小区居民一周内使用共享单车的总次数为2800次.
21.(8分)九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 9.5 分,乙队成绩的众数是 10 分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 乙 队.
【分析】(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
【解答】解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:(10×4+8×2+7+9×3)=9,
则方差是:[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
22.(8分)某校教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了表:
零花钱数额/元 5 10 15 20
学生人数 10 15 20 5
(1)求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数;
(2)你认为(1)中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适?简要说明理由.
【分析】(1)利用平均数、中位数及众数的定义求解;
(2)在平均数,众数两数中,平均数受到极端值的影响较大,所以众数更能反映家庭年收入的一般水平.
【解答】解:(1)平均数是=12元,
数据15出现次数最多,故众数是15元,中位数是=12.5元;
(2)用众数代表这50名学生一周零花钱数额的一般水平较为合适,因为15元出现次数最多,所以能代表一周零花钱的一般水平
23.(8分)某班20名同学在一次“爱心”捐款活动中,情况如下表所示
捐款(元) 0 1 2 3 4 5
人数(人) a 5 6 b 3 1
已知捐款的平均数为2.3元,求a和b的值.
【分析】首先利用其加权平均数求得b的值,然后用学生总数减去其他人数即可求得a的值.
【解答】解:∵
∴b=4
∴a=20﹣5﹣6﹣4﹣3﹣1=1
答:a的值为1,b的值为4.
24.(10分)描述一组数据的离散程度,我们可以用“极差”、“方差”、“平均差”[平均差公式为],现有甲、乙两个样本,
甲:12,13,11,15,10,16,13,14,15,11
乙:11,16,6,14,13,19,17,8,10,16
(1)分别计算甲、乙两个样本的“平均差”,并根据计算结果判断哪个样本波动较大.
(2)分别计算甲、乙两个样本的“方差”,并根据计算结果判断哪个样本波动较大.
(3)以上的两种方法判断的结果是否一致?
【分析】先由平均数的公式计算出x的值,再根据标准差与方差的公式计算.
【解答】解:(1)甲组的平均数为(12+13+11+15+10+16+13+14+15+11)÷10=13,
T甲=(1+0+2+2+3+3+0+1+2+2)÷10=1.6
乙组的平均数为(11+16+6+14+13+19+17+8+10+16)÷10=13,
T乙=(2+3+7+1+0+6+4+5+3+3)÷10=3.4.
3.4>1.6,所以乙样本波动大;
(2)S2甲=[(12﹣13)2+(13﹣13)2+(11﹣13)2+(15﹣13)2+(10﹣13)2+(16﹣13)2+(13﹣13)2+(14﹣13)2+(15﹣13)2+(11﹣13)2]÷10=3.6,
S2乙=[(11﹣13)2+(16﹣13)2+(6﹣13)2+(14﹣13)2+(13﹣13)2+(19﹣13)2+(17﹣13)2+(8﹣13)2+(10﹣13)2+(16﹣13)2]÷10=15.8,
15.8>3.6,所以乙样本波动大.
(3)结果一致.
25.(10分)甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
第1次 第2次 第3次 第4次 第5次
甲成绩 90 40 70 40 60
乙成绩 70 50 70 a 70
甲、乙两人的数学成绩统计表
(1)a= 40 ,= 60 ;
(2)请完成图中表示乙成绩变化情况的折线;
(3)S甲2=360,乙成绩的方差是 160 ,可看出 乙 的成绩比较稳定(填“甲”或“乙”).从平均数和方差的角度分析, 乙 将被选中.
【分析】(1)根据题意和平均数的计算公式计算即可;
(2)根据求出的a的值,完成图中表示乙成绩变化情况的折线;
(3)根据方差的计算公式计算,根据方差的性质进行判断即可.
【解答】解:(1)∵他们的5次总成绩相同,
∴90+40+70+40+60=70+50+70+a+70,
解得a=40,
(70+50+70+40+70)=60,
故答案为:40;60;
(2)如图所示:
(3)S2乙=[(70﹣60)2+(50﹣60)2+(70﹣60)2+(40﹣60)2+(70﹣60)2]=160.
∵S2乙<S甲2,
∴乙的成绩稳定,
从平均数和方差的角度分析,乙将被选中,
故答案为:160;乙;乙.
