2020年北师大版数学下册九年级《第3章 圆》单元测试卷(解析版)
文档属性
| 名称 | 2020年北师大版数学下册九年级《第3章 圆》单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 645.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 00:00:00 | ||
图片预览

文档简介
2020年北师大版数学下册九年级《第3章 圆》单元测试卷
一.选择题(共12小题)
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
2.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2 B.4cm C. D.
3.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
A.6.5米 B.9米 C.13米 D.15米
4.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )
A.(﹣1,) B.(0,) C.(,0) D.(1,)
5.AB是⊙O的弦,∠AOB=80°,则弦AB所对的圆周角是( )
A.40° B.140°或40° C.20° D.20°或160°
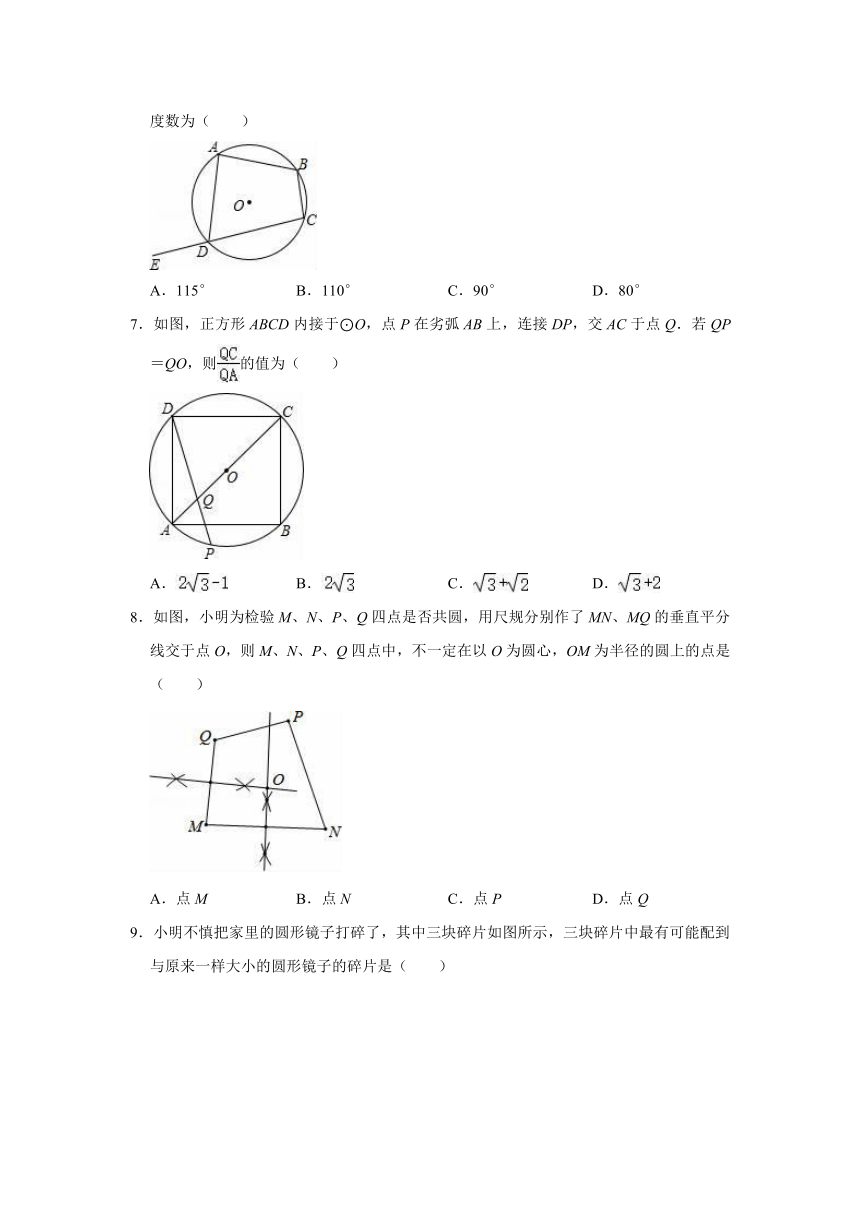
6.如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
A.115° B.110° C.90° D.80°
7.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
8.如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M B.点N C.点P D.点Q
9.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.均不可能
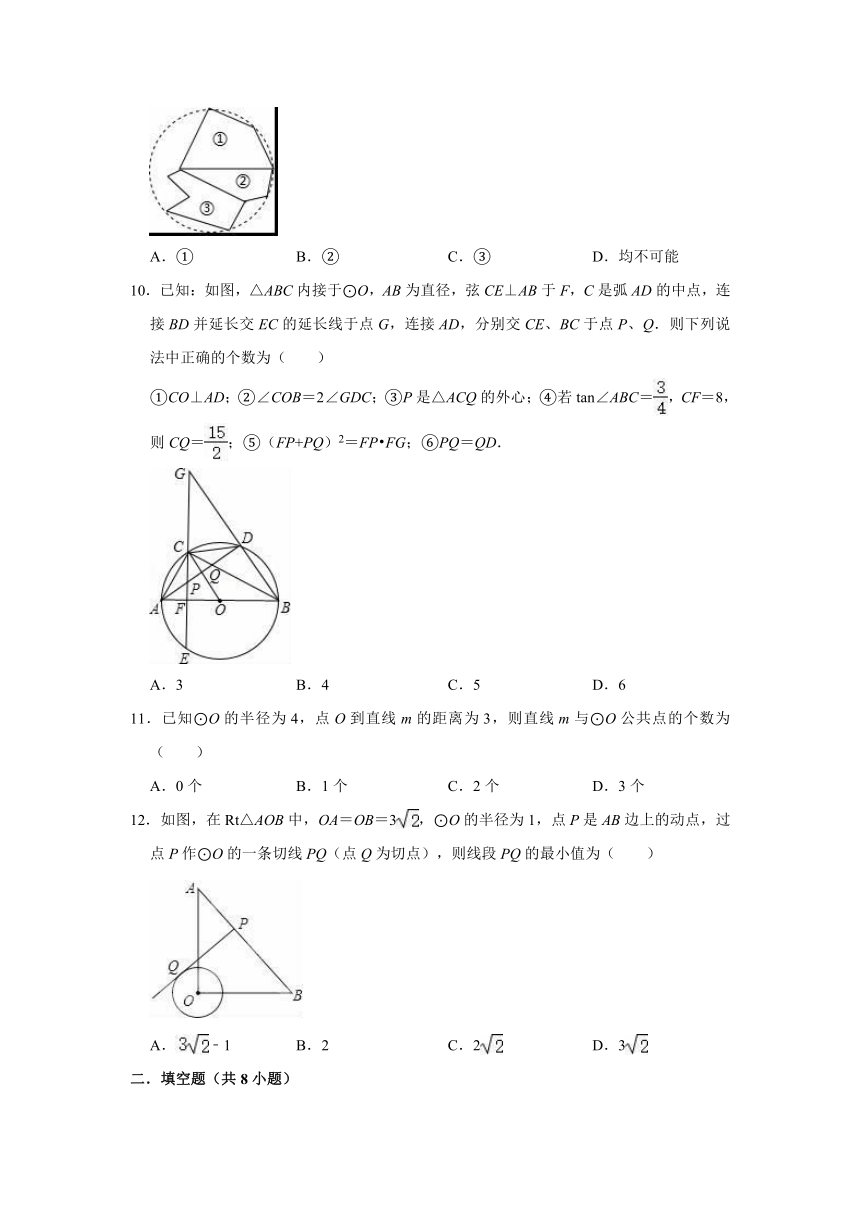
10.已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q.则下列说法中正确的个数为( )
①CO⊥AD;②∠COB=2∠GDC;③P是△ACQ的外心;④若tan∠ABC=,CF=8,则CQ=;⑤(FP+PQ)2=FP?FG;⑥PQ=QD.
A.3 B.4 C.5 D.6
11.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
12.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
二.填空题(共8小题)
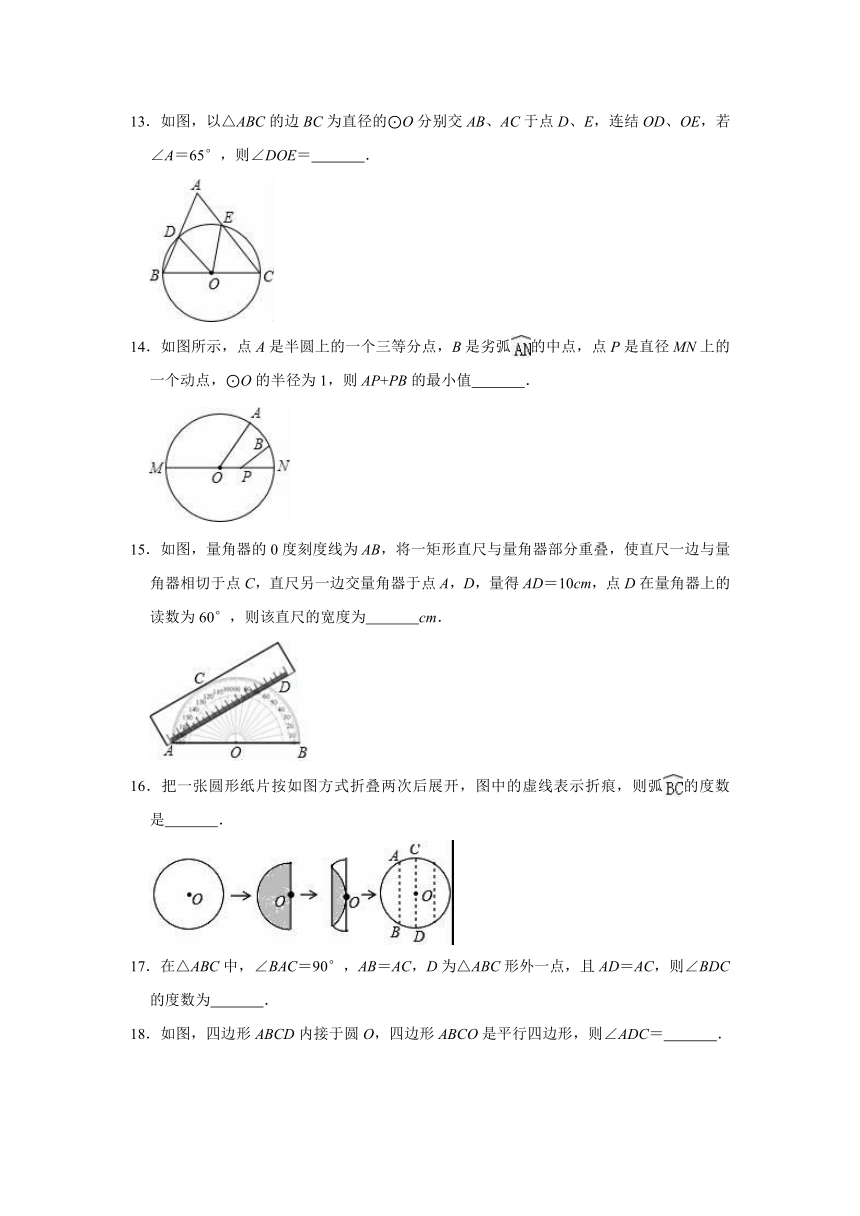
13.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= .
14.如图所示,点A是半圆上的一个三等分点,B是劣弧的中点,点P是直径MN上的一个动点,⊙O的半径为1,则AP+PB的最小值 .
15.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
16.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则弧的度数是 .
17.在△ABC中,∠BAC=90°,AB=AC,D为△ABC形外一点,且AD=AC,则∠BDC的度数为 .
18.如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC= .
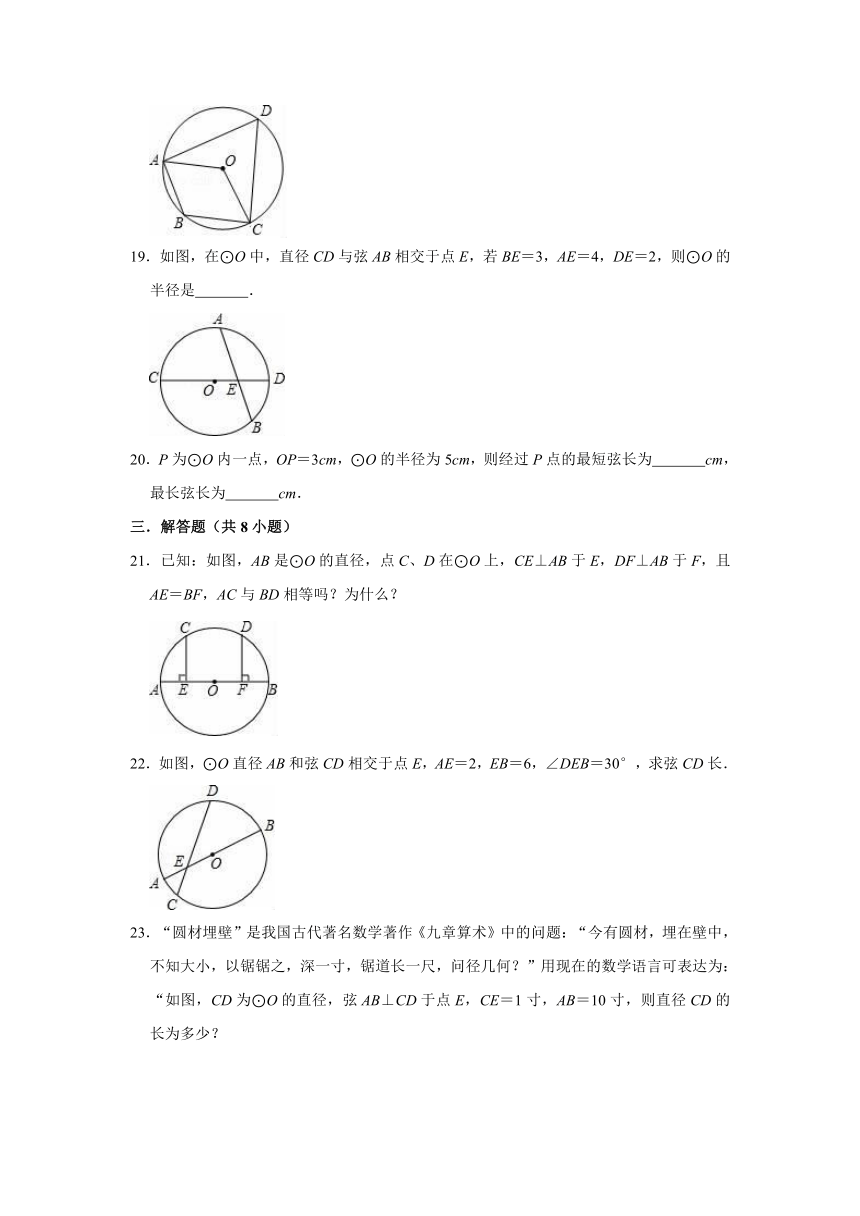
19.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 .
20.P为⊙O内一点,OP=3cm,⊙O的半径为5cm,则经过P点的最短弦长为 cm,最长弦长为 cm.
三.解答题(共8小题)
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
22.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
23.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?
24.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交于AB于C、D两点,求证:AC=BD.
25.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.
(1)求直径AB的长;
(2)求阴影部分的面积(结果保留π).
26.如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD?DC=PA?BC.
27.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
28.已知直角三角形ABC和ADC有公共斜边AC,M、N分别是AC,BD中点,且M、N不重合.
(1)线段MN与BD是否垂直?请说明理由;
(2)若∠BAC=30°,∠CAD=45°,AC=4,求MN的长.
2020年北师大版数学下册九年级《第3章 圆》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
【分析】根据等弧的定义对A进行判断;根据垂径定理对B进行判断;根据圆心角、弧、弦的关系对C进行判断;根据圆的对称性对D进行判断.
【解答】解:A、能完全重合的两条弧是等弧,所以A选项错误;
B、平分弦(非直径)的直径垂直于弦,所以B选项错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以C选项错误;
D、经过圆心的每一条直线都是圆的对称轴,所以D选项正确.
故选:D.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了垂径定理和圆心角、弧、弦的关系.
2.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2 B.4cm C. D.
【分析】连接AO,过O作OD⊥AB,交于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.
【解答】解:如图所示,
连接AO,过O作OD⊥AB,交于点D,交弦AB于点E,
∵折叠后恰好经过圆心,
∴OE=DE,
∵⊙O的半径为4,
∴OE=OD=×4=2,
∵OD⊥AB,
∴AE=AB,
在Rt△AOE中,
AE===2.
∴AB=2AE=4.
故选:B.
【点评】本题考查的是垂径定理在实际生活中的运用及翻折变换的性质,根据题意画出图形,作出辅助线利用数形结合解答.
3.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
A.6.5米 B.9米 C.13米 D.15米
【分析】根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O.
连接OA.根据垂径定理和勾股定理求解.
【解答】解:根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O
连接OA.根据垂径定理,得AD=6
设圆的半径是r,根据勾股定理,得r2=36+(r﹣4)2,解得r=6.5
故选:A.
【点评】此题综合运用了勾股定理以及垂径定理.注意构造由半径、半弦、弦心距组成的直角三角形进行有关的计算.
4.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )
A.(﹣1,) B.(0,) C.(,0) D.(1,)
【分析】连接OQ、OP,求出∠POQ的度数,得出等边三角形POQ,得出PQ=OQ=OP=2,∠OPQ=∠OQP=60°,求出∠AOQ度数,根据三角形的内角和定理求出∠QAO,求出AQ、OA,即可得出答案.
【解答】解:连接OQ、PO,
则∠POQ=120°﹣60°=60,
∵PO=OQ,
∴△POQ是等边三角形,
∴PQ=OP=OQ=×4cm=2cm,∠OPQ=∠OQP=60°,
∵∠AOQ=90°﹣60°=30°,
∴∠QAO=180°﹣60°﹣30°=90°,
∴AQ=OQ=1cm,
∵在Rt△AOQ中,由勾股定理得:OA==,
∴A的坐标是(0,),
故选B.
方法二:由于是选择题,只有B选项在y轴上,
故选:B.
【点评】本题考查了圆心角、弧、弦之间的关系,三角形的内角和定理,勾股定理,等边三角形的性质和判定等知识点,解此题的关键是构造三角形后求出OA的长,主要考查学生分析问题和解决问题的能力.
5.AB是⊙O的弦,∠AOB=80°,则弦AB所对的圆周角是( )
A.40° B.140°或40° C.20° D.20°或160°
【分析】此题要分两种情况:当圆周角的顶点在优弧上时;当圆周角的顶点在劣弧上时;通过分析,从而得到答案.
【解答】解:当圆周角的顶点在优弧上时,根据圆周角定理,得圆周角:
∠ACB=∠AOB=×80°=40°;
当圆周角的顶点在劣弧上时,根据圆内接四边形的性质,得此圆周角:
∠ADB=180°﹣∠ACB=180°﹣40°=140°;
所以弦AB所对的圆周角是40°或140°.
故选:B.
【点评】注意:弦所对的圆周角有两种情况,且两种情况的角是互补的关系.
6.如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
A.115° B.110° C.90° D.80°
【分析】由四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,根据圆的内接四边形的性质,即可求得∠ADC的度数,继而求得答案.
【解答】解:∵四边形ABCD内接于圆O,∠B=110°,
∴∠ADC=180°﹣∠B=70°,
∴∠ADE=180°﹣∠ADC=110°.
故选:B.
【点评】此题考查了圆的内接多边形的性质.注意圆的内接四边形的对角互补.
7.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
【分析】设⊙O的半径为r,QO=m,则QP=m,QC=r+m,QA=r﹣m.利用相交弦定理,求出m与r的关系,即用r表示出m,即可表示出所求比值.
【解答】解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA?QC=QP?QD.
即(r﹣m)(r+m)=m?QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选:D.
【点评】本题考查了相交弦定理,即“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”.熟记并灵活应用定理是解题的关键.
8.如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M B.点N C.点P D.点Q
【分析】连接OM,ON,OQ,OP,由线段垂直平分线的性质可得出OM=ON=OQ,据此可得出结论.
【解答】解:连接OM,ON,OQ,OP,
∵MN、MQ的垂直平分线交于点O,
∴OM=ON=OQ,
∴M、N、Q再以点O为圆心的圆上,OP与ON的大小不能确定,
∴点P不一定在圆上.
故选:C.
【点评】本题考查的是点与圆的位置关系及线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.
9.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.均不可能
【分析】要确定圆的大小需知道其半径.根据垂径定理知第①块可确定半径的大小.
【解答】解:第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
【点评】本题考查了垂径定理的应用,确定圆的条件,解题的关键是熟练掌握:圆上任意两弦的垂直平分线的交点即为该圆的圆心.
10.已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q.则下列说法中正确的个数为( )
①CO⊥AD;②∠COB=2∠GDC;③P是△ACQ的外心;④若tan∠ABC=,CF=8,则CQ=;⑤(FP+PQ)2=FP?FG;⑥PQ=QD.
A.3 B.4 C.5 D.6
【分析】①由于C是弧AD的中点,根据垂径定理即可证明CO⊥AD;
②根据圆内接四边形的性质可得∠GDC=∠BAC,根据圆周角等量可得∠COB=2∠BAC,等量代换可得∠COB=2∠GDC;
③由于AB是⊙O的直径,则∠ACB=90°,只需证明P是Rt△ACQ斜边AQ的中点即可;由垂径定理易知弧AC=弧AE,而C是弧AD的中点,那么弧CD=弧AE,即∠PAC=∠PCA,根据等角的余角相等,还可得到∠AQC=∠PCQ,由此可证得AP=PC=PQ,即P是△ACQ的外心;
④由③的相等弧可知:∠ABC=∠ACE=∠CAQ,那么它们的正切值也相等;在Rt△CAF中,根据CF的长及∠ACF的正切值,通过解直角三角形可求得AC的长,进而可在Rt△CAQ中,根据∠CAQ的正切值求出CQ的长;
⑤由③知:PQ=CP,则所求的乘积式可化为:CF2=FP?FG;在Rt△ACB中,由射影定理得:CF2=AF?FB,因此只需证明AF?FB=FG?FP即可,将上式化成比例式,证线段所在的三角形相似即可,即证Rt△AFP∽Rt△GFB;
⑥根据题目已知无法证明PQ=QD,依此即可作出判断.
【解答】①证明∵C是弧AD的中点,
∴∴弧AC=弧CD,
∴CO⊥AD;
②∵四边形ABDC是圆内接四边形,
∴∠GDC=∠BAC,
∵∠COB=2∠BAC,
∴∠COB=2∠GDC;
③证明:∵C是弧AD的中点,
∴弧AC=弧CD,
∴∠CAD=∠ABC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠CAD+∠AQC=90°
又∵CE⊥AB,
∴∠ABC+∠PCQ=90°
∴∠AQC=∠PCQ
∴在△PCQ中,PC=PQ,
∵CE⊥直径AB,
∴弧AC=弧AE,
∴弧AE=弧CD,
∴∠CAD=∠ACE.
∴在△APC中,有PA=PC,
∴PA=PC=PQ
∴P是△ACQ的外心.
④解:∵CE⊥直径AB于F,
∴在Rt△BCF中,由tan∠ABC==,CF=8,
得BF=.
∴由勾股定理,得BC==,
∵AB是⊙O的直径,
∴在Rt△ACB中,由tan∠ABC==,BC=,
∴AC=10,
易知Rt△ACB∽Rt△QCA,
∴AC2=CQ?BC,
∴CQ==;
⑤证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
又∵CF⊥AB,
∴∠ABG+∠G=90°,
∴∠DAB=∠G;
∴Rt△AFP∽Rt△GFB,
∴=,即AF?BF=FP?FG
易知Rt△ACF∽Rt△CBF,
∴CF2=AF?BF(或由射影定理得)
∴FC2=PF?FG,
由③,知PC=PQ,
∴FP+PQ=FP+PC=FC
∴(FP+PQ)2=FP?FG;
⑥由题目条件无法得到PQ=QD.
故选:C.
【点评】此题考查了三角形的外接圆与外心,圆周角定理,相似三角形的判定与性质,涉及的知识点有:圆心角、弧的关系,垂径定理,圆内接四边形的性质,圆周角定理,三角形的外接圆与外心,勾股定理以及相似三角形的判定和性质等知识,综合性较强,有一定的难度.
11.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
【分析】根据直线和圆的位置关系判断方法,可得结论.
【解答】解:∵d=3<半径=4
∴直线与圆相交
∴直线m与⊙O公共点的个数为2个
故选:C.
【点评】本题考查了直线与圆的位置关系,掌握直线和圆的位置关系判断方法:设⊙O的半径为r,圆心O到直线l的距离为d.①直线l和⊙O相交?d<r②直线l和⊙O相切?d=r,③直线l和⊙O相离?d>r.
12.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
【分析】首先连接OP、OQ,根据勾股定理知PQ2=OP2﹣OQ2,可得当OP⊥AB时,即线段PQ最短,然后由勾股定理即可求得答案.
【解答】解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2﹣OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3,
∴AB=OA=6,
∴OP==3,
∴PQ==2.
故选:C.
【点评】本题考查了切线的性质、等腰直角三角形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意得到当PO⊥AB时,线段PQ最短是关键.
二.填空题(共8小题)
13.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= 50° .
【分析】如图,连接BE.由圆周角定理和三角形内角和定理求得∠ABE=25°,再由“同弧所对的圆周角是所对的圆心角的一半”进行答题.
【解答】解:如图,连接BE.
∵BC为⊙O的直径,
∴∠CEB=∠AEB=90°,
∵∠A=65°,
∴∠ABE=25°,
∴∠DOE=2∠ABE=50°,(圆周角定理)
故答案为:50°.
【点评】本题考查了圆的认识及三角形的内角和定理等知识,难度不大.
14.如图所示,点A是半圆上的一个三等分点,B是劣弧的中点,点P是直径MN上的一个动点,⊙O的半径为1,则AP+PB的最小值 .
【分析】本题是要在MN上找一点P,使PA+PB的值最小,设A′是A关于MN的对称点,连接A′B,与MN的交点即为点P.此时PA+PB=A′B是最小值,可证△OA′B是等腰直角三角形,从而得出结果.
【解答】解:作点A关于MN的对称点A′,连接A′B,交MN于点P,连接OA′,OA,OB,PA,AA′.
∵点A与A′关于MN对称,点A是半圆上的一个三等分点,
∴∠A′ON=∠AON=60°,PA=PA′,
∵点B是弧AN的中点,
∴∠BON=30°,
∴∠A′OB=∠A′ON+∠BON=90°,
又∵OA=OA′=1,
∴A′B=.
∴PA+PB=PA′+PB=A′B=.
故答案为:.
【点评】本题结合图形的性质,考查轴对称﹣﹣最短路线问题.其中求出∠BOA′的度数是解题的关键.
15.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
【分析】连接OC,利用垂径定理解答即可.
【解答】解:连接OC,
∵直尺一边与量角器相切于点C,
∴OC⊥AD,
∵AD=10,∠DOB=60°,
∴∠DAO=30°,
∴OE=,OA=,
∴CE=OC﹣OE=OA﹣OE=,
故答案为:
【点评】此题考查垂径定理,关键是利用垂径定理解答.
16.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则弧的度数是 150° .
【分析】作辅助线,证明△AGO是等边三角形,则∠AOG=60°,同理∠BOG=60°,所以∠BOC=90°+60°=150°,根据圆心角的度数等于弧的度数可以得出结论.
【解答】解:如图,
过O作OG⊥AB,交⊙O于G,交AB于H,连接AG、AO,
由折叠得:GH=OH,
∴AG=AO,
∵AO=OG,
∴AO=OG=AG,
∴△AGO是等边三角形,
∴∠AOG=60°,
同理∠BOG=60°,
∴∠BOC=90°+60°=150°,
则弧的度数是150°;
故答案为:150°.
【点评】本题考查了圆心角、弧、弦的性质、垂径定理、等腰三角形的三线合一的性质、翻折变换,明确翻折前后的边相等,熟练掌握垂径定理、等腰三角形的三线合一的性质是关键.
17.在△ABC中,∠BAC=90°,AB=AC,D为△ABC形外一点,且AD=AC,则∠BDC的度数为 45°或135° .
【分析】首先根据题意画出图形,由AB=AC,AD=AC,可得点B,C,D在以A为圆心,AB为半径的圆上,然后由圆周角定理与圆的内接四边形的性质,求得∠BDC的度数.
【解答】解:如图,∵AB=AC,AD=AC,
∴点B,C,D在以A为圆心,AB为半径的圆上,
∴∠BDC=∠BAC=×90°=45°,
∠BD′C=180°﹣∠BDC=135°.
∴∠BDC的度数为45°或135°.
故答案为:45°或135°.
【点评】此题考查了圆周角定理以及圆的内接四边形的性质.注意根据题意画出图形,得到点B,C,D在以A为圆心,AB为半径的圆上是关键.
18.如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC= 60° .
【分析】设∠ADC的度数=α,∠ABC的度数=β,由题意可得,求出β即可解决问题.
【解答】解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠AOC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故答案为:60°.
【点评】该题主要考查了圆周角定理及其应用问题;应牢固掌握该定理并能灵活运用.
19.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 4 .
【分析】利用相交弦定理,可以求出CE的长,从而知道CD的长,就可求出⊙O的半径.
【解答】解:根据相交弦定理,AE?BE=CE?DE,
又∵BE=3,AE=4,DE=2,
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4.
故此题应该填4.
【点评】此题考查了相交弦定理,先求出直径,再得出半径.
20.P为⊙O内一点,OP=3cm,⊙O的半径为5cm,则经过P点的最短弦长为 8 cm,最长弦长为 10 cm.
【分析】当弦与OP垂直时,弦最短,过P点经过圆心的弦最长.
【解答】解:当弦与OP垂直时,弦最短,最短弦为8cm,
过P点经过圆心的弦最长为直径,最长弦为10cm.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
三.解答题(共8小题)
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
【分析】连结OC、OD,由OA=OB,AE=BF,得到OE=OF,由CE⊥AB,DF⊥AB得到∠OEC=∠OFD=90°,再根据“HL”可判断Rt△OEC≌Rt△OFD,则∠COE=∠DOF,所以AC弧=BD弧,AC=BD.
【解答】解:AC与BD相等.理由如下:
连结OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了直角三角形全等的判定与性质.
22.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
【分析】过O作OF垂直于CD,连接OD,利用垂径定理得到F为CD的中点,由AE+EB求出直径AB的长,进而确定出半径OA与OD的长,由OA﹣AE求出OE的长,在直角三角形OEF中,利用30°所对的直角边等于斜边的一半求出OF的长,在直角三角形ODF中,利用勾股定理求出DF的长,由CD=2DF即可求出CD的长.
【解答】解:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA﹣AE=4﹣2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,
则CD=2DF=2.
【点评】此题考查了垂径定理,勾股定理,以及含30°直角三角形的性质,利用了转化的思想,熟练掌握定理是解本题的关键.
23.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?
【分析】连接OA构成直角三角形,先根据垂径定理,由DE垂直AB得到点E为AB的中点,由AB=10可求出AE的长,再设出圆的半径OA为x,表示出OE,根据勾股定理建立关于x的方程,求出方程的解即可得到x的值,即为圆的半径,把求出的半径代入即可得到答案.
【解答】解:连接OA,∵AB⊥CD,且AB=10,
∴AE=BE=5,
设圆O的半径OA的长为x,则OC=OD=x
∵CE=1,
∴OE=x﹣1,
在直角三角形AOE中,根据勾股定理得:
x2﹣(x﹣1)2=52,化简得:x2﹣x2+2x﹣1=25,
即2x=26,
解得:x=13
所以CD=26(寸).
【点评】此题考查了学生对垂径定理的运用与掌握,注意利用圆的半径,弦的一半及弦心距所构成的直角三角形来解决实际问题,做此类题时要多观察,多分析,才能发现线段之间的联系.
24.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交于AB于C、D两点,求证:AC=BD.
【分析】连接OA、OB,根据半径相等得到∠A=∠B,根据等弧所对的圆周角相等得到∠AOC=∠BOD,根据三角形全等的判定定理证明△AOC≌△BOD,根据全等三角形的性质证明结论.
【解答】证明:连接OA、OB,
∵OA=OB,
∴∠A=∠B,
∵=,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD.
【点评】本题考查的是圆心角、弧、弦的关系以及三角形全等的判定和性质,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等是解题的关键.
25.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.
(1)求直径AB的长;
(2)求阴影部分的面积(结果保留π).
【分析】(1)根据直径所对的圆周角是直角推知∠ACB=90°,然后在直角三角形ABC中利用边角关系、勾股定理来求直径AB的长度;
(2)连接OD.利用(1)中求得AB=4可以推知OA=OD=2;然后由角平分线的性质求得∠AOD=90°;最后由扇形的面积公式、三角形的面积公式可以求得
阴影部分的面积=S扇形△AOD﹣S△AOD.
【解答】解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,…(1分)
∵∠B=30°,
∴AB=2AC,…(3分)
∵AB2=AC2+BC2,
∴AB2=AB2+62,…(5分)
∴AB=4. …(6分)
(2)连接OD.
∵AB=4,∴OA=OD=2,…(8分)
∵CD平分∠ACB,∠ACB=90°,
∴∠ACD=45°,
∴∠AOD=2∠ACD=90°,…(9分)
∴S△AOD=OA?OD=?2?2=6,…(10分)
∴S扇形△AOD=?π?OD2=?π?(2)2=3π,…(11分)
∴阴影部分的面积=S扇形△AOD﹣S△AOD=3π﹣6. …(12分)
【点评】本题综合考查了圆周角定理、含30度角的直角三角形以及扇形面积公式.解答(2)题时,采用了“数形结合”的数学思想.
26.如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD?DC=PA?BC.
【分析】要证AD?DC=PA?BC,需证△PAD∽△DCB;由DP∥AC,可得∠ADP=∠DAC=∠DBC;由于∠DAP是圆内接四边形ABCD的一个外角,故有∠DAP=∠DCB;从而△PAD∽△DCB成立,由此得证.
【解答】证明:如图,连接AC,连接BD.
∵DP∥AC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB.
∴△PAD∽△DCB.
得PA:DC=AD:BC,
即AD?DC=PA?BC.
【点评】本题考查了平行线的性质,圆周角定理,相似三角形的判定和性质等知识.
27.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 (2,0) ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
【分析】(1)由网格容易得出AB的垂直平分线和BC的垂直平分线,它们的交点即为点M;
(2)根据图形即可得出点M的坐标
(3)用两点间距离公式求出圆的半径和线段DM的长,当DM小于圆的半径时点D在圆内.
【解答】解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).
故答案为(2,0);
(3)圆的半径AM==2.
线段MD==<2,
所以点D在⊙M内.
【点评】本题考查的是点与圆的位置关系,坐标与图形性质以及垂径定理,利用网格结构得到圆心M的坐标是解题的关键.
28.已知直角三角形ABC和ADC有公共斜边AC,M、N分别是AC,BD中点,且M、N不重合.
(1)线段MN与BD是否垂直?请说明理由;
(2)若∠BAC=30°,∠CAD=45°,AC=4,求MN的长.
【分析】(1)根据题意画出图形,再作出辅助线构成等腰三角形,利用等腰三角形的性质进行证明;
(2)注意要分二种情况讨论:即B、D在AC两侧和B、D在AC同侧.
【解答】解:(1)线段MN与BD垂直.
连接MB与MD,由直角三角形斜边上的中线等于斜边长的一半,可以知道
MB=,MD=,所以MB=MD.
三角形MBD中,N是底边上的中点,等腰三角形的性质可以说明:
MN垂直BD.
(2)如图一:连接BM、MD,延长DM,过B作DM延长线的垂线段BE,
∵M是AC的中点,
∴MD⊥AC,△BCM是等边三角形,
∴在Rt△BEM中,∠EMB=30°,
∵AC=4,∴BM=2,
∴BE=1,EM=,MD=2,
从而可知
BD==2
∴BN=.
由Rt△BMN可得:
MN==.
如图二:连接BM、MD,延长AD,过B作垂线段BE,
∵M、N分别是AC,BD中点,
∴MD=AC,MBAC,
∴MD=MB,
∵∠BAC=30°,∠CAD=45°,
∴∠BMC=60°,∠DMC=90°,
∴∠BMD=30°,
∴∠BDM==75°,
∵∠MDA=45°
∴∠EDB=180°﹣∠BDM﹣∠MDA=60°,
令ED=x,则BE=x,AD=2,AB=2,
∴由Rt△ABE可得:(2)2=(x)2+(x+2)2,
解得x=,则BD=2,
∵M、N分别是AC,BD中点,
∴MD=2 DN=.
由Rt△MND可得:
MN==.
【点评】本题综合考查了等腰三角形的性质和解直角三角形的方法,同时考查了分类讨论思想.
一.选择题(共12小题)
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
2.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2 B.4cm C. D.
3.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
A.6.5米 B.9米 C.13米 D.15米
4.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )
A.(﹣1,) B.(0,) C.(,0) D.(1,)
5.AB是⊙O的弦,∠AOB=80°,则弦AB所对的圆周角是( )
A.40° B.140°或40° C.20° D.20°或160°
6.如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
A.115° B.110° C.90° D.80°
7.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
8.如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M B.点N C.点P D.点Q
9.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.均不可能
10.已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q.则下列说法中正确的个数为( )
①CO⊥AD;②∠COB=2∠GDC;③P是△ACQ的外心;④若tan∠ABC=,CF=8,则CQ=;⑤(FP+PQ)2=FP?FG;⑥PQ=QD.
A.3 B.4 C.5 D.6
11.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
12.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
二.填空题(共8小题)
13.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= .
14.如图所示,点A是半圆上的一个三等分点,B是劣弧的中点,点P是直径MN上的一个动点,⊙O的半径为1,则AP+PB的最小值 .
15.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
16.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则弧的度数是 .
17.在△ABC中,∠BAC=90°,AB=AC,D为△ABC形外一点,且AD=AC,则∠BDC的度数为 .
18.如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC= .
19.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 .
20.P为⊙O内一点,OP=3cm,⊙O的半径为5cm,则经过P点的最短弦长为 cm,最长弦长为 cm.
三.解答题(共8小题)
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
22.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
23.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?
24.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交于AB于C、D两点,求证:AC=BD.
25.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.
(1)求直径AB的长;
(2)求阴影部分的面积(结果保留π).
26.如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD?DC=PA?BC.
27.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
28.已知直角三角形ABC和ADC有公共斜边AC,M、N分别是AC,BD中点,且M、N不重合.
(1)线段MN与BD是否垂直?请说明理由;
(2)若∠BAC=30°,∠CAD=45°,AC=4,求MN的长.
2020年北师大版数学下册九年级《第3章 圆》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
【分析】根据等弧的定义对A进行判断;根据垂径定理对B进行判断;根据圆心角、弧、弦的关系对C进行判断;根据圆的对称性对D进行判断.
【解答】解:A、能完全重合的两条弧是等弧,所以A选项错误;
B、平分弦(非直径)的直径垂直于弦,所以B选项错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以C选项错误;
D、经过圆心的每一条直线都是圆的对称轴,所以D选项正确.
故选:D.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了垂径定理和圆心角、弧、弦的关系.
2.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2 B.4cm C. D.
【分析】连接AO,过O作OD⊥AB,交于点D,交弦AB于点E,根据折叠的性质可知OE=DE,再根据垂径定理可知AE=BE,在Rt△AOE中利用勾股定理即可求出AE的长,进而可求出AB的长.
【解答】解:如图所示,
连接AO,过O作OD⊥AB,交于点D,交弦AB于点E,
∵折叠后恰好经过圆心,
∴OE=DE,
∵⊙O的半径为4,
∴OE=OD=×4=2,
∵OD⊥AB,
∴AE=AB,
在Rt△AOE中,
AE===2.
∴AB=2AE=4.
故选:B.
【点评】本题考查的是垂径定理在实际生活中的运用及翻折变换的性质,根据题意画出图形,作出辅助线利用数形结合解答.
3.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
A.6.5米 B.9米 C.13米 D.15米
【分析】根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O.
连接OA.根据垂径定理和勾股定理求解.
【解答】解:根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O
连接OA.根据垂径定理,得AD=6
设圆的半径是r,根据勾股定理,得r2=36+(r﹣4)2,解得r=6.5
故选:A.
【点评】此题综合运用了勾股定理以及垂径定理.注意构造由半径、半弦、弦心距组成的直角三角形进行有关的计算.
4.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )
A.(﹣1,) B.(0,) C.(,0) D.(1,)
【分析】连接OQ、OP,求出∠POQ的度数,得出等边三角形POQ,得出PQ=OQ=OP=2,∠OPQ=∠OQP=60°,求出∠AOQ度数,根据三角形的内角和定理求出∠QAO,求出AQ、OA,即可得出答案.
【解答】解:连接OQ、PO,
则∠POQ=120°﹣60°=60,
∵PO=OQ,
∴△POQ是等边三角形,
∴PQ=OP=OQ=×4cm=2cm,∠OPQ=∠OQP=60°,
∵∠AOQ=90°﹣60°=30°,
∴∠QAO=180°﹣60°﹣30°=90°,
∴AQ=OQ=1cm,
∵在Rt△AOQ中,由勾股定理得:OA==,
∴A的坐标是(0,),
故选B.
方法二:由于是选择题,只有B选项在y轴上,
故选:B.
【点评】本题考查了圆心角、弧、弦之间的关系,三角形的内角和定理,勾股定理,等边三角形的性质和判定等知识点,解此题的关键是构造三角形后求出OA的长,主要考查学生分析问题和解决问题的能力.
5.AB是⊙O的弦,∠AOB=80°,则弦AB所对的圆周角是( )
A.40° B.140°或40° C.20° D.20°或160°
【分析】此题要分两种情况:当圆周角的顶点在优弧上时;当圆周角的顶点在劣弧上时;通过分析,从而得到答案.
【解答】解:当圆周角的顶点在优弧上时,根据圆周角定理,得圆周角:
∠ACB=∠AOB=×80°=40°;
当圆周角的顶点在劣弧上时,根据圆内接四边形的性质,得此圆周角:
∠ADB=180°﹣∠ACB=180°﹣40°=140°;
所以弦AB所对的圆周角是40°或140°.
故选:B.
【点评】注意:弦所对的圆周角有两种情况,且两种情况的角是互补的关系.
6.如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
A.115° B.110° C.90° D.80°
【分析】由四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,根据圆的内接四边形的性质,即可求得∠ADC的度数,继而求得答案.
【解答】解:∵四边形ABCD内接于圆O,∠B=110°,
∴∠ADC=180°﹣∠B=70°,
∴∠ADE=180°﹣∠ADC=110°.
故选:B.
【点评】此题考查了圆的内接多边形的性质.注意圆的内接四边形的对角互补.
7.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
【分析】设⊙O的半径为r,QO=m,则QP=m,QC=r+m,QA=r﹣m.利用相交弦定理,求出m与r的关系,即用r表示出m,即可表示出所求比值.
【解答】解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA?QC=QP?QD.
即(r﹣m)(r+m)=m?QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选:D.
【点评】本题考查了相交弦定理,即“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”.熟记并灵活应用定理是解题的关键.
8.如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A.点M B.点N C.点P D.点Q
【分析】连接OM,ON,OQ,OP,由线段垂直平分线的性质可得出OM=ON=OQ,据此可得出结论.
【解答】解:连接OM,ON,OQ,OP,
∵MN、MQ的垂直平分线交于点O,
∴OM=ON=OQ,
∴M、N、Q再以点O为圆心的圆上,OP与ON的大小不能确定,
∴点P不一定在圆上.
故选:C.
【点评】本题考查的是点与圆的位置关系及线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.
9.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.均不可能
【分析】要确定圆的大小需知道其半径.根据垂径定理知第①块可确定半径的大小.
【解答】解:第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
【点评】本题考查了垂径定理的应用,确定圆的条件,解题的关键是熟练掌握:圆上任意两弦的垂直平分线的交点即为该圆的圆心.
10.已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q.则下列说法中正确的个数为( )
①CO⊥AD;②∠COB=2∠GDC;③P是△ACQ的外心;④若tan∠ABC=,CF=8,则CQ=;⑤(FP+PQ)2=FP?FG;⑥PQ=QD.
A.3 B.4 C.5 D.6
【分析】①由于C是弧AD的中点,根据垂径定理即可证明CO⊥AD;
②根据圆内接四边形的性质可得∠GDC=∠BAC,根据圆周角等量可得∠COB=2∠BAC,等量代换可得∠COB=2∠GDC;
③由于AB是⊙O的直径,则∠ACB=90°,只需证明P是Rt△ACQ斜边AQ的中点即可;由垂径定理易知弧AC=弧AE,而C是弧AD的中点,那么弧CD=弧AE,即∠PAC=∠PCA,根据等角的余角相等,还可得到∠AQC=∠PCQ,由此可证得AP=PC=PQ,即P是△ACQ的外心;
④由③的相等弧可知:∠ABC=∠ACE=∠CAQ,那么它们的正切值也相等;在Rt△CAF中,根据CF的长及∠ACF的正切值,通过解直角三角形可求得AC的长,进而可在Rt△CAQ中,根据∠CAQ的正切值求出CQ的长;
⑤由③知:PQ=CP,则所求的乘积式可化为:CF2=FP?FG;在Rt△ACB中,由射影定理得:CF2=AF?FB,因此只需证明AF?FB=FG?FP即可,将上式化成比例式,证线段所在的三角形相似即可,即证Rt△AFP∽Rt△GFB;
⑥根据题目已知无法证明PQ=QD,依此即可作出判断.
【解答】①证明∵C是弧AD的中点,
∴∴弧AC=弧CD,
∴CO⊥AD;
②∵四边形ABDC是圆内接四边形,
∴∠GDC=∠BAC,
∵∠COB=2∠BAC,
∴∠COB=2∠GDC;
③证明:∵C是弧AD的中点,
∴弧AC=弧CD,
∴∠CAD=∠ABC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠CAD+∠AQC=90°
又∵CE⊥AB,
∴∠ABC+∠PCQ=90°
∴∠AQC=∠PCQ
∴在△PCQ中,PC=PQ,
∵CE⊥直径AB,
∴弧AC=弧AE,
∴弧AE=弧CD,
∴∠CAD=∠ACE.
∴在△APC中,有PA=PC,
∴PA=PC=PQ
∴P是△ACQ的外心.
④解:∵CE⊥直径AB于F,
∴在Rt△BCF中,由tan∠ABC==,CF=8,
得BF=.
∴由勾股定理,得BC==,
∵AB是⊙O的直径,
∴在Rt△ACB中,由tan∠ABC==,BC=,
∴AC=10,
易知Rt△ACB∽Rt△QCA,
∴AC2=CQ?BC,
∴CQ==;
⑤证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
又∵CF⊥AB,
∴∠ABG+∠G=90°,
∴∠DAB=∠G;
∴Rt△AFP∽Rt△GFB,
∴=,即AF?BF=FP?FG
易知Rt△ACF∽Rt△CBF,
∴CF2=AF?BF(或由射影定理得)
∴FC2=PF?FG,
由③,知PC=PQ,
∴FP+PQ=FP+PC=FC
∴(FP+PQ)2=FP?FG;
⑥由题目条件无法得到PQ=QD.
故选:C.
【点评】此题考查了三角形的外接圆与外心,圆周角定理,相似三角形的判定与性质,涉及的知识点有:圆心角、弧的关系,垂径定理,圆内接四边形的性质,圆周角定理,三角形的外接圆与外心,勾股定理以及相似三角形的判定和性质等知识,综合性较强,有一定的难度.
11.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
【分析】根据直线和圆的位置关系判断方法,可得结论.
【解答】解:∵d=3<半径=4
∴直线与圆相交
∴直线m与⊙O公共点的个数为2个
故选:C.
【点评】本题考查了直线与圆的位置关系,掌握直线和圆的位置关系判断方法:设⊙O的半径为r,圆心O到直线l的距离为d.①直线l和⊙O相交?d<r②直线l和⊙O相切?d=r,③直线l和⊙O相离?d>r.
12.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
【分析】首先连接OP、OQ,根据勾股定理知PQ2=OP2﹣OQ2,可得当OP⊥AB时,即线段PQ最短,然后由勾股定理即可求得答案.
【解答】解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2﹣OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3,
∴AB=OA=6,
∴OP==3,
∴PQ==2.
故选:C.
【点评】本题考查了切线的性质、等腰直角三角形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意得到当PO⊥AB时,线段PQ最短是关键.
二.填空题(共8小题)
13.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= 50° .
【分析】如图,连接BE.由圆周角定理和三角形内角和定理求得∠ABE=25°,再由“同弧所对的圆周角是所对的圆心角的一半”进行答题.
【解答】解:如图,连接BE.
∵BC为⊙O的直径,
∴∠CEB=∠AEB=90°,
∵∠A=65°,
∴∠ABE=25°,
∴∠DOE=2∠ABE=50°,(圆周角定理)
故答案为:50°.
【点评】本题考查了圆的认识及三角形的内角和定理等知识,难度不大.
14.如图所示,点A是半圆上的一个三等分点,B是劣弧的中点,点P是直径MN上的一个动点,⊙O的半径为1,则AP+PB的最小值 .
【分析】本题是要在MN上找一点P,使PA+PB的值最小,设A′是A关于MN的对称点,连接A′B,与MN的交点即为点P.此时PA+PB=A′B是最小值,可证△OA′B是等腰直角三角形,从而得出结果.
【解答】解:作点A关于MN的对称点A′,连接A′B,交MN于点P,连接OA′,OA,OB,PA,AA′.
∵点A与A′关于MN对称,点A是半圆上的一个三等分点,
∴∠A′ON=∠AON=60°,PA=PA′,
∵点B是弧AN的中点,
∴∠BON=30°,
∴∠A′OB=∠A′ON+∠BON=90°,
又∵OA=OA′=1,
∴A′B=.
∴PA+PB=PA′+PB=A′B=.
故答案为:.
【点评】本题结合图形的性质,考查轴对称﹣﹣最短路线问题.其中求出∠BOA′的度数是解题的关键.
15.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
【分析】连接OC,利用垂径定理解答即可.
【解答】解:连接OC,
∵直尺一边与量角器相切于点C,
∴OC⊥AD,
∵AD=10,∠DOB=60°,
∴∠DAO=30°,
∴OE=,OA=,
∴CE=OC﹣OE=OA﹣OE=,
故答案为:
【点评】此题考查垂径定理,关键是利用垂径定理解答.
16.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则弧的度数是 150° .
【分析】作辅助线,证明△AGO是等边三角形,则∠AOG=60°,同理∠BOG=60°,所以∠BOC=90°+60°=150°,根据圆心角的度数等于弧的度数可以得出结论.
【解答】解:如图,
过O作OG⊥AB,交⊙O于G,交AB于H,连接AG、AO,
由折叠得:GH=OH,
∴AG=AO,
∵AO=OG,
∴AO=OG=AG,
∴△AGO是等边三角形,
∴∠AOG=60°,
同理∠BOG=60°,
∴∠BOC=90°+60°=150°,
则弧的度数是150°;
故答案为:150°.
【点评】本题考查了圆心角、弧、弦的性质、垂径定理、等腰三角形的三线合一的性质、翻折变换,明确翻折前后的边相等,熟练掌握垂径定理、等腰三角形的三线合一的性质是关键.
17.在△ABC中,∠BAC=90°,AB=AC,D为△ABC形外一点,且AD=AC,则∠BDC的度数为 45°或135° .
【分析】首先根据题意画出图形,由AB=AC,AD=AC,可得点B,C,D在以A为圆心,AB为半径的圆上,然后由圆周角定理与圆的内接四边形的性质,求得∠BDC的度数.
【解答】解:如图,∵AB=AC,AD=AC,
∴点B,C,D在以A为圆心,AB为半径的圆上,
∴∠BDC=∠BAC=×90°=45°,
∠BD′C=180°﹣∠BDC=135°.
∴∠BDC的度数为45°或135°.
故答案为:45°或135°.
【点评】此题考查了圆周角定理以及圆的内接四边形的性质.注意根据题意画出图形,得到点B,C,D在以A为圆心,AB为半径的圆上是关键.
18.如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC= 60° .
【分析】设∠ADC的度数=α,∠ABC的度数=β,由题意可得,求出β即可解决问题.
【解答】解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠AOC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故答案为:60°.
【点评】该题主要考查了圆周角定理及其应用问题;应牢固掌握该定理并能灵活运用.
19.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 4 .
【分析】利用相交弦定理,可以求出CE的长,从而知道CD的长,就可求出⊙O的半径.
【解答】解:根据相交弦定理,AE?BE=CE?DE,
又∵BE=3,AE=4,DE=2,
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4.
故此题应该填4.
【点评】此题考查了相交弦定理,先求出直径,再得出半径.
20.P为⊙O内一点,OP=3cm,⊙O的半径为5cm,则经过P点的最短弦长为 8 cm,最长弦长为 10 cm.
【分析】当弦与OP垂直时,弦最短,过P点经过圆心的弦最长.
【解答】解:当弦与OP垂直时,弦最短,最短弦为8cm,
过P点经过圆心的弦最长为直径,最长弦为10cm.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
三.解答题(共8小题)
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
【分析】连结OC、OD,由OA=OB,AE=BF,得到OE=OF,由CE⊥AB,DF⊥AB得到∠OEC=∠OFD=90°,再根据“HL”可判断Rt△OEC≌Rt△OFD,则∠COE=∠DOF,所以AC弧=BD弧,AC=BD.
【解答】解:AC与BD相等.理由如下:
连结OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了直角三角形全等的判定与性质.
22.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
【分析】过O作OF垂直于CD,连接OD,利用垂径定理得到F为CD的中点,由AE+EB求出直径AB的长,进而确定出半径OA与OD的长,由OA﹣AE求出OE的长,在直角三角形OEF中,利用30°所对的直角边等于斜边的一半求出OF的长,在直角三角形ODF中,利用勾股定理求出DF的长,由CD=2DF即可求出CD的长.
【解答】解:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA﹣AE=4﹣2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,
则CD=2DF=2.
【点评】此题考查了垂径定理,勾股定理,以及含30°直角三角形的性质,利用了转化的思想,熟练掌握定理是解本题的关键.
23.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?
【分析】连接OA构成直角三角形,先根据垂径定理,由DE垂直AB得到点E为AB的中点,由AB=10可求出AE的长,再设出圆的半径OA为x,表示出OE,根据勾股定理建立关于x的方程,求出方程的解即可得到x的值,即为圆的半径,把求出的半径代入即可得到答案.
【解答】解:连接OA,∵AB⊥CD,且AB=10,
∴AE=BE=5,
设圆O的半径OA的长为x,则OC=OD=x
∵CE=1,
∴OE=x﹣1,
在直角三角形AOE中,根据勾股定理得:
x2﹣(x﹣1)2=52,化简得:x2﹣x2+2x﹣1=25,
即2x=26,
解得:x=13
所以CD=26(寸).
【点评】此题考查了学生对垂径定理的运用与掌握,注意利用圆的半径,弦的一半及弦心距所构成的直角三角形来解决实际问题,做此类题时要多观察,多分析,才能发现线段之间的联系.
24.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交于AB于C、D两点,求证:AC=BD.
【分析】连接OA、OB,根据半径相等得到∠A=∠B,根据等弧所对的圆周角相等得到∠AOC=∠BOD,根据三角形全等的判定定理证明△AOC≌△BOD,根据全等三角形的性质证明结论.
【解答】证明:连接OA、OB,
∵OA=OB,
∴∠A=∠B,
∵=,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD.
【点评】本题考查的是圆心角、弧、弦的关系以及三角形全等的判定和性质,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等是解题的关键.
25.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.
(1)求直径AB的长;
(2)求阴影部分的面积(结果保留π).
【分析】(1)根据直径所对的圆周角是直角推知∠ACB=90°,然后在直角三角形ABC中利用边角关系、勾股定理来求直径AB的长度;
(2)连接OD.利用(1)中求得AB=4可以推知OA=OD=2;然后由角平分线的性质求得∠AOD=90°;最后由扇形的面积公式、三角形的面积公式可以求得
阴影部分的面积=S扇形△AOD﹣S△AOD.
【解答】解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,…(1分)
∵∠B=30°,
∴AB=2AC,…(3分)
∵AB2=AC2+BC2,
∴AB2=AB2+62,…(5分)
∴AB=4. …(6分)
(2)连接OD.
∵AB=4,∴OA=OD=2,…(8分)
∵CD平分∠ACB,∠ACB=90°,
∴∠ACD=45°,
∴∠AOD=2∠ACD=90°,…(9分)
∴S△AOD=OA?OD=?2?2=6,…(10分)
∴S扇形△AOD=?π?OD2=?π?(2)2=3π,…(11分)
∴阴影部分的面积=S扇形△AOD﹣S△AOD=3π﹣6. …(12分)
【点评】本题综合考查了圆周角定理、含30度角的直角三角形以及扇形面积公式.解答(2)题时,采用了“数形结合”的数学思想.
26.如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD?DC=PA?BC.
【分析】要证AD?DC=PA?BC,需证△PAD∽△DCB;由DP∥AC,可得∠ADP=∠DAC=∠DBC;由于∠DAP是圆内接四边形ABCD的一个外角,故有∠DAP=∠DCB;从而△PAD∽△DCB成立,由此得证.
【解答】证明:如图,连接AC,连接BD.
∵DP∥AC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB.
∴△PAD∽△DCB.
得PA:DC=AD:BC,
即AD?DC=PA?BC.
【点评】本题考查了平行线的性质,圆周角定理,相似三角形的判定和性质等知识.
27.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 (2,0) ;
(3)判断点D(5,﹣2)与⊙M的位置关系.
【分析】(1)由网格容易得出AB的垂直平分线和BC的垂直平分线,它们的交点即为点M;
(2)根据图形即可得出点M的坐标
(3)用两点间距离公式求出圆的半径和线段DM的长,当DM小于圆的半径时点D在圆内.
【解答】解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).
故答案为(2,0);
(3)圆的半径AM==2.
线段MD==<2,
所以点D在⊙M内.
【点评】本题考查的是点与圆的位置关系,坐标与图形性质以及垂径定理,利用网格结构得到圆心M的坐标是解题的关键.
28.已知直角三角形ABC和ADC有公共斜边AC,M、N分别是AC,BD中点,且M、N不重合.
(1)线段MN与BD是否垂直?请说明理由;
(2)若∠BAC=30°,∠CAD=45°,AC=4,求MN的长.
【分析】(1)根据题意画出图形,再作出辅助线构成等腰三角形,利用等腰三角形的性质进行证明;
(2)注意要分二种情况讨论:即B、D在AC两侧和B、D在AC同侧.
【解答】解:(1)线段MN与BD垂直.
连接MB与MD,由直角三角形斜边上的中线等于斜边长的一半,可以知道
MB=,MD=,所以MB=MD.
三角形MBD中,N是底边上的中点,等腰三角形的性质可以说明:
MN垂直BD.
(2)如图一:连接BM、MD,延长DM,过B作DM延长线的垂线段BE,
∵M是AC的中点,
∴MD⊥AC,△BCM是等边三角形,
∴在Rt△BEM中,∠EMB=30°,
∵AC=4,∴BM=2,
∴BE=1,EM=,MD=2,
从而可知
BD==2
∴BN=.
由Rt△BMN可得:
MN==.
如图二:连接BM、MD,延长AD,过B作垂线段BE,
∵M、N分别是AC,BD中点,
∴MD=AC,MBAC,
∴MD=MB,
∵∠BAC=30°,∠CAD=45°,
∴∠BMC=60°,∠DMC=90°,
∴∠BMD=30°,
∴∠BDM==75°,
∵∠MDA=45°
∴∠EDB=180°﹣∠BDM﹣∠MDA=60°,
令ED=x,则BE=x,AD=2,AB=2,
∴由Rt△ABE可得:(2)2=(x)2+(x+2)2,
解得x=,则BD=2,
∵M、N分别是AC,BD中点,
∴MD=2 DN=.
由Rt△MND可得:
MN==.
【点评】本题综合考查了等腰三角形的性质和解直角三角形的方法,同时考查了分类讨论思想.
