人教版七年级数学下册 第6章 实数 章末复习课件(共37张PPT)
文档属性
| 名称 | 人教版七年级数学下册 第6章 实数 章末复习课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 881.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览








文档简介
(共37张PPT)
第6章 实数
章末复习
学习目标:
(1)回顾算术平方根、平方根、立方根的概念.
(2)会求一个数的算术平方根、平方根或立方根.
(3)回顾无理数和实数的概念,知道实数和数轴上的点的一一对应关系.
(4)会进行实数的有关计算.
学习重、难点:
重点:算术平方根、平方根、立方根、无理数和实数的概念.
难点:概念的理解和运用.
复习导入
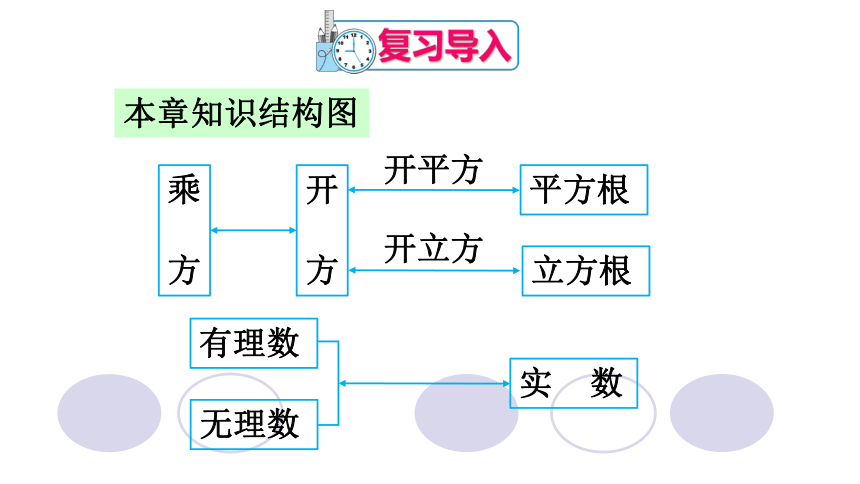
本章知识结构图
乘
方
开
方
平方根
立方根
开平方
开立方
有理数
无理数
实 数
自主复习
1
平方根的概念是什么?算术平方根的概念是什么?这两个概念的区别与联系是什么?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.
如果这个数是正数,那么这个数是a的算术平方根.
x2 = a,
x= (算术平方根)或
立方根的概念是什么?
2
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根或三次方根.
如果x3 = a,那么x叫做a的立方根.
x=
3
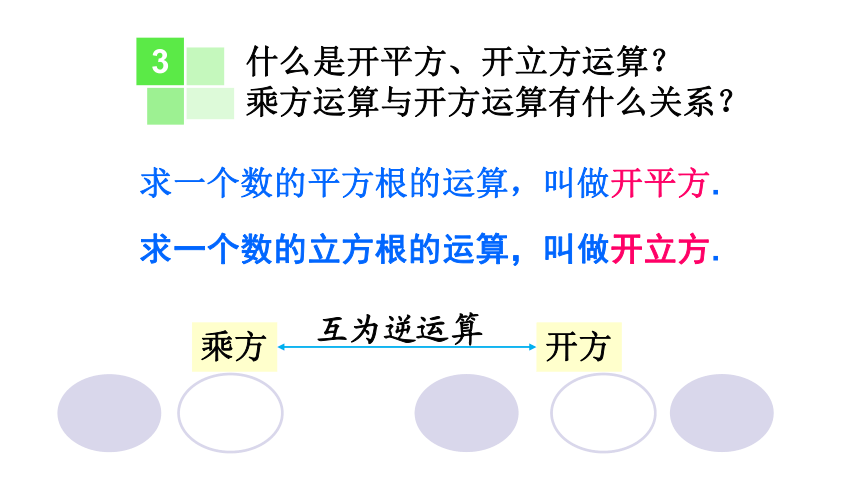
什么是开平方、开立方运算?
乘方运算与开方运算有什么关系?
求一个数的平方根的运算,叫做开平方.
求一个数的立方根的运算,叫做开立方.
乘方
开方
互为逆运算
4
无理数和有理数的区别是什么?
无理数不能表示成两个整数之比,是无限不循环小数.
有理数是能够表示成两个整数之比的数,是整数或有限小数.
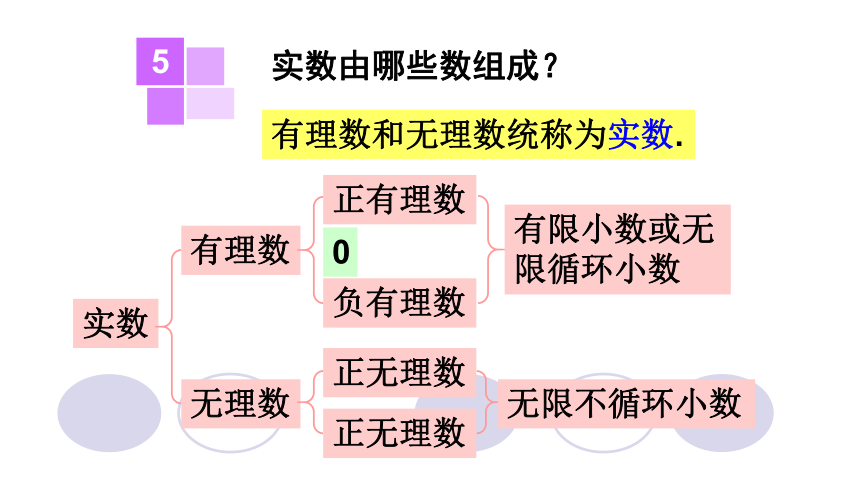
实数由哪些数组成?
5
有理数和无理数统称为实数.
实数
有理数
无理数
正有理数
0
负有理数
正无理数
正无理数
有限小数或无限循环小数
无限不循环小数
实数与数轴上的点有什么关系?
6
实数与数轴上的点是“一一对应”的.
7
数的范围是怎样从正整数逐步扩充到实数的?随着数的不断扩充,数的运算有什么发展?加法与乘法的运算律始终保持不变吗?
运算:加、减、乘、除、乘方、开方.
运算律:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律.
实
数
运
算
典例精析
例1 已知一个正数的平方根分别是x+3和x – 1,求这个正数的立方根.
解:由正数有两个平方根,他们互为相反数得:
x + 3 + x – 1 =0,解得x = – 1,
所以这个正数是(x + 3)2 = 4
所以这个正数的立方根是
例2 计算
(1)
解:原式=
= – 1
(2) (精确到0.1)
解:原式=
≈ 3.14 – 1.41
≈ 1.7
例3 比较大小: 与 .
解:∵
∴
例4 若a,b两个实数在数轴上的位置,如图所示,设M=a+b,N= – a +b,H= a – b,
G= – a – b ,则下列各式中正确的是( )
0
-1
1
b
a
A.M>N>H>G B.H>M>G>N
C.H>M>N>G D.G>H>M>N
B
解析:由图可知 a >1, – 1 < b < 0,
∴ a – b > a + b > 0,– a + b < – a – b <0,
∴ a – b > a + b > – a – b > – a + b,
即 H > M > G > N.
基础巩固
随堂演练
1.(– 0 .7)2的平方根是( )
A.– 0 .7 B.±0.7 C.0.7 D.0.49
2.下列各组数中,互为相反数的一组是( )
A.– 2 与 B.– 2 与
C.– 2 与 D.│– 2 │与– (– 2 )
B
A
3.下列说法中正确的说法的个数为( )
(1)无理数就是开方开不尽的数;(2)无理数就是无限小数;(3)无理数包括正无理数,零,负无理数;(4)无理数都可以用数轴上的点来表示.
A.1 B.2 C.3 D.4
4.若a2 = 36,|b| = 3,则a – b =( )
A. – 9 B.±9 C.±3 D.±9或±3
A
D
综合运用
9.若│x2 –25│+ = 0,则 x =____,y =____.
10.求式子27(x+1)3 + 64 = 0中x的值.
解:∵27(x+1)3 +64=0,
∴(x+1)3 = ,
∴ x + 1 = ,∴x = .
±5
3
伸
延
展
拓
11.填空:
(1)一个数的平方等于它本身,这个数是________;一个数的平方根等于它本身,这个数是___,一个数的算术平方根等于它本身,这个数是________.
(2)一个数的立方等于它本身,这个数是___________;一个数的立方根等于它本身,这个数是____________.
0或1
0或1
0
0或1或– 1
0或1或– 1
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
本课时教学可应用不同形式的练习引导学生认识相关的基本概念,强化对基本概念的理解以利于进行运算与判断.注重分类思想的认识与理解,强调实数计算能力的训练,打下坚实的运算能力的基础.
复习题6
复习巩固
综合运用
拓广探索
第6章 实数
章末复习
学习目标:
(1)回顾算术平方根、平方根、立方根的概念.
(2)会求一个数的算术平方根、平方根或立方根.
(3)回顾无理数和实数的概念,知道实数和数轴上的点的一一对应关系.
(4)会进行实数的有关计算.
学习重、难点:
重点:算术平方根、平方根、立方根、无理数和实数的概念.
难点:概念的理解和运用.
复习导入
本章知识结构图
乘
方
开
方
平方根
立方根
开平方
开立方
有理数
无理数
实 数
自主复习
1
平方根的概念是什么?算术平方根的概念是什么?这两个概念的区别与联系是什么?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.
如果这个数是正数,那么这个数是a的算术平方根.
x2 = a,
x= (算术平方根)或
立方根的概念是什么?
2
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根或三次方根.
如果x3 = a,那么x叫做a的立方根.
x=
3
什么是开平方、开立方运算?
乘方运算与开方运算有什么关系?
求一个数的平方根的运算,叫做开平方.
求一个数的立方根的运算,叫做开立方.
乘方
开方
互为逆运算
4
无理数和有理数的区别是什么?
无理数不能表示成两个整数之比,是无限不循环小数.
有理数是能够表示成两个整数之比的数,是整数或有限小数.
实数由哪些数组成?
5
有理数和无理数统称为实数.
实数
有理数
无理数
正有理数
0
负有理数
正无理数
正无理数
有限小数或无限循环小数
无限不循环小数
实数与数轴上的点有什么关系?
6
实数与数轴上的点是“一一对应”的.
7
数的范围是怎样从正整数逐步扩充到实数的?随着数的不断扩充,数的运算有什么发展?加法与乘法的运算律始终保持不变吗?
运算:加、减、乘、除、乘方、开方.
运算律:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律.
实
数
运
算
典例精析
例1 已知一个正数的平方根分别是x+3和x – 1,求这个正数的立方根.
解:由正数有两个平方根,他们互为相反数得:
x + 3 + x – 1 =0,解得x = – 1,
所以这个正数是(x + 3)2 = 4
所以这个正数的立方根是
例2 计算
(1)
解:原式=
= – 1
(2) (精确到0.1)
解:原式=
≈ 3.14 – 1.41
≈ 1.7
例3 比较大小: 与 .
解:∵
∴
例4 若a,b两个实数在数轴上的位置,如图所示,设M=a+b,N= – a +b,H= a – b,
G= – a – b ,则下列各式中正确的是( )
0
-1
1
b
a
A.M>N>H>G B.H>M>G>N
C.H>M>N>G D.G>H>M>N
B
解析:由图可知 a >1, – 1 < b < 0,
∴ a – b > a + b > 0,– a + b < – a – b <0,
∴ a – b > a + b > – a – b > – a + b,
即 H > M > G > N.
基础巩固
随堂演练
1.(– 0 .7)2的平方根是( )
A.– 0 .7 B.±0.7 C.0.7 D.0.49
2.下列各组数中,互为相反数的一组是( )
A.– 2 与 B.– 2 与
C.– 2 与 D.│– 2 │与– (– 2 )
B
A
3.下列说法中正确的说法的个数为( )
(1)无理数就是开方开不尽的数;(2)无理数就是无限小数;(3)无理数包括正无理数,零,负无理数;(4)无理数都可以用数轴上的点来表示.
A.1 B.2 C.3 D.4
4.若a2 = 36,|b| = 3,则a – b =( )
A. – 9 B.±9 C.±3 D.±9或±3
A
D
综合运用
9.若│x2 –25│+ = 0,则 x =____,y =____.
10.求式子27(x+1)3 + 64 = 0中x的值.
解:∵27(x+1)3 +64=0,
∴(x+1)3 = ,
∴ x + 1 = ,∴x = .
±5
3
伸
延
展
拓
11.填空:
(1)一个数的平方等于它本身,这个数是________;一个数的平方根等于它本身,这个数是___,一个数的算术平方根等于它本身,这个数是________.
(2)一个数的立方等于它本身,这个数是___________;一个数的立方根等于它本身,这个数是____________.
0或1
0或1
0
0或1或– 1
0或1或– 1
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
本课时教学可应用不同形式的练习引导学生认识相关的基本概念,强化对基本概念的理解以利于进行运算与判断.注重分类思想的认识与理解,强调实数计算能力的训练,打下坚实的运算能力的基础.
复习题6
复习巩固
综合运用
拓广探索
