人教版八年级数学 下册 18.1.1 平行四边形的性质 课件(2课时,共40张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 18.1.1 平行四边形的性质 课件(2课时,共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 15:18:24 | ||
图片预览







文档简介
(共39张PPT)
不管追求什么目标, 都应坚持不懈。
—— 爱因斯坦
18.1 平行四边形的性质
人教版八年级数学 下册
目标导航
1.归纳平行四边形的概念和表示方法。
2.探索并掌握平行四边形对边相等、对角相等、对角线互相平分的性质的性质。
3.利用平行四边形的性质解决一些实际问题。
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
复习回顾
我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗?
A
B
C
D
复习回顾
对于平行四边形,从定义出发,你能得出它的性质
吗?
你能证明这些结论吗?
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是
什么?
猜想:平行四边形对角相等,对边相等.
复习回顾
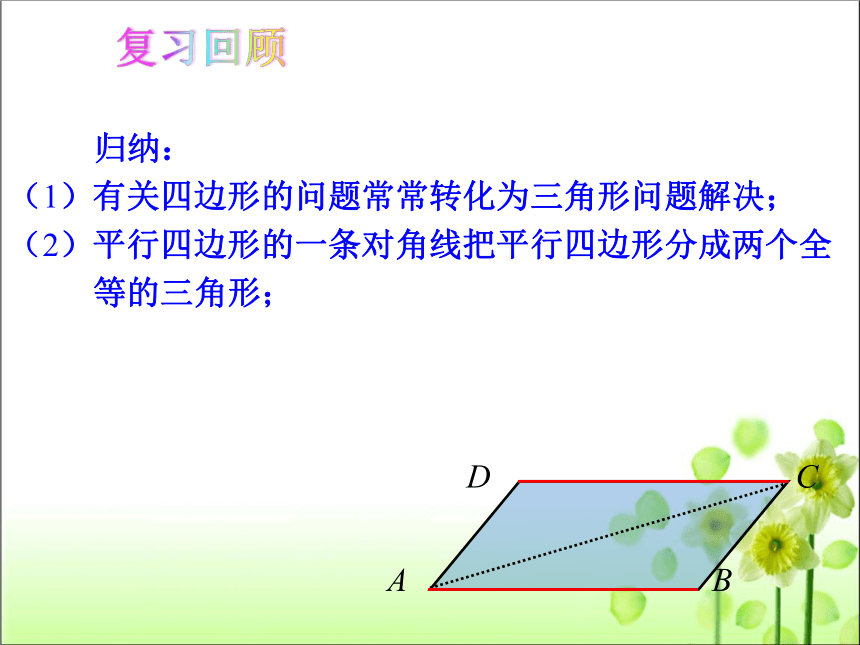
归纳:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全
等的三角形;
A
B
C
D
复习回顾
认真阅读课本第41至43页的内容,完成下面练习并体验知识点的形成过程.
自主研学
知识点一 平行四边形的概念
1、___________________________
叫做平行四边形.
2、平行四边形用“_____”
表示,如图,平行四边形
记作________________ .
两组对边分别平行的四边形
" ABCD "
合作探究
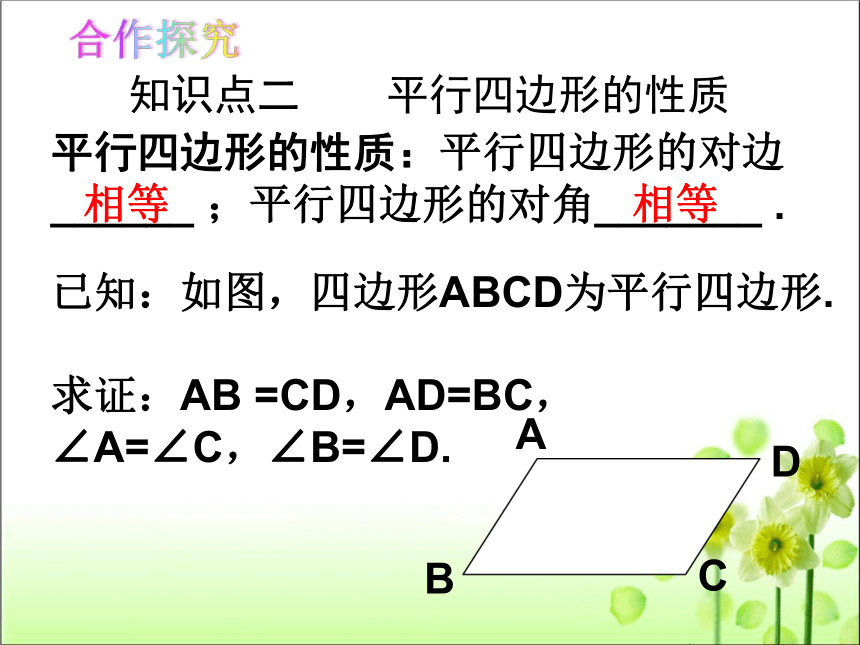
知识点二 平行四边形的性质
平行四边形的性质:平行四边形的对边______ ;平行四边形的对角_______ .
已知:如图,四边形ABCD为平行四边形.
求证:AB =CD,AD=BC,
∠A=∠C,∠B=∠D.
相等
相等
A
B
D
C
合作探究
1
2
4
3
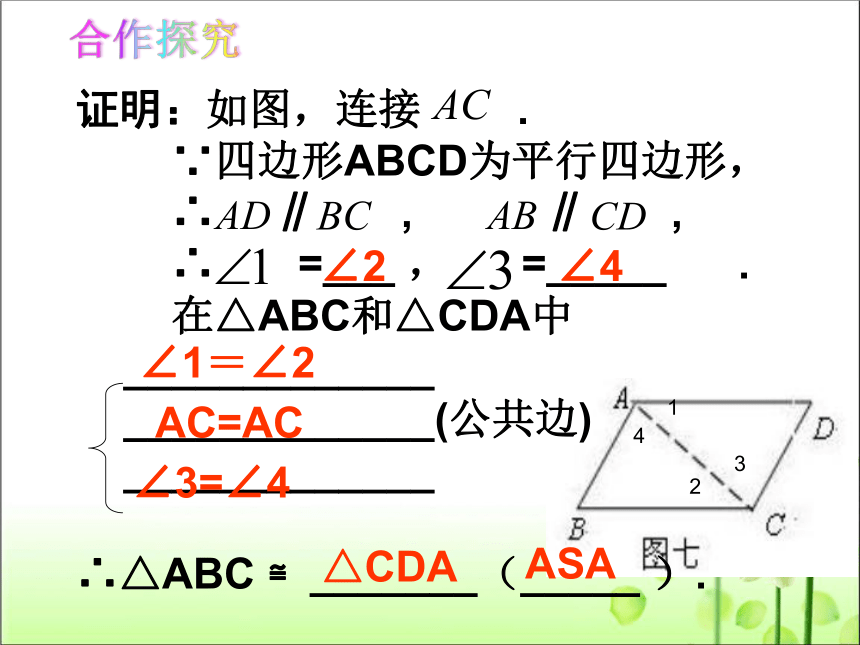
证明:如图,连接 .
∵四边形ABCD为平行四边形,
∴ ∥ , ∥ ,
∴ =___ , =_____ .
在△ABC和△CDA中
_____________
_____________(公共边)
_____________
∴△ABC ≌_______(_____ ).
∠2
∠4
∠1=∠2
AC=AC
∠3=∠4
△CDA
ASA
合作探究
1
2
4
3
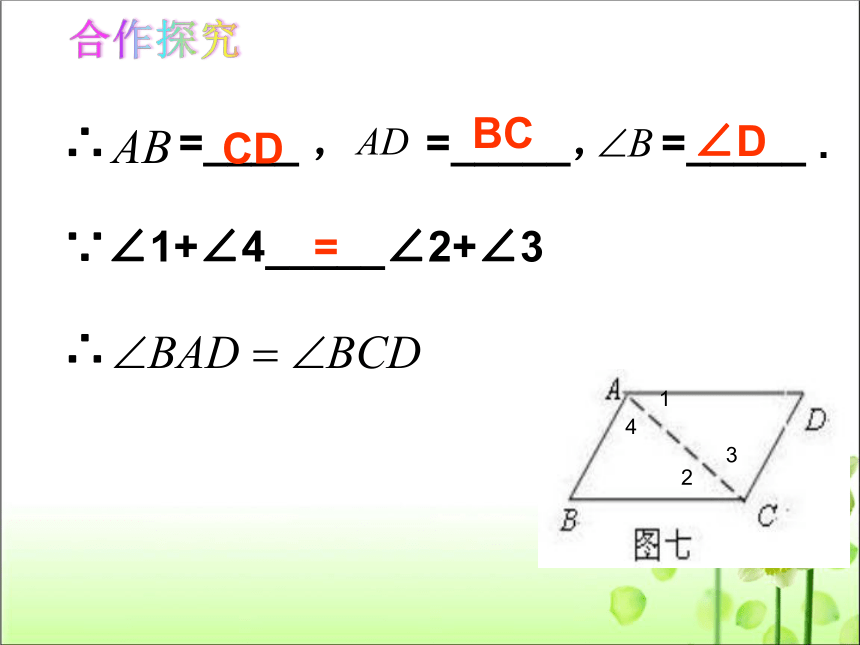
∴ =____ , =_____, =_____ .
∵∠1+∠4_____∠2+∠3
∴
CD
BC
∠D
=
合作探究
已知:如图,四边形ABCD为平行四边形.
求证:∠A=∠C,
∠B=∠D.
A
B
D
C
不添加辅助线直接运用平行四边形的定义证明其对角相等.
合作探究
证明:
∵四边形ABCD为平行四边形,
∴
AB∥CD,
AD∥BC .
∴∠A+∠D=180°,∠B+∠C=180°;
∠A+∠B=180°,∠C+∠D=180°.
(两直线平行,同旁内角互补.)
∴
A
B
D
C
∠A=∠C,∠B=∠D.
合作探究
1. ABCD中,若∠B=60°,则∠A=_____,∠C=_____,∠D=_____.
2、在 ABCD中,
(1)已知AB=5,BC=3,求它的周长;
120°
120°
60°
解: ABCD的周长=2(AB+BC)
=2(5+3)
=16.
即学即练
2、在 ABCD中,
(2)已知∠A=38°,求其余各内角的度数.
解:∵四边形ABCD为平行四边形,
∴∠C=∠A=38°
(平行四边形的对角相等),
∵AD∥BC(平行四边形的概念),
∴∠A+∠B=180°,
∴∠B=180°-∠A=180°-38°=142°,
∴∠D=∠B=142°
(平行四边形的对角相等)
即学即练
3、如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形.转动
其中一张纸条,
线段AD和BC
的长度有什么
关系?为什么?
即学即练
解:AD=BC,这时构成四边形ABCD的两
组对边分别平行,它是平行四边形,
根据平行四边形
对边相等的
性质,可知
AD=BC
你答对了吗
即学即练
结论 已知平行四边形一个内角的度数,那么其它内角的度数也_______确定
(填“能”或“不能”).
能
即学即练
知识点三 两条平行线之间的距离
例1 如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分
别为E、F.求证:AE=CF.
证明:∵四边形是平行四边形,
∴∠A=∠C,AD=BC,
又∠AED=∠CFB=90°,
∴△ADE≌△CBF,
∴AE=CF.
合作探究
结论 两条平行线之间的任何两条_________都相等. 两条平行线中,______________________________________,叫做这两条平行线之间的距离.
平行线段
一条直线上任意一点到另一条直线的距离
合作探究
思考 两条平行线之间的距离和点与点之间的距离、点到直线的距离有何联系与区别?
解:点与点之间有距离是定义点
到直线的距离、两条平行线
之间距离的基础,它们本
质上都是点与点之间的距离.
合作探究
2、平行四边形的性质:
___________________________________________________________.
1、_______________________________
叫做平行四边形.
两组对边分别平行的四边形
平行四边形的对边相等 ;
平行四边形的对角相等
3、两条平行线之间的任何两条___________都相等. 两条平行线中,____________________________________
________________,叫做这两条平行线之间的距离.
平行线段
一条直线上任意一点到另一条
直线的距离
归纳小结
1、平行四边形的对边 且 ; 平行四边形的对角 ,邻角 。
2、在 ABCD中,∠A= 500,则∠B= ,
∠C= ,∠D= .
3、平行四边形的周长为50cm,两邻边之比为 2:3,则两邻边分别为 。
平行
相等
相等
互补
1300
500
1300
10cm、15cm
A
B
C
D
小试牛刀
答(1)AB=CD、AD=BC;
4、画一个口ABCD,在这个图形中有哪那些线段相等?这体现了平行四边形的哪些性质? 再画出口ABCD的对角线AC和BD,它们交于点O.你还能得到图形有哪些线段相等?
A
B
C
D
(2)体现了平行四边形对边相等。
o
(3)AO=OC、BO=OD
小试牛刀
如图,在 ABCD中,连接AC,BD,并设它们相交
于点O.OA与OC,OB与OD有什么关系?
D
A
B
C
O
猜想:平行四边形的
对角线互相平分.
你能证明上述猜想吗?
提出猜想
如图,在 ABCD中,对角线AC,BD 相交于点O.
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
证明:∵ 四边形
ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
提出猜想
认真阅读课本第43至44页的内容,完成下面练习并体验知识点的形成过程.
自主研学
知识点一 平行四边形的性质
平行四边形的性质:平行四边形的对角线__________________.
互相平分
合作探究
已知:如图,在口ABCD中,对角线AC,BD交于点O.求证:OA= ___,OB= _ .
证明:∵四边形ABCD是平行四边形,
∴AB∥_____,AB=_____(平行四边形的性质)
∴∠1=∠2,∠3=∠4( )
在△AOB和△COD中
____________
____________
____________
∴_________________( )
∴OA= ,OB= .(全等三角形的对应边相等)
{
CD
CD
两直线平行,内错角相等
∠2=∠1
AB=CD
∠4=∠3
△AOB≌△COD
ASA
OC
OD
OC
OD
合作探究
1、判断对错
(1)在口ABCD中,AC交BD于O,则 AO=OB=OC=OD.( )
(2)平行四边形的两组对边分别平行且相等.( )
(3)平行四边形是轴对称图形.( )
×
√
×
即学即练
2、平行四边形一条对角线分一个内角为25°和35°,则4个内角分别为 .
3、平行四边形的两条对角线把它分成的四个三角形( )
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
60°、 120°、 60°、120°
即学即练
知识点二 平行四边形性质的应用
例2 如图,在口ABCD中,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及口ABCD的面积.
解:∵ 四边形ABCD是 ,
∴BC=AD= , CD= = .
∵ AC⊥BC,∴ΔABC是 三角形.
∴AC= = =6.
又 OA=OC ∴ OA= _____=3,
∴S口ABCD= · =8×6=48.
A
B
C
D
o
平行四边形
8
AB
10
直角
AC
BC
AC
合作探究
解:(1) ∵四边形ABCD是平行四边形
∴AD= BC=10、OA=4、OD=7
△AOD的周长=OA+OD+AD=4+7+10=21;
1、如图,在口ABCD中,BC=10,
AC=8,BD=14.△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
(2)△DBC比△ABC的周长长,长6
∵BD-AC=14-8 =6
即学即练
证明:
∵四边形ABCD是平行四边形
∴OA=OC,AB∥CD,
∴∠EAO=∠FCO,
在△AOE和△COF中,
2、如图,口ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.求证:OE=OF.
∠EAO=∠FCO
OA=OC
∠EOA=∠FOC
∴△AOE≌COF(ASA)
∴OE=OF
A
D
B
C
E
F
O
即学即练
定理:平行四边形的对角线互相平分.
我们证明了平行四边形具有以下性质:
(1)平行四边形的对边相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
课堂小结
解题思想:
研究平行四边形,常常把它转化为三角形问题.
A
B
C
D
O
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
不管追求什么目标, 都应坚持不懈。
—— 爱因斯坦
18.1 平行四边形的性质
人教版八年级数学 下册
目标导航
1.归纳平行四边形的概念和表示方法。
2.探索并掌握平行四边形对边相等、对角相等、对角线互相平分的性质的性质。
3.利用平行四边形的性质解决一些实际问题。
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
复习回顾
我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗?
A
B
C
D
复习回顾
对于平行四边形,从定义出发,你能得出它的性质
吗?
你能证明这些结论吗?
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是
什么?
猜想:平行四边形对角相等,对边相等.
复习回顾
归纳:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全
等的三角形;
A
B
C
D
复习回顾
认真阅读课本第41至43页的内容,完成下面练习并体验知识点的形成过程.
自主研学
知识点一 平行四边形的概念
1、___________________________
叫做平行四边形.
2、平行四边形用“_____”
表示,如图,平行四边形
记作________________ .
两组对边分别平行的四边形
" ABCD "
合作探究
知识点二 平行四边形的性质
平行四边形的性质:平行四边形的对边______ ;平行四边形的对角_______ .
已知:如图,四边形ABCD为平行四边形.
求证:AB =CD,AD=BC,
∠A=∠C,∠B=∠D.
相等
相等
A
B
D
C
合作探究
1
2
4
3
证明:如图,连接 .
∵四边形ABCD为平行四边形,
∴ ∥ , ∥ ,
∴ =___ , =_____ .
在△ABC和△CDA中
_____________
_____________(公共边)
_____________
∴△ABC ≌_______(_____ ).
∠2
∠4
∠1=∠2
AC=AC
∠3=∠4
△CDA
ASA
合作探究
1
2
4
3
∴ =____ , =_____, =_____ .
∵∠1+∠4_____∠2+∠3
∴
CD
BC
∠D
=
合作探究
已知:如图,四边形ABCD为平行四边形.
求证:∠A=∠C,
∠B=∠D.
A
B
D
C
不添加辅助线直接运用平行四边形的定义证明其对角相等.
合作探究
证明:
∵四边形ABCD为平行四边形,
∴
AB∥CD,
AD∥BC .
∴∠A+∠D=180°,∠B+∠C=180°;
∠A+∠B=180°,∠C+∠D=180°.
(两直线平行,同旁内角互补.)
∴
A
B
D
C
∠A=∠C,∠B=∠D.
合作探究
1. ABCD中,若∠B=60°,则∠A=_____,∠C=_____,∠D=_____.
2、在 ABCD中,
(1)已知AB=5,BC=3,求它的周长;
120°
120°
60°
解: ABCD的周长=2(AB+BC)
=2(5+3)
=16.
即学即练
2、在 ABCD中,
(2)已知∠A=38°,求其余各内角的度数.
解:∵四边形ABCD为平行四边形,
∴∠C=∠A=38°
(平行四边形的对角相等),
∵AD∥BC(平行四边形的概念),
∴∠A+∠B=180°,
∴∠B=180°-∠A=180°-38°=142°,
∴∠D=∠B=142°
(平行四边形的对角相等)
即学即练
3、如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形.转动
其中一张纸条,
线段AD和BC
的长度有什么
关系?为什么?
即学即练
解:AD=BC,这时构成四边形ABCD的两
组对边分别平行,它是平行四边形,
根据平行四边形
对边相等的
性质,可知
AD=BC
你答对了吗
即学即练
结论 已知平行四边形一个内角的度数,那么其它内角的度数也_______确定
(填“能”或“不能”).
能
即学即练
知识点三 两条平行线之间的距离
例1 如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分
别为E、F.求证:AE=CF.
证明:∵四边形是平行四边形,
∴∠A=∠C,AD=BC,
又∠AED=∠CFB=90°,
∴△ADE≌△CBF,
∴AE=CF.
合作探究
结论 两条平行线之间的任何两条_________都相等. 两条平行线中,______________________________________,叫做这两条平行线之间的距离.
平行线段
一条直线上任意一点到另一条直线的距离
合作探究
思考 两条平行线之间的距离和点与点之间的距离、点到直线的距离有何联系与区别?
解:点与点之间有距离是定义点
到直线的距离、两条平行线
之间距离的基础,它们本
质上都是点与点之间的距离.
合作探究
2、平行四边形的性质:
___________________________________________________________.
1、_______________________________
叫做平行四边形.
两组对边分别平行的四边形
平行四边形的对边相等 ;
平行四边形的对角相等
3、两条平行线之间的任何两条___________都相等. 两条平行线中,____________________________________
________________,叫做这两条平行线之间的距离.
平行线段
一条直线上任意一点到另一条
直线的距离
归纳小结
1、平行四边形的对边 且 ; 平行四边形的对角 ,邻角 。
2、在 ABCD中,∠A= 500,则∠B= ,
∠C= ,∠D= .
3、平行四边形的周长为50cm,两邻边之比为 2:3,则两邻边分别为 。
平行
相等
相等
互补
1300
500
1300
10cm、15cm
A
B
C
D
小试牛刀
答(1)AB=CD、AD=BC;
4、画一个口ABCD,在这个图形中有哪那些线段相等?这体现了平行四边形的哪些性质? 再画出口ABCD的对角线AC和BD,它们交于点O.你还能得到图形有哪些线段相等?
A
B
C
D
(2)体现了平行四边形对边相等。
o
(3)AO=OC、BO=OD
小试牛刀
如图,在 ABCD中,连接AC,BD,并设它们相交
于点O.OA与OC,OB与OD有什么关系?
D
A
B
C
O
猜想:平行四边形的
对角线互相平分.
你能证明上述猜想吗?
提出猜想
如图,在 ABCD中,对角线AC,BD 相交于点O.
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
证明:∵ 四边形
ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
提出猜想
认真阅读课本第43至44页的内容,完成下面练习并体验知识点的形成过程.
自主研学
知识点一 平行四边形的性质
平行四边形的性质:平行四边形的对角线__________________.
互相平分
合作探究
已知:如图,在口ABCD中,对角线AC,BD交于点O.求证:OA= ___,OB= _ .
证明:∵四边形ABCD是平行四边形,
∴AB∥_____,AB=_____(平行四边形的性质)
∴∠1=∠2,∠3=∠4( )
在△AOB和△COD中
____________
____________
____________
∴_________________( )
∴OA= ,OB= .(全等三角形的对应边相等)
{
CD
CD
两直线平行,内错角相等
∠2=∠1
AB=CD
∠4=∠3
△AOB≌△COD
ASA
OC
OD
OC
OD
合作探究
1、判断对错
(1)在口ABCD中,AC交BD于O,则 AO=OB=OC=OD.( )
(2)平行四边形的两组对边分别平行且相等.( )
(3)平行四边形是轴对称图形.( )
×
√
×
即学即练
2、平行四边形一条对角线分一个内角为25°和35°,则4个内角分别为 .
3、平行四边形的两条对角线把它分成的四个三角形( )
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
60°、 120°、 60°、120°
即学即练
知识点二 平行四边形性质的应用
例2 如图,在口ABCD中,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及口ABCD的面积.
解:∵ 四边形ABCD是 ,
∴BC=AD= , CD= = .
∵ AC⊥BC,∴ΔABC是 三角形.
∴AC= = =6.
又 OA=OC ∴ OA= _____=3,
∴S口ABCD= · =8×6=48.
A
B
C
D
o
平行四边形
8
AB
10
直角
AC
BC
AC
合作探究
解:(1) ∵四边形ABCD是平行四边形
∴AD= BC=10、OA=4、OD=7
△AOD的周长=OA+OD+AD=4+7+10=21;
1、如图,在口ABCD中,BC=10,
AC=8,BD=14.△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
(2)△DBC比△ABC的周长长,长6
∵BD-AC=14-8 =6
即学即练
证明:
∵四边形ABCD是平行四边形
∴OA=OC,AB∥CD,
∴∠EAO=∠FCO,
在△AOE和△COF中,
2、如图,口ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.求证:OE=OF.
∠EAO=∠FCO
OA=OC
∠EOA=∠FOC
∴△AOE≌COF(ASA)
∴OE=OF
A
D
B
C
E
F
O
即学即练
定理:平行四边形的对角线互相平分.
我们证明了平行四边形具有以下性质:
(1)平行四边形的对边相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
课堂小结
解题思想:
研究平行四边形,常常把它转化为三角形问题.
A
B
C
D
O
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
