人教版八年级数学 下册 18.1.2 平行四边形的判定 课件(3课时,共53张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 18.1.2 平行四边形的判定 课件(3课时,共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 813.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 00:00:00 | ||
图片预览









文档简介
(共53张PPT)
无所求则无所获。
——华罗庚
18.1.2 平等四边形的判定
人教版八年级数学 下册
目标导航
1.探究平行四边形的判定方法及三角形中位线的概念、定理。
2. 能利用平行四边形的判定方
法及三角形中位线概念和定理解决一些实际问题。
目标导航一
平形四边形的判定
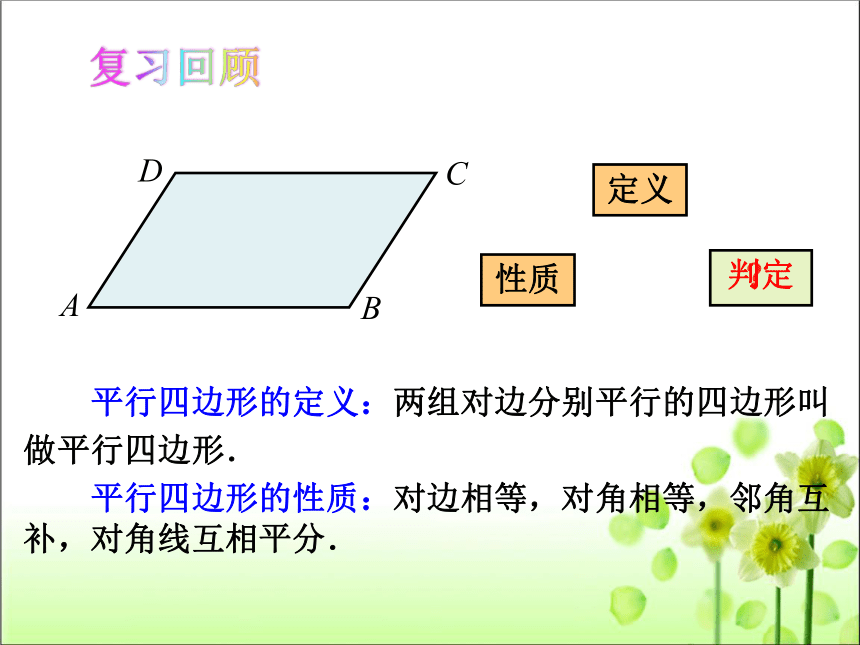
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,邻角互补,对角线互相平分.
?
判定
性质
定义
D
A
B
C
复习回顾
判定
性质
定义
D
A
B
C
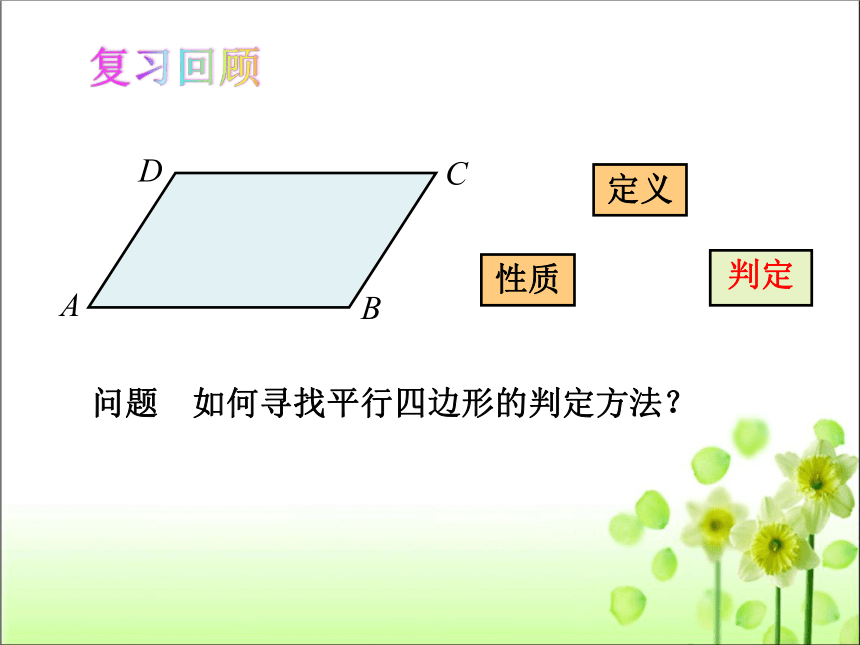
问题 如何寻找平行四边形的判定方法?
复习回顾
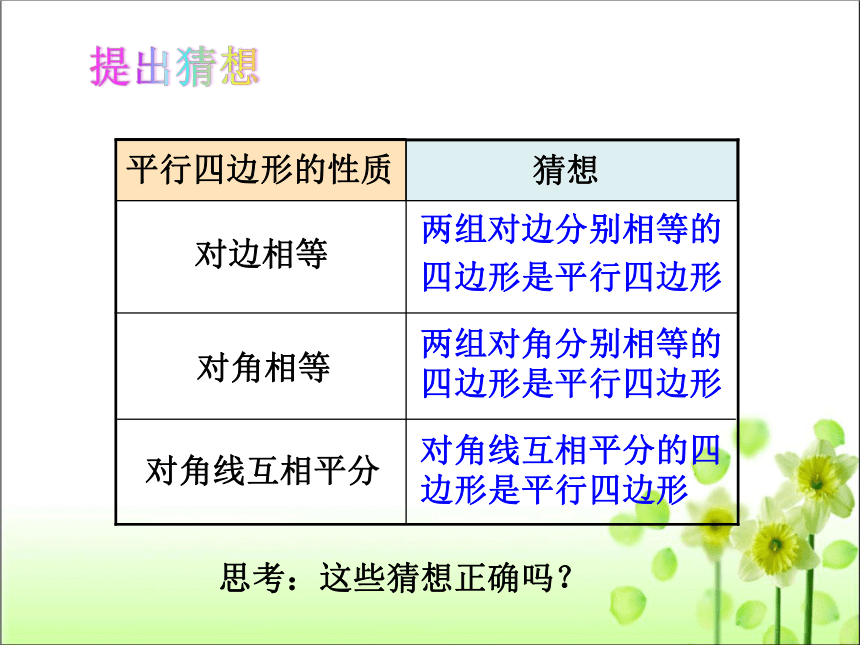
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:这些猜想正确吗?
提出猜想
认真阅读课本第45至46页的内容,完成下面的练习并体验知识点的形成过程.
平行四边形的判定定理
自主研学
1、平行四边形的性质:
(1)从边看:两组对边_______;
两组对边_______;
(2)从角看:两组对角_______;
四组邻角_______;
(3)从对角线看:对角线_______
相互平分
互补
相等
相等
平行
合作探究
2、平行四边形性质的逆命题:
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是_______;
(3)两组对角_______的四边形是_______;
(4)对角线________的四边形是_________。
平行四边形
平行四边形
平行四边形
分别相等
相互平分
猜想:这些逆命题成立吗?
可否成为平行四边形的判别方法?
成立
可以
合作探究
证明:连接BD.
∵ AB=CD,AD=BC,
BD= BD ,
∴ △ABD≌△CDB (sss).
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1
猜想1
D
A
B
C
1
2
3
4
证明猜想
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
证明猜想
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB(SAS).
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
证明猜想
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
归纳小结
例1 如图,口ABCD的对角线AC、BD
相交于点O,E、F是AC上的两点,且
AE=CF。求证:四边形
BFDE是平行四边形。
应用提升
证明:∵ABCD是平行四边形
O是对角线AC、BD交点
∴OA=OC OB=OD
又∵AE=CF ∴OE=OF
∴四边形BFDE是平行四边形
应用提升
思考 你还有其它证明方法吗?写出过程.
证明:∵ABCD是平行四边形
O是对角线AC、BD交点
∴AD=CD ∠DAE=∠BCF
又∵AE=CF ∴△DAE≌△BCF
∴DE=BC
同理△BAE≌△DCF
∴BE=DC
∴四边形BFDE是平行四边形
应用提升
证明:∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF.
1、如图,AB=DC=EF,AD=BC,DE=CF.求证:
AB∥EF.
A
B
C
D
E
F
即学即练
2、如图,口ABCD的对角线AC、BD相交
于点O,E、F分别是OA,OC
的中点。求证:BE=DF。
即学即练
证明:∵ABCD是平行四边形
∴OA=OC
OB=OD
又∵E、F分别是OA、OC的中点。
∴
又∠BOE=∠DOF
∴△BOE≌△DOF
∴BE=DF
即学即练
知识的角度:
平行四边形的判定定理:
定义;
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
课堂小结
过程与方法的角度:
研究图形的一般思路.
解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活应用.
性质
定义
判定
逆向猜想
课堂小结
目标导航二
平形四边形判定的应用
如图,在下列各题中,再添上一个条件使结论成立:
(1)∵ AB∥CD, ,
∴ 四边形ABCD是平行四边形.
(2)∵ AB=CD, ,
∴ 四边形ABCD是平行四边形.
如果只考虑一组对边,
它们满足什么条件时,这
个四边形能成为平行四边
形?
AD∥BC
AD=BC
A
B
C
D
反思延伸
认真阅读课本第46页至47页的内容,完成下面练习并体验知识点的形成过程。
平行四边形的判定定理
平行四边形的判定定理:一组对边平行且相等的四边形是 .
平行四边形
自主研学
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
A
D
B
C
1
2
图一
A
D
B
C
1
2
O
图二
合作探究
证法一:如图一,连接AC,
∵AB∥CD,
∴∠1=∠ .
又AB=CD,AC=CA,
∴△ABC≌ ( )
∴BC= ( )
∴四边形ABCD有两组对边相等,它是平行四边形 。
2
△CDA
SAS
DA
全等三角形的对应边相等
A
D
B
C
1
2
图一
合作探究
证法二:如图二,连接AC,BD交于点O.
∵AB∥CD,
∴∠1=∠ .
又∠AOB=∠COD,AB=CD,
∴△AOB≌ ( )
∴AO= ,BO= .
∴四边形ABCD是平行四边形.
( )
A
D
B
C
1
2
O
图二
2
△COD
ASA
对角线互相平分的四边形是平行四边形
CO
DO
合作探究
1、判断题
⑴相邻的两个角都互补的四边形是平行四边形
( )
⑵两组对角分别相等的四边形是平行四边形 ( )
⑶一组对边平行,另一组对边相等的四边形是平行四边形; ( )
⑷一组对边平行且相等的四边形是平行四边形; ( )
⑸对角线相等的四边形是平行四边形 ( )
⑹对角线互相平分的四边形是平行四边形( )
X
X
即学即练
2、为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
能,一组对边平行且相等的四边形是平行四边形
即学即练
3、如图,AB=DC=EF,AD=BC,DE=CF.图中互相平行的线段有:____________________________ _____.
A
C
D
E
F
B
AB∥CD∥EF;
AD∥BC;
DE∥CF
即学即练
例2 已知:如图, ABCD中,
E、F分别是AD、BC的中点.
求证:四边形EBFD是平行四边形.
分析:证明四边形EBFD的一组对边平行且相等.
证明:∵ 四边形ABCD是平行四边形,
∴ AD∥ ,AD= .
∵ E、F分别是AD、BC的中点,
∴ DE∥BF,且DE=___AD,BF=___BC.
∴ DE= .
∴四边形BEDF是平行四边形( 的四边形是平行四边形).
BC
BC
BF
一组对边平行且相等
应用提升
如图, ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD.E、F为垂足.求证:四边形AFCE是平行四边形.
A
F
E
D
C
B
即学即练
A
F
E
D
C
B
证明:
AE∥CF(垂直于同一直线的两直线平行)
∵四边形ABCD是平行四边形
≌
(一组对边平行且相等的四
边形是平行四边形).
即学即练
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从角考虑 两组对角分别相等的四边形是平行四边形.
从对角线考虑 对角线互相平分的四边形是平行四边形.
从边
考虑
判定一个四边形是平行四边形可从哪些角度思考?
具体有哪些方法?
归纳小结
目标导航三
三角形中位线定理
如图,△ABC中,D,E分别是边AB,AC 的中点,
连接DE. 像DE这样,连接三角形两边中点的线段叫做
三角形的中位线.
看一看,量一量,猜一猜:
DE与BC之间有什么位置关
系和数量关系?
我们在研究平行四边形时,经常采用把平行四边形
转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
反思猜想
认真阅读课本第47页至49页的内容,完成下面练习并体验知识点的形成过程。
知识点一: 三角形中位线的定义
连接___________________
叫做三角形的中位线 .
A
B
C
D
E
三角形两边中点的线段
自主研学
(1)一个三角形的中位线共有几条?
(2)三角形的中位线与中线有什么区别?
答:(1)一个三角形的中位线共有__条;
(2)三角形的中位线与中线的区别主要是线段的端点不同.中位线是____点与____点的连线;中线是_____点与对边_____点的连线.
3
中
中
中
顶
即学即练
知识点二: 三角形的中位线定理
三角形的中位线_____于三角形的第三边,并且等于第三边的_________.
几何叙述:如上图,
∵在△ABC中,AD=BD,AE=CE,
∴DE___BC且DE=_______.
A
B
C
D
E
平行
一半
∥
合作探究
三角形的中位线定理的证明:
如图,点D、E、分别为△ABC的边AB、AC的中点.
求证:DE∥BC且DE= BC.
合作探究
证明:如图,延长DE到点F,使EF=DE,连接CF、CD和AF,
∵AE=_____,DE=_____,
∴四边形ADCF是平行四边形( )
∴CF∥ DA ,又∵AD=BD
∴CF∥ ____ ,
EC
EF
对角线互相平分的四边形是平行四边形
BD
合作探究
∴四边形DBCF是平行四边形.
∴DF∥BC ,
又∵DE= DF,
∴ ∥ 且DE= BC.
温馨提示: “∥”表示平行且相等
DE BC
合作探究
1、在△ABC中,D、E、F分别是AB、BC、CA的中点.以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
A
D
C
B
F
E
解:3个
平行四边形DFCE
平行四边形DFEB
平行四边形DEFA
即学即练
2、如下图,△ABC中,D、E分别是AB、AC的中点,BC=10cm,则DE=______.
3、如右图, △ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,
则∠AED=_____.
5cm
60°
即学即练
4、已知:如图,四边形ABCD中,E、F、G、H分别是AB、OB、OC、AC的中点.
求证:四边形EFGH是平行四边形.
即学即练
证明:∵E、F、G、H分别是
AB、OB、OC、AC的中点,?
∴ED∥BC,ED= BC;
FG∥BC,FG= BC?
∴ED∥FG,ED=FG
∴四边形EFGH是平行四边形。
(一组对边平行且相等的四边形是平行四边形)
即学即练
5、如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC.怎样测出A、B两点间的距离?根据是什么?
A
B
C
解:分别取CA和CB的中点M,N,连接MN,
然后测出MN的长度,则AB=2MN。
理由:三角形的中位线等于第三边的一半。
即学即练
1、三角形中位线的定义:
______________________叫做三角形的中位线 .
2、三角形的中位线与中线的区别:中位线是__________的连线;中线是_________的连线.
3、三角形的中位线定理:三角形的中位线____于三角形的第三边,并且等于第三边的____.
连接三角形两边中点的线段
中点与中点
顶点与中点
平行
一半
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
无所求则无所获。
——华罗庚
18.1.2 平等四边形的判定
人教版八年级数学 下册
目标导航
1.探究平行四边形的判定方法及三角形中位线的概念、定理。
2. 能利用平行四边形的判定方
法及三角形中位线概念和定理解决一些实际问题。
目标导航一
平形四边形的判定
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,邻角互补,对角线互相平分.
?
判定
性质
定义
D
A
B
C
复习回顾
判定
性质
定义
D
A
B
C
问题 如何寻找平行四边形的判定方法?
复习回顾
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:这些猜想正确吗?
提出猜想
认真阅读课本第45至46页的内容,完成下面的练习并体验知识点的形成过程.
平行四边形的判定定理
自主研学
1、平行四边形的性质:
(1)从边看:两组对边_______;
两组对边_______;
(2)从角看:两组对角_______;
四组邻角_______;
(3)从对角线看:对角线_______
相互平分
互补
相等
相等
平行
合作探究
2、平行四边形性质的逆命题:
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是_______;
(3)两组对角_______的四边形是_______;
(4)对角线________的四边形是_________。
平行四边形
平行四边形
平行四边形
分别相等
相互平分
猜想:这些逆命题成立吗?
可否成为平行四边形的判别方法?
成立
可以
合作探究
证明:连接BD.
∵ AB=CD,AD=BC,
BD= BD ,
∴ △ABD≌△CDB (sss).
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1
猜想1
D
A
B
C
1
2
3
4
证明猜想
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
证明猜想
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB(SAS).
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
证明猜想
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
归纳小结
例1 如图,口ABCD的对角线AC、BD
相交于点O,E、F是AC上的两点,且
AE=CF。求证:四边形
BFDE是平行四边形。
应用提升
证明:∵ABCD是平行四边形
O是对角线AC、BD交点
∴OA=OC OB=OD
又∵AE=CF ∴OE=OF
∴四边形BFDE是平行四边形
应用提升
思考 你还有其它证明方法吗?写出过程.
证明:∵ABCD是平行四边形
O是对角线AC、BD交点
∴AD=CD ∠DAE=∠BCF
又∵AE=CF ∴△DAE≌△BCF
∴DE=BC
同理△BAE≌△DCF
∴BE=DC
∴四边形BFDE是平行四边形
应用提升
证明:∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF.
1、如图,AB=DC=EF,AD=BC,DE=CF.求证:
AB∥EF.
A
B
C
D
E
F
即学即练
2、如图,口ABCD的对角线AC、BD相交
于点O,E、F分别是OA,OC
的中点。求证:BE=DF。
即学即练
证明:∵ABCD是平行四边形
∴OA=OC
OB=OD
又∵E、F分别是OA、OC的中点。
∴
又∠BOE=∠DOF
∴△BOE≌△DOF
∴BE=DF
即学即练
知识的角度:
平行四边形的判定定理:
定义;
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
课堂小结
过程与方法的角度:
研究图形的一般思路.
解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活应用.
性质
定义
判定
逆向猜想
课堂小结
目标导航二
平形四边形判定的应用
如图,在下列各题中,再添上一个条件使结论成立:
(1)∵ AB∥CD, ,
∴ 四边形ABCD是平行四边形.
(2)∵ AB=CD, ,
∴ 四边形ABCD是平行四边形.
如果只考虑一组对边,
它们满足什么条件时,这
个四边形能成为平行四边
形?
AD∥BC
AD=BC
A
B
C
D
反思延伸
认真阅读课本第46页至47页的内容,完成下面练习并体验知识点的形成过程。
平行四边形的判定定理
平行四边形的判定定理:一组对边平行且相等的四边形是 .
平行四边形
自主研学
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
A
D
B
C
1
2
图一
A
D
B
C
1
2
O
图二
合作探究
证法一:如图一,连接AC,
∵AB∥CD,
∴∠1=∠ .
又AB=CD,AC=CA,
∴△ABC≌ ( )
∴BC= ( )
∴四边形ABCD有两组对边相等,它是平行四边形 。
2
△CDA
SAS
DA
全等三角形的对应边相等
A
D
B
C
1
2
图一
合作探究
证法二:如图二,连接AC,BD交于点O.
∵AB∥CD,
∴∠1=∠ .
又∠AOB=∠COD,AB=CD,
∴△AOB≌ ( )
∴AO= ,BO= .
∴四边形ABCD是平行四边形.
( )
A
D
B
C
1
2
O
图二
2
△COD
ASA
对角线互相平分的四边形是平行四边形
CO
DO
合作探究
1、判断题
⑴相邻的两个角都互补的四边形是平行四边形
( )
⑵两组对角分别相等的四边形是平行四边形 ( )
⑶一组对边平行,另一组对边相等的四边形是平行四边形; ( )
⑷一组对边平行且相等的四边形是平行四边形; ( )
⑸对角线相等的四边形是平行四边形 ( )
⑹对角线互相平分的四边形是平行四边形( )
X
X
即学即练
2、为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
能,一组对边平行且相等的四边形是平行四边形
即学即练
3、如图,AB=DC=EF,AD=BC,DE=CF.图中互相平行的线段有:____________________________ _____.
A
C
D
E
F
B
AB∥CD∥EF;
AD∥BC;
DE∥CF
即学即练
例2 已知:如图, ABCD中,
E、F分别是AD、BC的中点.
求证:四边形EBFD是平行四边形.
分析:证明四边形EBFD的一组对边平行且相等.
证明:∵ 四边形ABCD是平行四边形,
∴ AD∥ ,AD= .
∵ E、F分别是AD、BC的中点,
∴ DE∥BF,且DE=___AD,BF=___BC.
∴ DE= .
∴四边形BEDF是平行四边形( 的四边形是平行四边形).
BC
BC
BF
一组对边平行且相等
应用提升
如图, ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD.E、F为垂足.求证:四边形AFCE是平行四边形.
A
F
E
D
C
B
即学即练
A
F
E
D
C
B
证明:
AE∥CF(垂直于同一直线的两直线平行)
∵四边形ABCD是平行四边形
≌
(一组对边平行且相等的四
边形是平行四边形).
即学即练
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从角考虑 两组对角分别相等的四边形是平行四边形.
从对角线考虑 对角线互相平分的四边形是平行四边形.
从边
考虑
判定一个四边形是平行四边形可从哪些角度思考?
具体有哪些方法?
归纳小结
目标导航三
三角形中位线定理
如图,△ABC中,D,E分别是边AB,AC 的中点,
连接DE. 像DE这样,连接三角形两边中点的线段叫做
三角形的中位线.
看一看,量一量,猜一猜:
DE与BC之间有什么位置关
系和数量关系?
我们在研究平行四边形时,经常采用把平行四边形
转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
反思猜想
认真阅读课本第47页至49页的内容,完成下面练习并体验知识点的形成过程。
知识点一: 三角形中位线的定义
连接___________________
叫做三角形的中位线 .
A
B
C
D
E
三角形两边中点的线段
自主研学
(1)一个三角形的中位线共有几条?
(2)三角形的中位线与中线有什么区别?
答:(1)一个三角形的中位线共有__条;
(2)三角形的中位线与中线的区别主要是线段的端点不同.中位线是____点与____点的连线;中线是_____点与对边_____点的连线.
3
中
中
中
顶
即学即练
知识点二: 三角形的中位线定理
三角形的中位线_____于三角形的第三边,并且等于第三边的_________.
几何叙述:如上图,
∵在△ABC中,AD=BD,AE=CE,
∴DE___BC且DE=_______.
A
B
C
D
E
平行
一半
∥
合作探究
三角形的中位线定理的证明:
如图,点D、E、分别为△ABC的边AB、AC的中点.
求证:DE∥BC且DE= BC.
合作探究
证明:如图,延长DE到点F,使EF=DE,连接CF、CD和AF,
∵AE=_____,DE=_____,
∴四边形ADCF是平行四边形( )
∴CF∥ DA ,又∵AD=BD
∴CF∥ ____ ,
EC
EF
对角线互相平分的四边形是平行四边形
BD
合作探究
∴四边形DBCF是平行四边形.
∴DF∥BC ,
又∵DE= DF,
∴ ∥ 且DE= BC.
温馨提示: “∥”表示平行且相等
DE BC
合作探究
1、在△ABC中,D、E、F分别是AB、BC、CA的中点.以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
A
D
C
B
F
E
解:3个
平行四边形DFCE
平行四边形DFEB
平行四边形DEFA
即学即练
2、如下图,△ABC中,D、E分别是AB、AC的中点,BC=10cm,则DE=______.
3、如右图, △ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,
则∠AED=_____.
5cm
60°
即学即练
4、已知:如图,四边形ABCD中,E、F、G、H分别是AB、OB、OC、AC的中点.
求证:四边形EFGH是平行四边形.
即学即练
证明:∵E、F、G、H分别是
AB、OB、OC、AC的中点,?
∴ED∥BC,ED= BC;
FG∥BC,FG= BC?
∴ED∥FG,ED=FG
∴四边形EFGH是平行四边形。
(一组对边平行且相等的四边形是平行四边形)
即学即练
5、如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC.怎样测出A、B两点间的距离?根据是什么?
A
B
C
解:分别取CA和CB的中点M,N,连接MN,
然后测出MN的长度,则AB=2MN。
理由:三角形的中位线等于第三边的一半。
即学即练
1、三角形中位线的定义:
______________________叫做三角形的中位线 .
2、三角形的中位线与中线的区别:中位线是__________的连线;中线是_________的连线.
3、三角形的中位线定理:三角形的中位线____于三角形的第三边,并且等于第三边的____.
连接三角形两边中点的线段
中点与中点
顶点与中点
平行
一半
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
