人教版八年级数学 下册 18.2.1 矩形 课件(2课时,共44张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 18.2.1 矩形 课件(2课时,共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 15:21:17 | ||
图片预览








文档简介
(共44张PPT)
强者能同命运的风暴抗争。
—— 爱迪生
18.2.1 矩形
人教版八年级数学 下册
目标导航
1.归纳矩形的概念,明确矩形与平行四边形的区别与联系;
2.探索矩形的性质与判定,会用矩形的性质及判定解决简单的问题;
3.探索“直角三角形斜边上的中线等于斜边的一半”这个性质。
目标导航一
矩形的概念和性质
1、平行四边形的性质有:平行四边形的对边_________;对角_______;邻角___ ;对角线___________.
2、平行四边形的判定方法有:
两组对边____________
两组对边____________
一组对边____________ 的四边形是
平行四边形
两组对角____________
对角线______________
平行且相等
相等
互补
相互平分
分别平行
分别相等
平行且相等
分别相等
相互平分
知识回顾
独木桥
当独木桥静止时,平行四边形ABCD中有一个
角成直角,此时平行四边形ABCD是什么图形?
有一个角是直角
的平行四边形叫做矩
形.
小学中学习过的
长方形是矩形吗?正
方形是矩形吗?
A
B
C
D
知识回顾
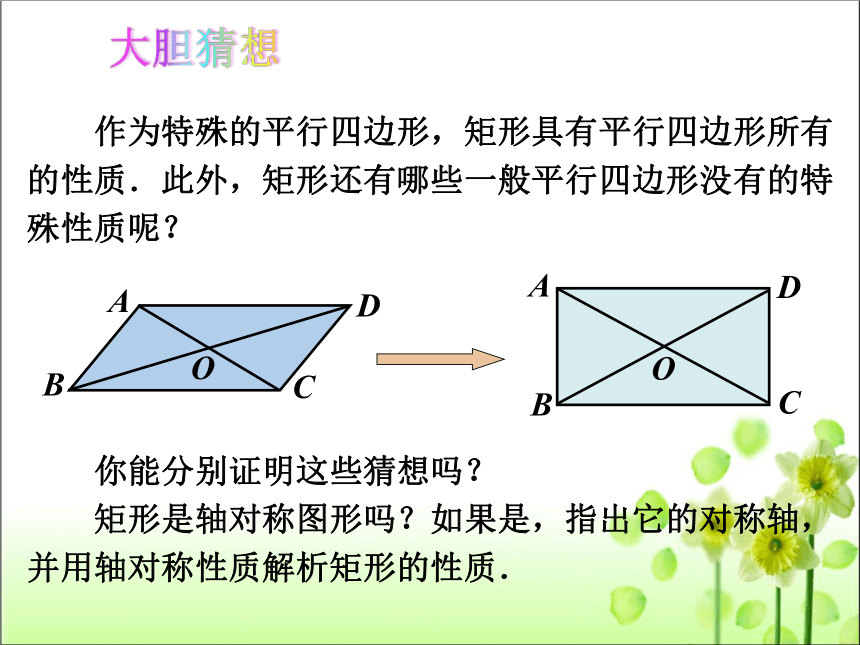
你能分别证明这些猜想吗?
矩形是轴对称图形吗?如果是,指出它的对称轴,
并用轴对称性质解析矩形的性质.
作为特殊的平行四边形,矩形具有平行四边形所有
的性质.此外,矩形还有哪些一般平行四边形没有的特
殊性质呢?
B
C
D
A
O
O
B
C
D
A
大胆猜想
A
B
C
D
O
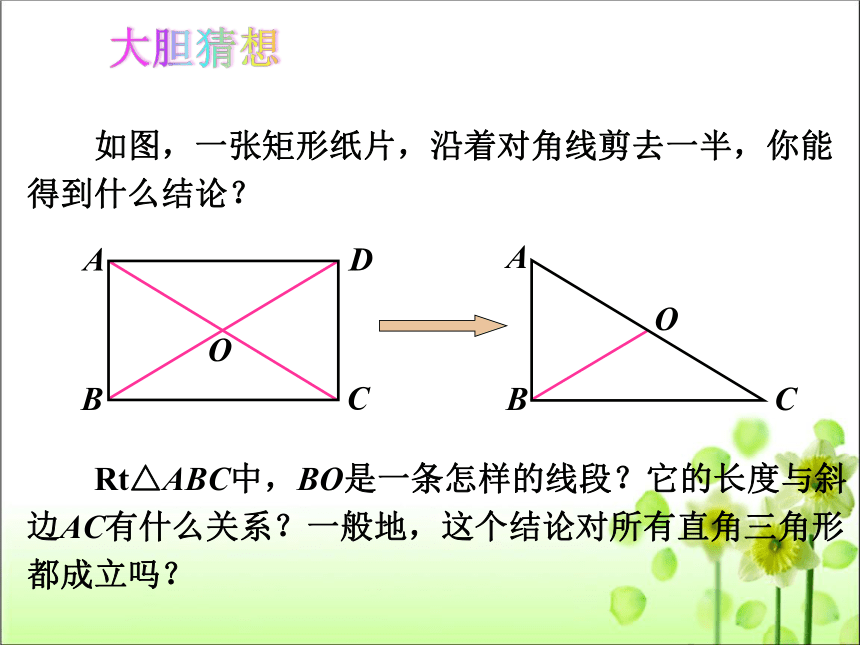
如图,一张矩形纸片,沿着对角线剪去一半,你能
得到什么结论?
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?它的长度与斜
边AC有什么关系?一般地,这个结论对所有直角三角形
都成立吗?
大胆猜想
认真阅读课本第52页至53页的内容,完成下面练习并体验知识点的形成过程。
自主研学
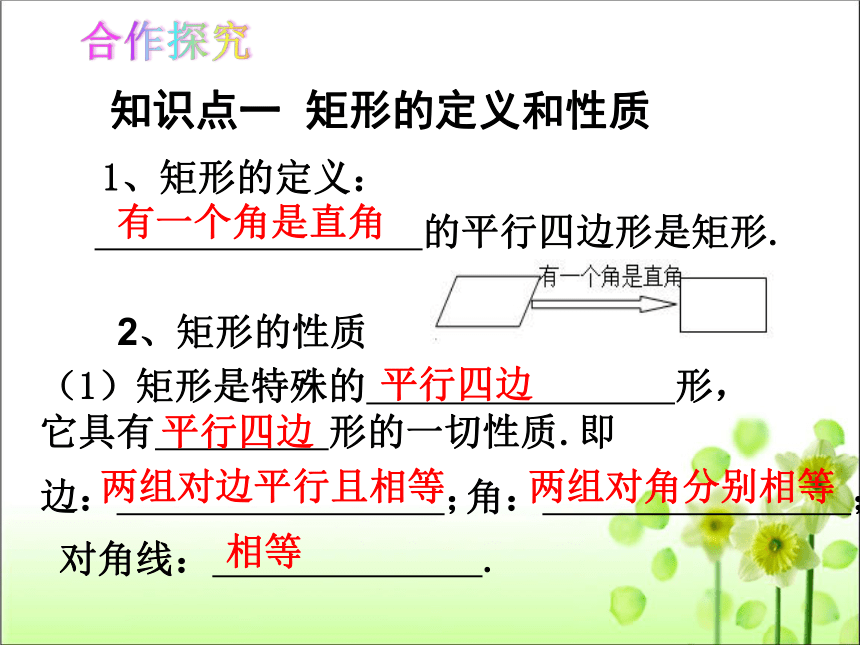
知识点一 矩形的定义和性质
1、矩形的定义:
的平行四边形是矩形.
2、矩形的性质
(1)矩形是特殊的 形,它具有 形的一切性质.即
边: ;
角: ;
对角线: .
有一个角是直角
平行四边
平行四边
两组对边平行且相等
两组对角分别相等
相等
合作探究
(2)矩形还有以下特殊性质:
① ;② .
四个角都是直角
两条对角线相等
合作探究
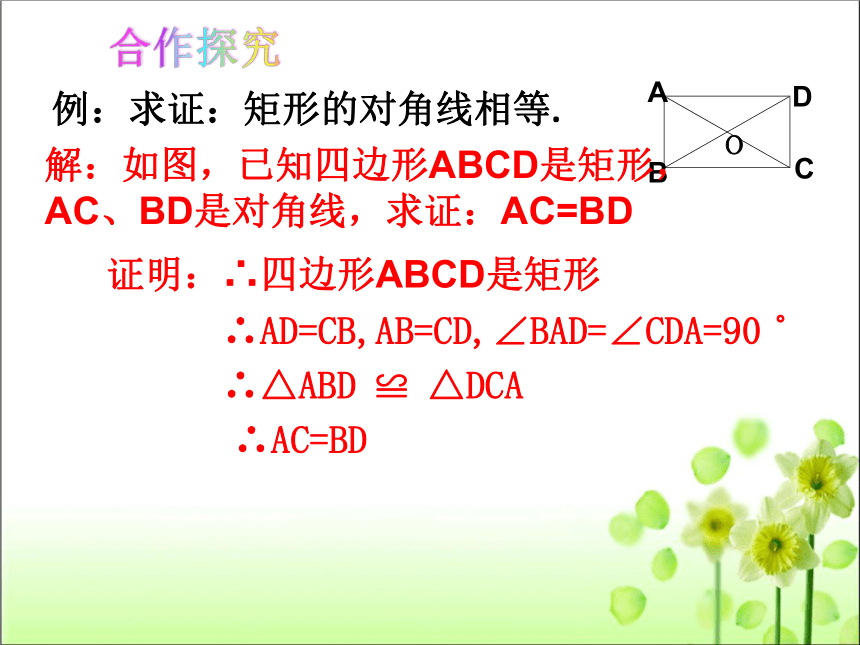
例:求证:矩形的对角线相等.
O
A
B
D
C
解:如图,已知四边形ABCD是矩形,AC、BD是对角线,求证:AC=BD
证明:∴四边形ABCD是矩形
∴AD=CB,AB=CD,∠BAD=∠CDA=90 ?
∴△ABD
△DCA
∴AC=BD
≌
合作探究
1、矩形两条对角线把矩形分成 个等腰三角形.
2、矩形具有而平行四边形不一定具有的性质是 (填代号)
①对边平行且相等;
②对角线互相平分;
③对角相等;
④对角线相等;
⑤4个角都是90°;
⑥轴对称图形
4
④⑤⑥
即学即练
知识点二 矩形性质的应用
如图,在矩形ABCD中,对角线AC,BD相交于点O.
O
A
B
D
C
根据矩形的性质,
AO= = = = =
.
由此我们得到直角三角形的一个性质:
直角三角形斜边上的中线 ___ 斜边的
.
CO
BD
BO
DO
等于
一半
合作探究
几何叙述:
如图∵Rt△ABC中,∠C=90?,CD是AB边上的中线
∴CD= AB
合作探究
例1 如图,矩形ABCD的对角线AC、BD相交于点O, ∠AOB= 60°,AB=4 ,求矩形对角线的长.
O
A
B
D
C
解:∵四边形ABCD是矩形,
∴AC与BD 且 .
∴OA=OB
又∠AOB= 60°,
∴△OAB是 三角形.
∴OA=OB= .
∴AC=BD=2 = .
相等
相互平分
等边
AB
AB
8
合作探究
1、矩形的面积为48,一条边长为6,则矩形的另一边长为 ,对角线为 .
2、矩形是轴对称图形吗?如果是,它有几条对称轴?
3、一个矩形的一条对角线长为8,两条对角线的一个交角为120°.求这个矩形的边长(结果保留小数点后两位).
8
10
答:是,2条对称轴
答:两边长分别是4和6.93
即学即练
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两
条对称轴.
矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
课堂小结
目标导航二
矩形的判定
矩形的定义
有一个角是直角的平行四边形
矩形和四边形的关系
四边形
平行四边形
矩形
知识回顾
矩形的性质
矩形具有平行四边形的所有性质。
矩形的四个角都是90度
矩形的对角线相等
A
B
C
D
边:
角
对角线
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
4.两组对角分别相等的四边形是平行四边形
5.对角线互相平分的四边形是平行四边形
平行四边形的判定方法
你知道矩形的判定方法吗?
认真阅读课本第54至55页的内容,完成下面练习并体验知识点的形成过程。
自主研学
你知道如何判定一个平行四边形是矩形吗?
定义判定:
有一个角是直角的平行四边形是矩形。(方法一)
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
∵
∴
(已知)
(矩形的定义)
几何语言:
合作探究
情境一:李芳同学用四步画出了一个四边形,她的画法是“边——直角、边——直角、边——直角、边”这样,她说这就是一个矩形,她的判断对吗?为什么?
猜想:
你能证明上述结论吗?
有三个角是直角的四边形是矩形 。
合作探究
证明:∵∠A+∠B+∠C+∠D= __ ,
又∵∠A=∠B=∠C= ,
∴∠D=______,
∴四边形ABCD是平行四边形.
(两组对角分别________的四边形是平行四边形)
∴四边形ABCD是 _ .(有一个角是______
的平行四边形是_______)
相等
矩形
直角
矩形
合作探究
矩形的判定方法:
有三个角是直角的四边形是矩形
A
B
C
D
∵ ∠A=∠B=∠C=90°(已知)
∴四边形ABCD是矩形(有三个角是直角的四边形是矩形 )
几何语言:
合作探究
情境二:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:
对角线相等的平行四边形是矩形 。
合作探究
命题:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
合作探究
证明
∴ AB=CD, BC=BC(平行四边形对边相等)
∴ △ABC≌ △DCB(SSS)
∵ 四边形ABCD是平行四边(已知)
在 △ABC和△DCB中
AB=CD (已证)
BC=BC (已证)
AC=BD (已知)
∴ ∠ABC=∠DCB(全等三角形对应边相等)
又∵ ∠ABC+∠DCB=180°(平行四边形邻角互补)
∴ ∠ABC=90°(等式的性质)
又∵ 四边形ABCD是平行四边形(已知)
∴四边形ABCD是矩形(矩形的定义)
A
B
C
D
合作探究
对角线相等的平行四边形是矩形
矩形的判定方法:
几何语言:
∵ AC=BD,四边形ABCD是平行四边形 (已知)
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形 )
A
B
C
D
O
合作探究
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
矩形的判定口诀:
任意一个四边形,
三个直角定矩形。
对于平行四边形,
一个直角即可定,
对线相等也矩形。
合作探究
判断正误:
(1)有一个角是直角的四边形是矩形. ( )
(2)对角线相等的四边形 是矩形. ( )
(3)对角线互相平分且相等的四边形是
矩形. ( )
(4)四个角都相等的四边形是矩形. ( )
(5)一组邻角相等的平行四边形是矩
形. ( )
(6)对角互补的平行四边形是矩形. ( )
√
×
×
√
√
√
即学即练
1、如图,口ABCD对角线AC、BD交于点O,△OAB是等边三角形,且AB=4.求口ABCD面积.
解:∵△OAB是等边三角形且四边形ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB=60° ∴∠AOD=120°
又AO=DO ∴∠ADC=90°
∴四边形ABCD是矩形
AC=8 ,DC=4, AD=
∴平行四边形ABCD面积为
O
合作探究
2、如图AC,BD是矩形ABCD的两条结角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.
证明:∵ABCD是矩形,
∴OA=OC,OB=OD
OE=OA-AE,OG=OC-CG
∵AE=CG
∴OE=OG
OF=OB-OD,OH=OD-DH
合作探究
∵ABCD是矩形,
∴AC=BD
EG=AC-AE-CG
FH=BD-BF-DH
∴EG=FH
∴平行四边形EFGH是矩形
∵BF=DH
∴OF=OH
∴四边形EFGH是平行四边形
合作探究
C
1、下列四边形中不是矩形的是( )
A、有三个角是直角的四边形是矩形
B、四个角都相等的四边形
C、一组对边平行且对角相等的四边形
D、对角线相等且互相平分的四边形
2、如果E、F、G、H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是( )
A、一组对边平行而另一组对边不平行
B、对角线相等
C、对角线互相垂直
D、对角线相等互相平分
C
即学即练
1、矩形的判定定理:
(1)(定义)________________________________;
(2)_____________________________________;
(3)__________________________________.
2、矩形判定定理的应用.
有一个角是直角的平行四边形是矩形
对角线互相平分且相等的平行四边形是矩形
有三个角是直角的四边形是矩形
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
强者能同命运的风暴抗争。
—— 爱迪生
18.2.1 矩形
人教版八年级数学 下册
目标导航
1.归纳矩形的概念,明确矩形与平行四边形的区别与联系;
2.探索矩形的性质与判定,会用矩形的性质及判定解决简单的问题;
3.探索“直角三角形斜边上的中线等于斜边的一半”这个性质。
目标导航一
矩形的概念和性质
1、平行四边形的性质有:平行四边形的对边_________;对角_______;邻角___ ;对角线___________.
2、平行四边形的判定方法有:
两组对边____________
两组对边____________
一组对边____________ 的四边形是
平行四边形
两组对角____________
对角线______________
平行且相等
相等
互补
相互平分
分别平行
分别相等
平行且相等
分别相等
相互平分
知识回顾
独木桥
当独木桥静止时,平行四边形ABCD中有一个
角成直角,此时平行四边形ABCD是什么图形?
有一个角是直角
的平行四边形叫做矩
形.
小学中学习过的
长方形是矩形吗?正
方形是矩形吗?
A
B
C
D
知识回顾
你能分别证明这些猜想吗?
矩形是轴对称图形吗?如果是,指出它的对称轴,
并用轴对称性质解析矩形的性质.
作为特殊的平行四边形,矩形具有平行四边形所有
的性质.此外,矩形还有哪些一般平行四边形没有的特
殊性质呢?
B
C
D
A
O
O
B
C
D
A
大胆猜想
A
B
C
D
O
如图,一张矩形纸片,沿着对角线剪去一半,你能
得到什么结论?
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?它的长度与斜
边AC有什么关系?一般地,这个结论对所有直角三角形
都成立吗?
大胆猜想
认真阅读课本第52页至53页的内容,完成下面练习并体验知识点的形成过程。
自主研学
知识点一 矩形的定义和性质
1、矩形的定义:
的平行四边形是矩形.
2、矩形的性质
(1)矩形是特殊的 形,它具有 形的一切性质.即
边: ;
角: ;
对角线: .
有一个角是直角
平行四边
平行四边
两组对边平行且相等
两组对角分别相等
相等
合作探究
(2)矩形还有以下特殊性质:
① ;② .
四个角都是直角
两条对角线相等
合作探究
例:求证:矩形的对角线相等.
O
A
B
D
C
解:如图,已知四边形ABCD是矩形,AC、BD是对角线,求证:AC=BD
证明:∴四边形ABCD是矩形
∴AD=CB,AB=CD,∠BAD=∠CDA=90 ?
∴△ABD
△DCA
∴AC=BD
≌
合作探究
1、矩形两条对角线把矩形分成 个等腰三角形.
2、矩形具有而平行四边形不一定具有的性质是 (填代号)
①对边平行且相等;
②对角线互相平分;
③对角相等;
④对角线相等;
⑤4个角都是90°;
⑥轴对称图形
4
④⑤⑥
即学即练
知识点二 矩形性质的应用
如图,在矩形ABCD中,对角线AC,BD相交于点O.
O
A
B
D
C
根据矩形的性质,
AO= = = = =
.
由此我们得到直角三角形的一个性质:
直角三角形斜边上的中线 ___ 斜边的
.
CO
BD
BO
DO
等于
一半
合作探究
几何叙述:
如图∵Rt△ABC中,∠C=90?,CD是AB边上的中线
∴CD= AB
合作探究
例1 如图,矩形ABCD的对角线AC、BD相交于点O, ∠AOB= 60°,AB=4 ,求矩形对角线的长.
O
A
B
D
C
解:∵四边形ABCD是矩形,
∴AC与BD 且 .
∴OA=OB
又∠AOB= 60°,
∴△OAB是 三角形.
∴OA=OB= .
∴AC=BD=2 = .
相等
相互平分
等边
AB
AB
8
合作探究
1、矩形的面积为48,一条边长为6,则矩形的另一边长为 ,对角线为 .
2、矩形是轴对称图形吗?如果是,它有几条对称轴?
3、一个矩形的一条对角线长为8,两条对角线的一个交角为120°.求这个矩形的边长(结果保留小数点后两位).
8
10
答:是,2条对称轴
答:两边长分别是4和6.93
即学即练
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两
条对称轴.
矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
课堂小结
目标导航二
矩形的判定
矩形的定义
有一个角是直角的平行四边形
矩形和四边形的关系
四边形
平行四边形
矩形
知识回顾
矩形的性质
矩形具有平行四边形的所有性质。
矩形的四个角都是90度
矩形的对角线相等
A
B
C
D
边:
角
对角线
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
4.两组对角分别相等的四边形是平行四边形
5.对角线互相平分的四边形是平行四边形
平行四边形的判定方法
你知道矩形的判定方法吗?
认真阅读课本第54至55页的内容,完成下面练习并体验知识点的形成过程。
自主研学
你知道如何判定一个平行四边形是矩形吗?
定义判定:
有一个角是直角的平行四边形是矩形。(方法一)
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
∵
∴
(已知)
(矩形的定义)
几何语言:
合作探究
情境一:李芳同学用四步画出了一个四边形,她的画法是“边——直角、边——直角、边——直角、边”这样,她说这就是一个矩形,她的判断对吗?为什么?
猜想:
你能证明上述结论吗?
有三个角是直角的四边形是矩形 。
合作探究
证明:∵∠A+∠B+∠C+∠D= __ ,
又∵∠A=∠B=∠C= ,
∴∠D=______,
∴四边形ABCD是平行四边形.
(两组对角分别________的四边形是平行四边形)
∴四边形ABCD是 _ .(有一个角是______
的平行四边形是_______)
相等
矩形
直角
矩形
合作探究
矩形的判定方法:
有三个角是直角的四边形是矩形
A
B
C
D
∵ ∠A=∠B=∠C=90°(已知)
∴四边形ABCD是矩形(有三个角是直角的四边形是矩形 )
几何语言:
合作探究
情境二:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:
对角线相等的平行四边形是矩形 。
合作探究
命题:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
合作探究
证明
∴ AB=CD, BC=BC(平行四边形对边相等)
∴ △ABC≌ △DCB(SSS)
∵ 四边形ABCD是平行四边(已知)
在 △ABC和△DCB中
AB=CD (已证)
BC=BC (已证)
AC=BD (已知)
∴ ∠ABC=∠DCB(全等三角形对应边相等)
又∵ ∠ABC+∠DCB=180°(平行四边形邻角互补)
∴ ∠ABC=90°(等式的性质)
又∵ 四边形ABCD是平行四边形(已知)
∴四边形ABCD是矩形(矩形的定义)
A
B
C
D
合作探究
对角线相等的平行四边形是矩形
矩形的判定方法:
几何语言:
∵ AC=BD,四边形ABCD是平行四边形 (已知)
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形 )
A
B
C
D
O
合作探究
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
矩形的判定口诀:
任意一个四边形,
三个直角定矩形。
对于平行四边形,
一个直角即可定,
对线相等也矩形。
合作探究
判断正误:
(1)有一个角是直角的四边形是矩形. ( )
(2)对角线相等的四边形 是矩形. ( )
(3)对角线互相平分且相等的四边形是
矩形. ( )
(4)四个角都相等的四边形是矩形. ( )
(5)一组邻角相等的平行四边形是矩
形. ( )
(6)对角互补的平行四边形是矩形. ( )
√
×
×
√
√
√
即学即练
1、如图,口ABCD对角线AC、BD交于点O,△OAB是等边三角形,且AB=4.求口ABCD面积.
解:∵△OAB是等边三角形且四边形ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB=60° ∴∠AOD=120°
又AO=DO ∴∠ADC=90°
∴四边形ABCD是矩形
AC=8 ,DC=4, AD=
∴平行四边形ABCD面积为
O
合作探究
2、如图AC,BD是矩形ABCD的两条结角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.
证明:∵ABCD是矩形,
∴OA=OC,OB=OD
OE=OA-AE,OG=OC-CG
∵AE=CG
∴OE=OG
OF=OB-OD,OH=OD-DH
合作探究
∵ABCD是矩形,
∴AC=BD
EG=AC-AE-CG
FH=BD-BF-DH
∴EG=FH
∴平行四边形EFGH是矩形
∵BF=DH
∴OF=OH
∴四边形EFGH是平行四边形
合作探究
C
1、下列四边形中不是矩形的是( )
A、有三个角是直角的四边形是矩形
B、四个角都相等的四边形
C、一组对边平行且对角相等的四边形
D、对角线相等且互相平分的四边形
2、如果E、F、G、H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是( )
A、一组对边平行而另一组对边不平行
B、对角线相等
C、对角线互相垂直
D、对角线相等互相平分
C
即学即练
1、矩形的判定定理:
(1)(定义)________________________________;
(2)_____________________________________;
(3)__________________________________.
2、矩形判定定理的应用.
有一个角是直角的平行四边形是矩形
对角线互相平分且相等的平行四边形是矩形
有三个角是直角的四边形是矩形
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
