人教版八年级数学 下册 18.2.2 菱形 课件(2课时,共40张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 18.2.2 菱形 课件(2课时,共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 999.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 15:22:44 | ||
图片预览









文档简介
(共40张PPT)
没有哪门学科能比数学更为清晰地阐明自然界的和谐性。
——卡罗斯
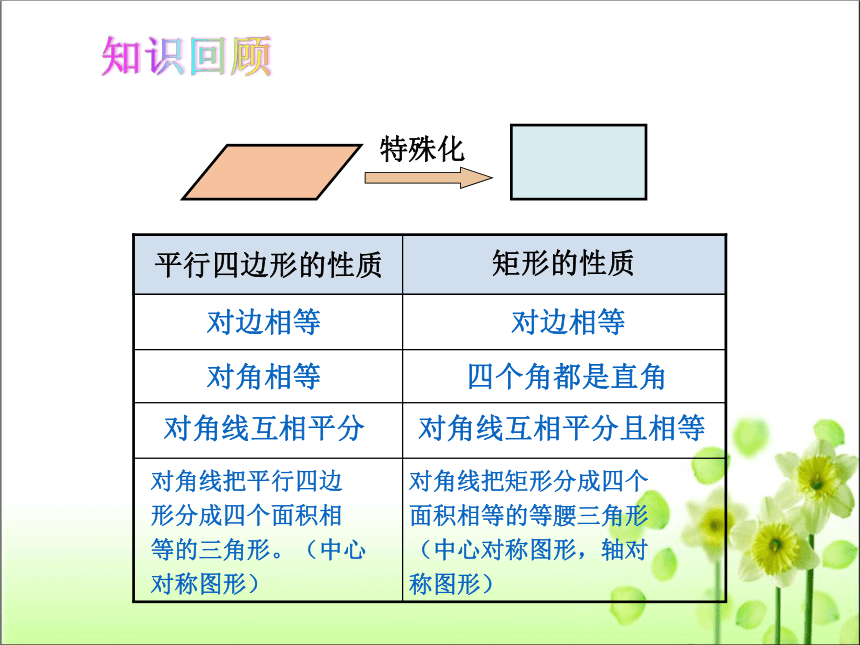
平行四边形的性质
矩形的性质
对边相等
对角相等
对角线互相平分
对角线把平行四边
形分成四个面积相
等的三角形。(中心
对称图形)
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
(中心对称图形,轴对
称图形)
特殊化
知识回顾
平行四边形的角特殊化得到特殊的平行四边形——矩形;
平行四边形的边特殊化,我们得到的特殊的平行四边形是什么,它有什么特征?
大胆猜想
18.2.2 菱 形
人教版八年级数学 下册
目标导航
1.归纳、探究菱形的概念和性质。
2. 探究菱形的三种判定方法。
3、会用菱形的性质和判定定理解决简单的实际问题。
目标导航一
菱形的概念和性质
引导学生读懂数学书课题研究成果配套课件
课件制作:刘集平
下面的图案我们在生活中经常遇到,图中有很多四边形,它们是平行四边形吗?是矩形吗?它们有什么特点?
答:是平行四边形;有矩形;特点:四条边都相等(答案不唯一)
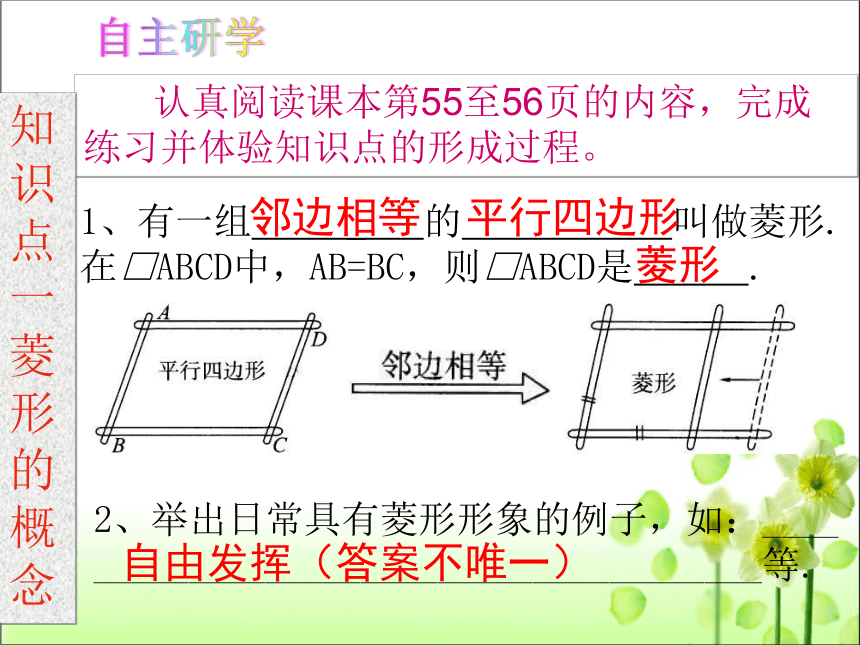
认真阅读课本第55至56页的内容,完成练习并体验知识点的形成过程。
1、有一组 _ 的 叫做菱形.在□ABCD中,AB=BC,则□ABCD是 .
2、举出日常具有菱形形象的例子,如:____
___________________________________等.
邻边相等
平行四边形
菱形
自由发挥(答案不唯一)
自主研学
知识点一菱形的概念
知识点二菱形的性质
1、菱形是 的平行四边形,它具有 的一切性质.
2、菱形的特殊性质.
(1)边:菱形的四条边都 ;
(2)对角线:菱形的两条对角线 ,并且每一条对角线 ;
(3)对称性:菱形是 对称图形, 它的对称轴就是对角线所在的直线.
邻边相等
平行四边形
相等
互相垂直
平分一组对角
轴
合作探究
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
比一比,填写下表:
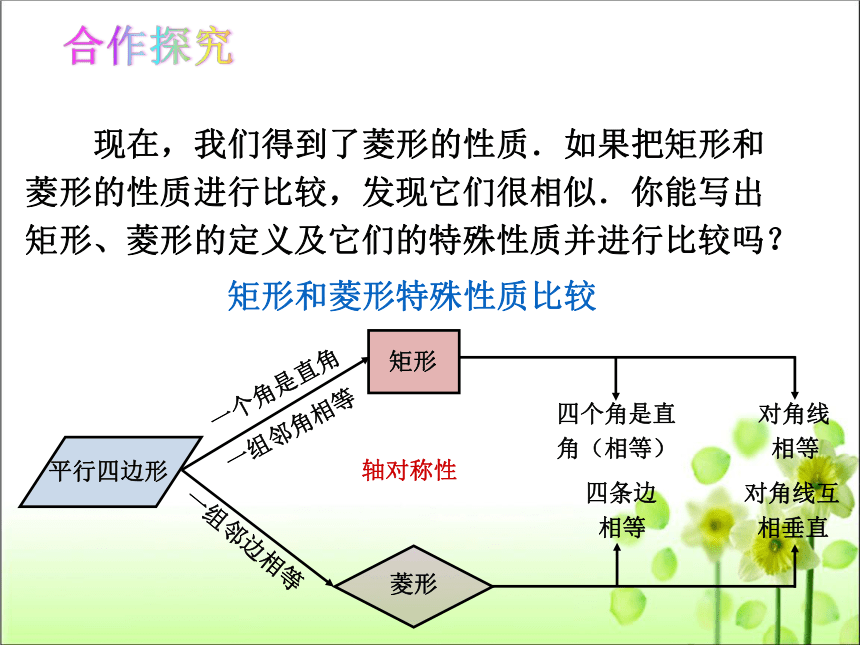
合作探究
现在,我们得到了菱形的性质.如果把矩形和
菱形的性质进行比较,发现它们很相似.你能写出
矩形、菱形的定义及它们的特殊性质并进行比较吗?
矩形和菱形特殊性质比较
平行四边形
矩形
菱形
一个角是直角
一组邻角相等
一组邻边相等
四个角是直
角(相等)
对角线
相等
四条边
相等
对角线互
相垂直
轴对称性
合作探究
1、菱形具有而平行四边形不具有的性质是( )
(A)对角线互相平分
(B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直,每一条对角线平分一组对角
D
即学即练
2、四边形ABCD是菱形,对角线AC、BD相交于点O,且AB=5,AO=4.求AC和BD的长.
O
解:如图所示
由菱形的性质可得:
AC=2 AO=2×4=8
在Rt△OAB中,
即:BD=2BO=2×3=6
即学即练
3、如下图,根据菱形的性质,在菱形ABCD中,
(1)AB= __ = _ = __ ;
(2)AC⊥_ ,且AO= __ ,BO= ;
∠ABO= _ ,∠BCO=_ ,
∠CDO= ,∠DAO= __ .
O
思考:如何证明菱形的性质?写出菱形的对角线互相垂直的证明.
BC
CD
DA
BD
∠ CBO
OC
OD
∠ DCO
∠ ADO
∠ BAO
即学即练
知识点三菱形的面积
例 如图,菱形花坛ABCD的边长为20m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.
求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
合作探究
解:∵花坛ABCD是 ,
∴AC⊥ ,
∠ABO= = ∠ __ = × = .
在Rt△OAB中,AO= = × = ,
(菱形的两条对角线_______________)
BO= = = .
∴花坛的两条小路长 AC=2AO= ,
BD=2BO=____≈__ .
花坛的面积 =4× __
= ·____=_________≈ .
菱形
BD
∠CBO
ABC
60°
30°
AB
20
10
互相垂直平分
20(m)
BD
AC
34.64(m)
346.4(m2)
合作探究
引导学生读懂数学书课题研究成果配套课件
课件制作:刘集平
归纳:
如果菱形ABCD的高为h,则它的面积为
(1)S菱形ABCD = ·____
(2)S菱形ABCD = ·____
AC
BD
AB
h
合作探究
菱形的周长 =4 AB=4×5=20
Rt△OAB中, AB= = =5
(2) = AC·BD= ×8×6=24
AO= AC=4,BO= BD=3
1、已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积
O
解:如图所示,AC=8,BD=6
(1)、由菱形的性质可得:
即学即练
1、有一组 __ 的 叫做菱形.
2、菱形的性质.
(1)具有_____ ____ 的一切性质.
(2)菱形的四条边都 ;
(3)菱形的两条对角线 ,并且每一条对角线 _______ ;
(4)菱形是 对称图形.
3、利用对角线求菱形ABCD的面积:
S菱形ABCD =
·__
邻边相等
平行四边形
平行四边形
相等
垂直
平分一组对角
轴
AC
BD
归纳小结
目标导航二
菱形的判定
答:矩形的对角线相等且每个角是直角。
1、菱形和矩形分别比平行四边形多了哪些性质?
菱形的对角线互相垂直;一组对角平分
对角;每条边都相等。
2、矩形的判定定理:
(1)(定义) _________________ ________;
(2)_____________________________ ___;
(3)_____________________________ ___.
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
回顾反思
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
菱形的
性质
菱形的
判定
C
D
A
B
O
?
回顾反思
认真阅读课本第57至58页的内容,完成练习并体验知识点的形成过程。
自主研学
1、(定义)有一组___________的___________是菱形.
2、对角线_____ _ 的
是菱形.
邻边相等
平行四边形
对角线互相垂直
平行四边形
如何证明这定理?
思考
知识点一 菱形的判定定理
合作探究
已知:如图,在□ABCD中,
AC BD,
求证:□ABCD是 _ .
⊥
证明:∵四边形ABCD是平行四边形,
∴A0= ,
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点
____ __ _)
∴□ABCD是菱形.
菱形
OC
到线段两端点的距离相等
菱形的判定定理
(有一组 的 是菱形)
邻边相等
平行四边形
合作探究
(有一组 的 是菱形)
证明:∵AB=DC,AD=BC,
∴四边形ABCD是_ _____ 形,
(两组对边分别____的四边形是平行四边形)
又∵AB=AD,
∴四边形ABCD是菱形.
已知:如图,在四边形ABCD中,AB=___ =_ __=____.
菱形
BC
CD
AD
3、四条边 _ 的 _ 是菱形.
相等
四边形
求证:四边形ABCD是 __ .
平行四边
相等
知识点一 菱形的判定定理
邻边相等
平行四边形
合作探究
1、判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形.( )
(2)一条对角线垂直另一条对角线的四边形是菱形.( )
(3)对角线互相垂直且平分的四边形是菱形.( )
×
×
√
即学即练
1、判断题,对的画“√”错的画“×”
(4)对角线相等的四边形是菱形.( )
(5)对角线互相平分且邻边相等的四边形是菱形.( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形.( )
√
×
√
合作探究
2、如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
∟
∟
E
F
解:
四边形ABCD是菱形。
过D作DF⊥BC于F
理由如下:过B作BE⊥CD于E,
∵AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
即学即练
∟
∟
E
F
∵BE⊥CD,DF⊥BC
∴∠BEC=∠DFC=900
∵∠BCE=∠DCF ,∠BEC=∠DFC=900,BE=DF
∴BC=CD
∴□ABCD是菱形.
即学即练
?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
归纳小结
即AC BD,
∴□ABCD是菱形.(对角线 的
是菱形.)
∴ 是 三角形(勾股定理的________)
例 如图,ABCD的两条对角线AC、BD相交于点O,且AB=5,AO=4,BO=3.
求证:ABCD是菱形.
证明:∵AB=5,AO=4,BO=3,
∴AB2 AO2 BO2
=
+
直角
逆定理
⊥
互相垂直
菱形的判定定理的应用
平行四边形
合作探究
1、一边长为5cm的平行四边形,两条对角线的长分别为6cm和8cm,那么平行四边形的面积是 .
2、菱形的两条对角线长分别是3和4,则周长和面积分别是 、 。
3、菱形周长为80,一对角线为20,则较小的角的度数为___ _、面积为____ _。
24cm2
10
6
60。
即学即练
4、一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
解:
这是一个特殊的平行四边形
——菱形。
理由如下:如图,在□ABCD中,
AD=9,BD=12,AC=
∵四边形ABCD是平行四边形
∴ OD=6 , OA=
即学即练
∵
即AD2= OA2+OD2
∴ AOD是直角三角形
∴ AC⊥BD
∴□ABCD是菱形。
∴S菱形ABCD=
即学即练
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
课堂小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
没有哪门学科能比数学更为清晰地阐明自然界的和谐性。
——卡罗斯
平行四边形的性质
矩形的性质
对边相等
对角相等
对角线互相平分
对角线把平行四边
形分成四个面积相
等的三角形。(中心
对称图形)
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
(中心对称图形,轴对
称图形)
特殊化
知识回顾
平行四边形的角特殊化得到特殊的平行四边形——矩形;
平行四边形的边特殊化,我们得到的特殊的平行四边形是什么,它有什么特征?
大胆猜想
18.2.2 菱 形
人教版八年级数学 下册
目标导航
1.归纳、探究菱形的概念和性质。
2. 探究菱形的三种判定方法。
3、会用菱形的性质和判定定理解决简单的实际问题。
目标导航一
菱形的概念和性质
引导学生读懂数学书课题研究成果配套课件
课件制作:刘集平
下面的图案我们在生活中经常遇到,图中有很多四边形,它们是平行四边形吗?是矩形吗?它们有什么特点?
答:是平行四边形;有矩形;特点:四条边都相等(答案不唯一)
认真阅读课本第55至56页的内容,完成练习并体验知识点的形成过程。
1、有一组 _ 的 叫做菱形.在□ABCD中,AB=BC,则□ABCD是 .
2、举出日常具有菱形形象的例子,如:____
___________________________________等.
邻边相等
平行四边形
菱形
自由发挥(答案不唯一)
自主研学
知识点一菱形的概念
知识点二菱形的性质
1、菱形是 的平行四边形,它具有 的一切性质.
2、菱形的特殊性质.
(1)边:菱形的四条边都 ;
(2)对角线:菱形的两条对角线 ,并且每一条对角线 ;
(3)对称性:菱形是 对称图形, 它的对称轴就是对角线所在的直线.
邻边相等
平行四边形
相等
互相垂直
平分一组对角
轴
合作探究
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂
直平分,并且每一
条对角线平分一组
对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
比一比,填写下表:
合作探究
现在,我们得到了菱形的性质.如果把矩形和
菱形的性质进行比较,发现它们很相似.你能写出
矩形、菱形的定义及它们的特殊性质并进行比较吗?
矩形和菱形特殊性质比较
平行四边形
矩形
菱形
一个角是直角
一组邻角相等
一组邻边相等
四个角是直
角(相等)
对角线
相等
四条边
相等
对角线互
相垂直
轴对称性
合作探究
1、菱形具有而平行四边形不具有的性质是( )
(A)对角线互相平分
(B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直,每一条对角线平分一组对角
D
即学即练
2、四边形ABCD是菱形,对角线AC、BD相交于点O,且AB=5,AO=4.求AC和BD的长.
O
解:如图所示
由菱形的性质可得:
AC=2 AO=2×4=8
在Rt△OAB中,
即:BD=2BO=2×3=6
即学即练
3、如下图,根据菱形的性质,在菱形ABCD中,
(1)AB= __ = _ = __ ;
(2)AC⊥_ ,且AO= __ ,BO= ;
∠ABO= _ ,∠BCO=_ ,
∠CDO= ,∠DAO= __ .
O
思考:如何证明菱形的性质?写出菱形的对角线互相垂直的证明.
BC
CD
DA
BD
∠ CBO
OC
OD
∠ DCO
∠ ADO
∠ BAO
即学即练
知识点三菱形的面积
例 如图,菱形花坛ABCD的边长为20m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.
求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
合作探究
解:∵花坛ABCD是 ,
∴AC⊥ ,
∠ABO= = ∠ __ = × = .
在Rt△OAB中,AO= = × = ,
(菱形的两条对角线_______________)
BO= = = .
∴花坛的两条小路长 AC=2AO= ,
BD=2BO=____≈__ .
花坛的面积 =4× __
= ·____=_________≈ .
菱形
BD
∠CBO
ABC
60°
30°
AB
20
10
互相垂直平分
20(m)
BD
AC
34.64(m)
346.4(m2)
合作探究
引导学生读懂数学书课题研究成果配套课件
课件制作:刘集平
归纳:
如果菱形ABCD的高为h,则它的面积为
(1)S菱形ABCD = ·____
(2)S菱形ABCD = ·____
AC
BD
AB
h
合作探究
菱形的周长 =4 AB=4×5=20
Rt△OAB中, AB= = =5
(2) = AC·BD= ×8×6=24
AO= AC=4,BO= BD=3
1、已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积
O
解:如图所示,AC=8,BD=6
(1)、由菱形的性质可得:
即学即练
1、有一组 __ 的 叫做菱形.
2、菱形的性质.
(1)具有_____ ____ 的一切性质.
(2)菱形的四条边都 ;
(3)菱形的两条对角线 ,并且每一条对角线 _______ ;
(4)菱形是 对称图形.
3、利用对角线求菱形ABCD的面积:
S菱形ABCD =
·__
邻边相等
平行四边形
平行四边形
相等
垂直
平分一组对角
轴
AC
BD
归纳小结
目标导航二
菱形的判定
答:矩形的对角线相等且每个角是直角。
1、菱形和矩形分别比平行四边形多了哪些性质?
菱形的对角线互相垂直;一组对角平分
对角;每条边都相等。
2、矩形的判定定理:
(1)(定义) _________________ ________;
(2)_____________________________ ___;
(3)_____________________________ ___.
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
回顾反思
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
菱形的
性质
菱形的
判定
C
D
A
B
O
?
回顾反思
认真阅读课本第57至58页的内容,完成练习并体验知识点的形成过程。
自主研学
1、(定义)有一组___________的___________是菱形.
2、对角线_____ _ 的
是菱形.
邻边相等
平行四边形
对角线互相垂直
平行四边形
如何证明这定理?
思考
知识点一 菱形的判定定理
合作探究
已知:如图,在□ABCD中,
AC BD,
求证:□ABCD是 _ .
⊥
证明:∵四边形ABCD是平行四边形,
∴A0= ,
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点
____ __ _)
∴□ABCD是菱形.
菱形
OC
到线段两端点的距离相等
菱形的判定定理
(有一组 的 是菱形)
邻边相等
平行四边形
合作探究
(有一组 的 是菱形)
证明:∵AB=DC,AD=BC,
∴四边形ABCD是_ _____ 形,
(两组对边分别____的四边形是平行四边形)
又∵AB=AD,
∴四边形ABCD是菱形.
已知:如图,在四边形ABCD中,AB=___ =_ __=____.
菱形
BC
CD
AD
3、四条边 _ 的 _ 是菱形.
相等
四边形
求证:四边形ABCD是 __ .
平行四边
相等
知识点一 菱形的判定定理
邻边相等
平行四边形
合作探究
1、判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形.( )
(2)一条对角线垂直另一条对角线的四边形是菱形.( )
(3)对角线互相垂直且平分的四边形是菱形.( )
×
×
√
即学即练
1、判断题,对的画“√”错的画“×”
(4)对角线相等的四边形是菱形.( )
(5)对角线互相平分且邻边相等的四边形是菱形.( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形.( )
√
×
√
合作探究
2、如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
∟
∟
E
F
解:
四边形ABCD是菱形。
过D作DF⊥BC于F
理由如下:过B作BE⊥CD于E,
∵AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
即学即练
∟
∟
E
F
∵BE⊥CD,DF⊥BC
∴∠BEC=∠DFC=900
∵∠BCE=∠DCF ,∠BEC=∠DFC=900,BE=DF
∴BC=CD
∴□ABCD是菱形.
即学即练
?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
归纳小结
即AC BD,
∴□ABCD是菱形.(对角线 的
是菱形.)
∴ 是 三角形(勾股定理的________)
例 如图,ABCD的两条对角线AC、BD相交于点O,且AB=5,AO=4,BO=3.
求证:ABCD是菱形.
证明:∵AB=5,AO=4,BO=3,
∴AB2 AO2 BO2
=
+
直角
逆定理
⊥
互相垂直
菱形的判定定理的应用
平行四边形
合作探究
1、一边长为5cm的平行四边形,两条对角线的长分别为6cm和8cm,那么平行四边形的面积是 .
2、菱形的两条对角线长分别是3和4,则周长和面积分别是 、 。
3、菱形周长为80,一对角线为20,则较小的角的度数为___ _、面积为____ _。
24cm2
10
6
60。
即学即练
4、一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
解:
这是一个特殊的平行四边形
——菱形。
理由如下:如图,在□ABCD中,
AD=9,BD=12,AC=
∵四边形ABCD是平行四边形
∴ OD=6 , OA=
即学即练
∵
即AD2= OA2+OD2
∴ AOD是直角三角形
∴ AC⊥BD
∴□ABCD是菱形。
∴S菱形ABCD=
即学即练
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
课堂小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
