人教版八年级数学 下册 19.2.3 一次函数与方程、不等式 课件(3课时,共73张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 19.2.3 一次函数与方程、不等式 课件(3课时,共73张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1015.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 15:32:42 | ||
图片预览









文档简介
(共73张PPT)
在这个世界上取得成就的人,都
努力去寻找他们想要的机会,如果找
不到机会,他们便自己创造机会。
—— 萧伯纳
19.2.3 一次函数与
方程、不等式
人教版八年级数学 下册
目标导航
1.认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系.会用函数观点解释方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想
目标导航一
一次函数与一元一次方程
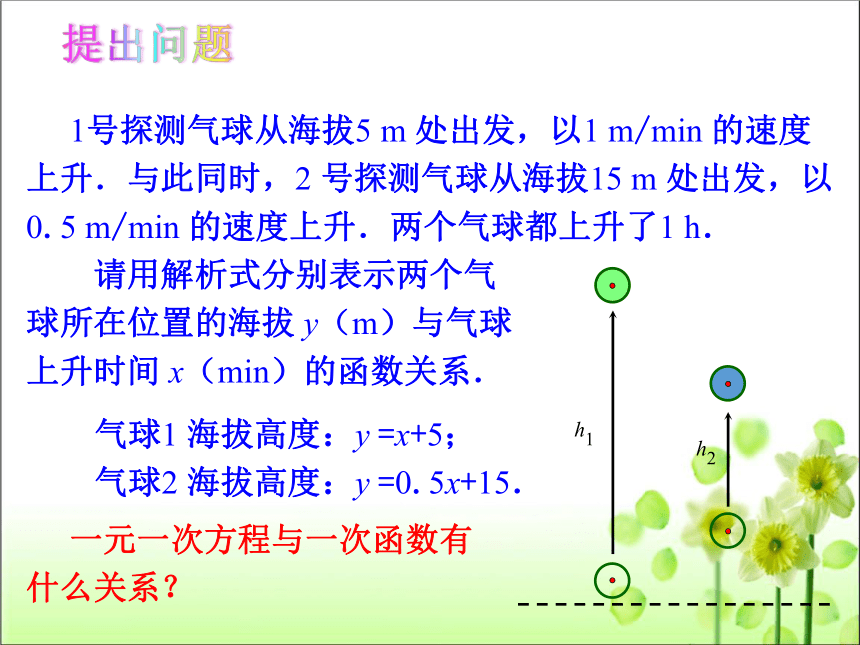
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以
0.5 m/min 的速度上升.两个气球都上升了1 h.
请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
一元一次方程与一次函数有
什么关系?
提出问题
认真阅读课本第96页的内容,完成下面练习并体验知识点的形成过程。
知识点一 函数与一元一次方程
自主研学
(1)解方程:2x+20=0
(2)当x为何值时函数 y=2x+20的值为0?
问题(1)与(2)有什么关系呢?
提出问题
(1)解方程 .
(2)当自变量 x 为何值时,函数y =2x+20 的值为0?
以下两个问题有什么关系?
解:(1) 2x+20=0
(2) 令 y=0 ,即
两个问题实际上是同一个问题.
从“数”上看
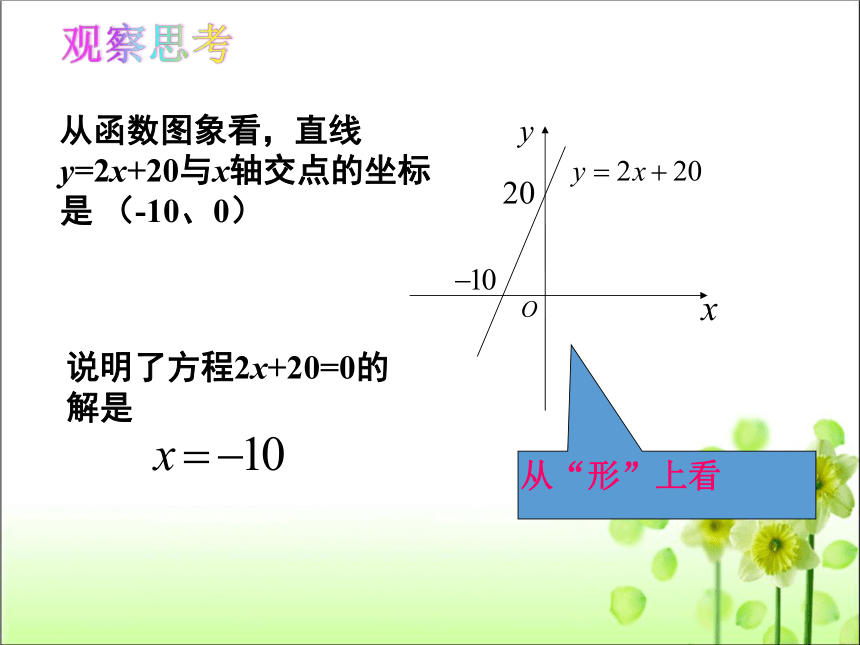
观察思考
从函数图象看,直线y=2x+20与x轴交点的坐标是 (-10、0)
说明了方程2x+20=0的解是
从“形”上看
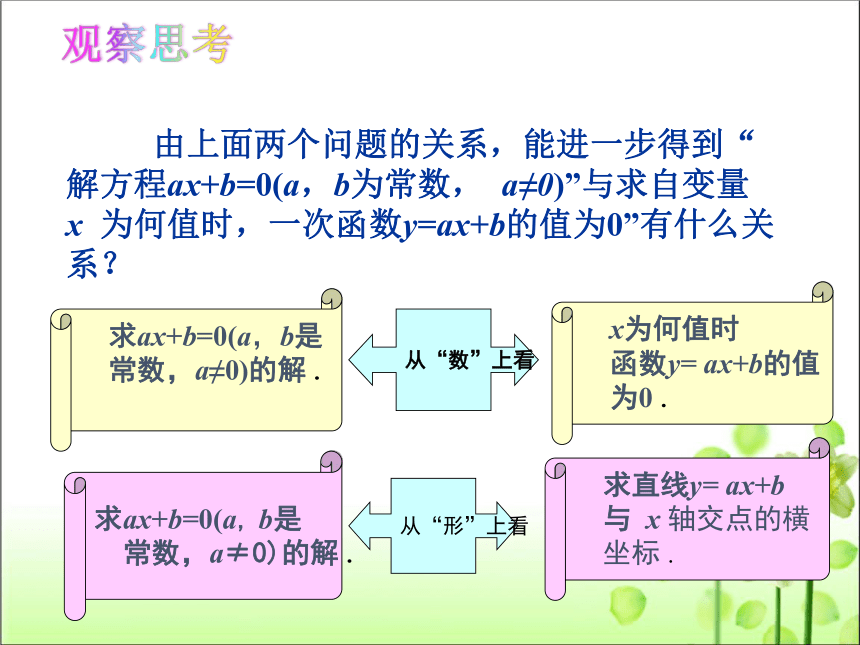
观察思考
求ax+b=0(a,b是
常数,a≠0)的解.
由上面两个问题的关系,能进一步得到“解方程ax+b=0(a,b为常数, a≠0)”与求自变量 x 为何值时,一次函数y=ax+b的值为0”有什么关系?
x为何值时
函数y= ax+b的值
为0.
从“数”上看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b
与 x 轴交点的横
坐标.
从“形”上看
观察思考
序号 一元一次方程问题 一次函数问题
1 解方程 3x-2=0 当x为何值时,
y=3x-2的值为0?
2 解方程 8x-3=0
3 当x为何值时,
y=-7x+2的值为0?
4 解方程 8x-3=2
举一反三
当x为何值时,___________的值为0?
解方程 - 7x+2=0
8x-5=0
y=8x-3
当x为何值时,___________的值为0?
y=8x-5
因为任何一个以x为求知数的一元一次方程都可以变形为 (a≠0)的形式,所以解一元一次方程相当于在某个一次函数 的函数值为 时,
求 __的值.
0
自变量x
归纳小结
3
2
1
2
1
-2
O
x
y
-1
-1
3
例1 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程
ax +b =k 就是求当函
数值为k 时对应的自
变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
合作探究
1、直线 在坐标系中的位置如图,则方程 的解是χ=___
-2
2
x
y
0
-2
2、直线 与轴的交点是(? )
A.(0,-3)???B.(-3,0)????
C.(0,3)??? D.(0,-3)
B
即学即练
3、已知方程ax+b=0的解是-2,下列图像肯定不是直线y=ax+b的是( )
A
B
C
D
B
即学即练
x=2
2
解:由图象可知x+3=0的
解为x= ?3.
3
x
y
0
-3
从“形”上看
析:直线y=x+3的图象与x轴交点坐标为(-3,0 ),这说明方程χ+3=0的解是x=-3)
4、方程 的解是 ,则函数
在自变量 等于 时的函数值是8.
5、根据图象,你能直接说出一元一次方程 的解吗?
即学即练
因为任何一个以为未知数的一元一次方程都可以变形为 的形式,所以解一元一次方程相当于在某个一次函数 的函数值为0时, 求 的值.
自变量x
归纳小结
解一元一次方程ax+b=0 (a ,b为常数)可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,这相当于已知直线y=ax+b,确定它与x轴交点的横坐标的值。
即:
目标导航二
一次函数与一元一次不等式
1.直线 y=ax+b 在坐标系中的位置如图,
则方程 ax+b=0 的解是 x= ____
0
-4
3
x
y
- 4
复习巩固
2、画出一次函数 y=3x+2 的图象。
x 0
y=3x+2 2 0
复习巩固
思考:
问题1与问题2有什么关系?
问题2:
自变量为何值时,函数y=2x-4的值大于0?
问题1:解不等式2x-4>0
提出问题
知识点 一次函数与一元一次不等式
认真阅读课本第96至97页的内容,完成下面练习并体验知识点的形成过程。
自主研学
1、观察下面3个不等式有什么共同点与不同点?
(1) >2;
(2) <0;
(3) <-1
合作探究
3个不等式相同的特点是:不等号左边都是_______;不同点是:不等号及不等号右边分别是____ ,_____,_____。
2
0
-1
合作探究
你能从函数的角度对以上3个不等式 进行解释吗?
解释1:
解这3个不等式相当于在一次函数
的函数值分别为_____、_____ 、 _____时,求自变量的取值范围。
大于2
小于0
小于-1
合作探究
解释2:
在直线 上取纵坐标分别满足大于2、小于0、小于-1的点,看他们的横坐标分别满足什么条件。
当y>2时,则x>0
当y<0时,则x<
当y<-1时,则x<-1
合作探究
结论
因为任何一个以为求知数的一元一次不等式都可以变形为 ax+b>0 或 ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的值 _____或_____时,求自变量x的________。
大于0
小于0
取值范围
合作探究
-2
x
y=3x+6
y
例 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
1、已知函数 y=x-3 ,
当x____时,y>0;当 x____时,y<0。
2、已知一次函数 y=kx+b的图象如图所示,则不等式 kx+b>0的
解集是( )
A.x>-2? B.x<-2
C.x>-1???? D.x<-1
>3
<3
B
即学即练
3、利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
即学即练
4、直线 y=x-1 上的点在 x 轴上方时对应的自变量的范围是( ? )
A. x>1?? B. x≥1 C. x<1?????D. x≤1
5、已知直线 y=2x+k 与 x 轴的交点为 (-2,0),则关于x的不等式 2x+k<0 的解集是 (? )
A. x>-2????B. x≥-2 C. x<-2????D. x≤-2
A
C
即学即练
可以看出,当x<2时这条直线上的点在x轴的下方,
解法一:化简得3x-6<0,画出直线y=3x-6,
即这时y=3x-6<0,所以不等式的解集为x<2
例: 用画函数图象的方法解不等式 5x+4<2x+10
y
x
-6
2
0
Y=3x-6
合作探究
解法二:画出函数 y = 2x+10 y = 5x+4图象
从图中看出:当x <2时
直线 y = 5x +4 在 y = 2x +10的下方
即 5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10 的解集是
x < 2
Y1=5x+4
y
x
0
Y2=2X+10
2
-2
合作探究
1.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x+2的解集是______。
2.当自变量x为何值时,函数y=2x-4的值大于0?
解:由题意,得 2x-4>0
x>2
∴当自变量x>2时,函数y=2x-4的
值大于0
x≥2
即学即练
2、试根据函数y=3x-15的性质或图象,确定取何值时:
(1)y>0; (2)y<0
解:令3x-15=0,解得,x=5
∵函数y=3x-15中k=3>0,
∴y随x的增大而增大,
∴(1)当x>5时,y>0;
(2)当x<5时,y<0。
即学即练
因为任何一个以x为求知数的一元一次不等式都可以变形为____________
_______________ 的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的函数值大于0或小于0时,求自变量x的_________。
ax+b>0 或
ax+b<0(a≠0)
取值范围
归纳小结
一次函数与一元一次不等式的关系
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
目标导航三
一次函数与二元一次方程组
1.直线 y=ax+b 在坐标系中的位置如图,
则方程 ax+b>0 的解是 x ____
x
y
0
3
-4
>- 4
知识回顾
25
15
5
10
20
x
0
y
2、画出一次函数y=x+5与y=0.5x+15的图象。
解:列表,得
x 0 20
y=x+5 5 25
y=0.5x+15 15 25
描点、连线得:
y=0.5x+15
y=x+5
3.上图中两条直线的交点坐标是( , )
20
25
知识回顾
(1)把二元一次方程y-x=1
写成一次函数y=____________的形式
2、你能找出方程的几组解吗?
3、把以这几组解为坐标的点在坐标系上描出来,你发现了什么?
x+1
1、画出一次函数y=x+1的图像
4、以二元一次方程y-x=1的所有解为坐标的点都在一次函数y=x+1的图像上吗?
问题探究
探究
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y=x+1
即: 二元一次方程 (数)
相应的一次函数的图象一条直线 (形)
对应
结论:
以二元一次方程的解为坐标的点都在相应的函数图象上.反过来,
一次函数图象上的点的坐标都是相应的二元一次方程的解.
认真阅读课本第97页的内容,完成下面练习并体验知识点的形成过程。
知识点一 一次函数与二元一次方程组
自主研学
问题:
1号探测气球从海拔5米处出发,以1米/分的速度上升.与此同时 ,2号探测气球从海拔15米处出发,以0.5米/分的速度上升.两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系;
(2)在某个时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
合作探究
分析:
(1) 气球上升时间满足__________。
1号气球的函数解析式为_________;
2号气球的函数解析式为_________ 。
(2) 在某个 时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有__________。 则只需求出x和y的值。
0≤x≤60
y=x+5
y=0.5x+15
相同的y值
合作探究
解:联立方程组:
y=x+5
y=0.5x+15
解二元一次方程组得:
x=_____
y=_____
答:当气球上升 分钟时,两气球都位于海拔 米的高度.
20
25
25
20
合作探究
答:1.一般地,因为每个含有求知数和的二元一次方程组,都可以改写为_______的形式,所以每个这样的方程都对应一个一次函数,于是也对应________。这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解。
思考:
新课引入中函数图象,你能解释两直线的交点坐标(20,25)就是问题3的解吗?
y=kx+b
一条直线
合作探究
从“数”的角度看,解二元一次方程组,相当于求自变量为何值时相应的两个函数值_____,以及这个函数值是多少;
从“形”的角度看,解二元一次方程组,相当于确定________的交点坐标。因此,我们可以用画一次函数图象的方法得到方程组的解。
相等
两条直线
得出结论
1、以方程2x-y=1的解为坐标的点都在
一次函数 ______的图像上。
2、方程组 的解是 ,由此可知一
次函数 与 的图像必有一个交点,
且交点坐标是 。
x-y=4
3x-y=16
y=2x-1
x=6
y=2
y=x+4
y=-3x+16
(6,2)
即学即练
3、根据下列图象,你能说出它表示哪个方程组的解?这个解是什么?
1
1
x
y
o
y=2x-1
y=-3x+4
即学即练
4、方程组 的解是
则函数 与 的交点P的坐标是______
5、一次函数y=3x-4的图象是一条直线,它由无数个点组成的,那么方程3x-y=4 的解有( )
A.1个 B.2个 C.3个 D.无数个
D
即学即练
2x+y=4
2x-3y=12
用图象法解方程组:
①
②
解:
由①得:
由②得:
作出图象:
观察图象得:交点为(3,-2)
∴方程组的解为
x=3
y=-2
x
o
y
y=-2x+4
y=2/3x - 4
合作探究
二元一次方程组的解与以这两个方程所对应的一次函数图象的交点坐标相对应。
由此可得:
二元一次方程组的图象解法.
写函数,作图象,找交点,下结论
合作探究
y
o
x
x-y=0
2x+y=5
作出图象:
观察图象得:交点(1.7,1.7)
∴方程组的解为
x=1.7
y=1.7
精确!
图象法:
你有哪些方法?
解方程组
代数法:
x=5/3
y=5/3
∴方程组的解为
用作图象的方法可以直观地获得问题的结果,但有时却难以准确.为了获得准确的结果,我们一般用代数方法.
近似!
合作探究
y=x
y=-2x+5
例:老师为了教学,需要在家上网查资料。电信公司
提供了两种上网收费方式:
方式 1 :按上网时间以每分钟 0.1 元计费;
方式 2 :月租费 20 元,再按上网时间
以每分钟 0.05 元计费。
请同学们帮老师选择:以何种方式上网更合算?
合作探究
o
y/元
x /分
20
400
200
y1 =0.1x
y 2=0.05x+20
40
30
在同一坐标系中分别画出这两个函数的图像
当 x = 400 时,
y1 = y2
当 x>400 时,
y1 > y2
当 0≤x<400 时,
y1 < y2
y1=0.1x
y2=0.05x+20
解:设上网时间为 x 分,若按方式 1 则收 元;
若按方式 2 则收 元。
y1=0.1x
y2=0.05x+20
由函数图像得:
当 时,y>0,
即选方式 省钱;
当 时,y=0,
即选方式A、B ;
当 时,y<0,
即选方式 省钱;
400
y=-0.05x+20
20
0
y
x
解法2:设上网时间为 x 分,方式 B与方式 A两种计费的差额为
y元,则 y 随 x 变化的函数关系式为 .
化简得 。
在直角坐标系中画出这个函数的图像。
y=(0.05x+20) -0.1x
y=-0.05x +20
0≤x<400
X=400
X>400
A
B
一样
在一元一次方程一章中,我们曾考虑过下面两种移动电话计费方式:
方式一 方式二
月租费 30元/月 0
本地通话费 0.30元/分 0.40元/分
用函数方法解答如何选择计费方式更省钱
方式一费用: y1 = 0.3x + 30
方式二费用: y2 = 0.4x
两种计费差额为 : y = y1-y2 = -0.1x + 30
当 x <300 分时,y>0 ,y1>y2 ,方式二省钱
当 x = 300 分时,y =0 ,y1 =y2 , 方式一方式二一样
当 x > 300分时,y<0 ,y1<y2 ,方式一省钱
300
0
30
x
y
合作探究
方程(组)与函数之的互相联系,从函数的角度可以把它们统一起来,解决问题时,应根据具体情况灵活地把它们结合起来考虑。
归纳小结
1、当自变量取何值时,函数 与
的值相等?这个函数值是多少?
解:由已知可得:
2.5x+ 1 = 5x+ 17,
解得:x=-6.4
则这个函数值y=5×(-6.4)+17=-15
检测目标
解:由题意可得:
当直线y=3x+ 6与χ轴相交时,y=0
即3x+ 6=0, 解得:x= -2,
2、直线 与 轴的交点的横坐标的值是方程 的解,求 的值.
当x= -2 时,2 x (-2) + a =0
解得:a = 4
检测目标
下方
3.若关于x的不等式
的解集为
则一次函数
当
时,图象在
时,图象在x轴______.
x轴_________;当
上方
分析:可以画出函数草图进行解答
检测目标
4.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
x<-2
分析:即求y>-2时x的取值范围
检测目标
5、看图象解不等式
x
o
y=5x-3
2
y=3x+1
7
y
从图中看出,当x>2时,直线y=5x-3上的点在直线y=3x+1上相应点的上方,即5x-3>3x+1,所以不等式的解集为x>2。
检测目标
6、直线y=-x+4和y=2x-5直线的交点坐标是________。
7、一次函数 与 的图象是两条_____的直线,因此 的解的情况是______。
(3,1)
平行
无解
检测目标
8、考虑下面两种移动电话计费方式:
用函数方法解答何时两种计费方式费用相等。
方式一 方式二
月租费(元/月) 30 0
本地通话费
(元/分钟) 0.30 0.40
检测目标
解:设电话费用为y元,通话时间x分钟,则
方式一:
方式二:
y=30+0.3x
y=0.4x
因为函数y=30+0.3x与函数y=0.4x的图象交于点(300,120),因此当通话时间为300分钟时,两种计费方式的费用相等(都是120元)。
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
在这个世界上取得成就的人,都
努力去寻找他们想要的机会,如果找
不到机会,他们便自己创造机会。
—— 萧伯纳
19.2.3 一次函数与
方程、不等式
人教版八年级数学 下册
目标导航
1.认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系.会用函数观点解释方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想
目标导航一
一次函数与一元一次方程
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以
0.5 m/min 的速度上升.两个气球都上升了1 h.
请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
一元一次方程与一次函数有
什么关系?
提出问题
认真阅读课本第96页的内容,完成下面练习并体验知识点的形成过程。
知识点一 函数与一元一次方程
自主研学
(1)解方程:2x+20=0
(2)当x为何值时函数 y=2x+20的值为0?
问题(1)与(2)有什么关系呢?
提出问题
(1)解方程 .
(2)当自变量 x 为何值时,函数y =2x+20 的值为0?
以下两个问题有什么关系?
解:(1) 2x+20=0
(2) 令 y=0 ,即
两个问题实际上是同一个问题.
从“数”上看
观察思考
从函数图象看,直线y=2x+20与x轴交点的坐标是 (-10、0)
说明了方程2x+20=0的解是
从“形”上看
观察思考
求ax+b=0(a,b是
常数,a≠0)的解.
由上面两个问题的关系,能进一步得到“解方程ax+b=0(a,b为常数, a≠0)”与求自变量 x 为何值时,一次函数y=ax+b的值为0”有什么关系?
x为何值时
函数y= ax+b的值
为0.
从“数”上看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b
与 x 轴交点的横
坐标.
从“形”上看
观察思考
序号 一元一次方程问题 一次函数问题
1 解方程 3x-2=0 当x为何值时,
y=3x-2的值为0?
2 解方程 8x-3=0
3 当x为何值时,
y=-7x+2的值为0?
4 解方程 8x-3=2
举一反三
当x为何值时,___________的值为0?
解方程 - 7x+2=0
8x-5=0
y=8x-3
当x为何值时,___________的值为0?
y=8x-5
因为任何一个以x为求知数的一元一次方程都可以变形为 (a≠0)的形式,所以解一元一次方程相当于在某个一次函数 的函数值为 时,
求 __的值.
0
自变量x
归纳小结
3
2
1
2
1
-2
O
x
y
-1
-1
3
例1 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程
ax +b =k 就是求当函
数值为k 时对应的自
变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
合作探究
1、直线 在坐标系中的位置如图,则方程 的解是χ=___
-2
2
x
y
0
-2
2、直线 与轴的交点是(? )
A.(0,-3)???B.(-3,0)????
C.(0,3)??? D.(0,-3)
B
即学即练
3、已知方程ax+b=0的解是-2,下列图像肯定不是直线y=ax+b的是( )
A
B
C
D
B
即学即练
x=2
2
解:由图象可知x+3=0的
解为x= ?3.
3
x
y
0
-3
从“形”上看
析:直线y=x+3的图象与x轴交点坐标为(-3,0 ),这说明方程χ+3=0的解是x=-3)
4、方程 的解是 ,则函数
在自变量 等于 时的函数值是8.
5、根据图象,你能直接说出一元一次方程 的解吗?
即学即练
因为任何一个以为未知数的一元一次方程都可以变形为 的形式,所以解一元一次方程相当于在某个一次函数 的函数值为0时, 求 的值.
自变量x
归纳小结
解一元一次方程ax+b=0 (a ,b为常数)可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,这相当于已知直线y=ax+b,确定它与x轴交点的横坐标的值。
即:
目标导航二
一次函数与一元一次不等式
1.直线 y=ax+b 在坐标系中的位置如图,
则方程 ax+b=0 的解是 x= ____
0
-4
3
x
y
- 4
复习巩固
2、画出一次函数 y=3x+2 的图象。
x 0
y=3x+2 2 0
复习巩固
思考:
问题1与问题2有什么关系?
问题2:
自变量为何值时,函数y=2x-4的值大于0?
问题1:解不等式2x-4>0
提出问题
知识点 一次函数与一元一次不等式
认真阅读课本第96至97页的内容,完成下面练习并体验知识点的形成过程。
自主研学
1、观察下面3个不等式有什么共同点与不同点?
(1) >2;
(2) <0;
(3) <-1
合作探究
3个不等式相同的特点是:不等号左边都是_______;不同点是:不等号及不等号右边分别是____ ,_____,_____。
2
0
-1
合作探究
你能从函数的角度对以上3个不等式 进行解释吗?
解释1:
解这3个不等式相当于在一次函数
的函数值分别为_____、_____ 、 _____时,求自变量的取值范围。
大于2
小于0
小于-1
合作探究
解释2:
在直线 上取纵坐标分别满足大于2、小于0、小于-1的点,看他们的横坐标分别满足什么条件。
当y>2时,则x>0
当y<0时,则x<
当y<-1时,则x<-1
合作探究
结论
因为任何一个以为求知数的一元一次不等式都可以变形为 ax+b>0 或 ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的值 _____或_____时,求自变量x的________。
大于0
小于0
取值范围
合作探究
-2
x
y=3x+6
y
例 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
1、已知函数 y=x-3 ,
当x____时,y>0;当 x____时,y<0。
2、已知一次函数 y=kx+b的图象如图所示,则不等式 kx+b>0的
解集是( )
A.x>-2? B.x<-2
C.x>-1???? D.x<-1
>3
<3
B
即学即练
3、利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
即学即练
4、直线 y=x-1 上的点在 x 轴上方时对应的自变量的范围是( ? )
A. x>1?? B. x≥1 C. x<1?????D. x≤1
5、已知直线 y=2x+k 与 x 轴的交点为 (-2,0),则关于x的不等式 2x+k<0 的解集是 (? )
A. x>-2????B. x≥-2 C. x<-2????D. x≤-2
A
C
即学即练
可以看出,当x<2时这条直线上的点在x轴的下方,
解法一:化简得3x-6<0,画出直线y=3x-6,
即这时y=3x-6<0,所以不等式的解集为x<2
例: 用画函数图象的方法解不等式 5x+4<2x+10
y
x
-6
2
0
Y=3x-6
合作探究
解法二:画出函数 y = 2x+10 y = 5x+4图象
从图中看出:当x <2时
直线 y = 5x +4 在 y = 2x +10的下方
即 5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10 的解集是
x < 2
Y1=5x+4
y
x
0
Y2=2X+10
2
-2
合作探究
1.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x+2的解集是______。
2.当自变量x为何值时,函数y=2x-4的值大于0?
解:由题意,得 2x-4>0
x>2
∴当自变量x>2时,函数y=2x-4的
值大于0
x≥2
即学即练
2、试根据函数y=3x-15的性质或图象,确定取何值时:
(1)y>0; (2)y<0
解:令3x-15=0,解得,x=5
∵函数y=3x-15中k=3>0,
∴y随x的增大而增大,
∴(1)当x>5时,y>0;
(2)当x<5时,y<0。
即学即练
因为任何一个以x为求知数的一元一次不等式都可以变形为____________
_______________ 的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的函数值大于0或小于0时,求自变量x的_________。
ax+b>0 或
ax+b<0(a≠0)
取值范围
归纳小结
一次函数与一元一次不等式的关系
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
目标导航三
一次函数与二元一次方程组
1.直线 y=ax+b 在坐标系中的位置如图,
则方程 ax+b>0 的解是 x ____
x
y
0
3
-4
>- 4
知识回顾
25
15
5
10
20
x
0
y
2、画出一次函数y=x+5与y=0.5x+15的图象。
解:列表,得
x 0 20
y=x+5 5 25
y=0.5x+15 15 25
描点、连线得:
y=0.5x+15
y=x+5
3.上图中两条直线的交点坐标是( , )
20
25
知识回顾
(1)把二元一次方程y-x=1
写成一次函数y=____________的形式
2、你能找出方程的几组解吗?
3、把以这几组解为坐标的点在坐标系上描出来,你发现了什么?
x+1
1、画出一次函数y=x+1的图像
4、以二元一次方程y-x=1的所有解为坐标的点都在一次函数y=x+1的图像上吗?
问题探究
探究
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y=x+1
即: 二元一次方程 (数)
相应的一次函数的图象一条直线 (形)
对应
结论:
以二元一次方程的解为坐标的点都在相应的函数图象上.反过来,
一次函数图象上的点的坐标都是相应的二元一次方程的解.
认真阅读课本第97页的内容,完成下面练习并体验知识点的形成过程。
知识点一 一次函数与二元一次方程组
自主研学
问题:
1号探测气球从海拔5米处出发,以1米/分的速度上升.与此同时 ,2号探测气球从海拔15米处出发,以0.5米/分的速度上升.两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系;
(2)在某个时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
合作探究
分析:
(1) 气球上升时间满足__________。
1号气球的函数解析式为_________;
2号气球的函数解析式为_________ 。
(2) 在某个 时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有__________。 则只需求出x和y的值。
0≤x≤60
y=x+5
y=0.5x+15
相同的y值
合作探究
解:联立方程组:
y=x+5
y=0.5x+15
解二元一次方程组得:
x=_____
y=_____
答:当气球上升 分钟时,两气球都位于海拔 米的高度.
20
25
25
20
合作探究
答:1.一般地,因为每个含有求知数和的二元一次方程组,都可以改写为_______的形式,所以每个这样的方程都对应一个一次函数,于是也对应________。这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解。
思考:
新课引入中函数图象,你能解释两直线的交点坐标(20,25)就是问题3的解吗?
y=kx+b
一条直线
合作探究
从“数”的角度看,解二元一次方程组,相当于求自变量为何值时相应的两个函数值_____,以及这个函数值是多少;
从“形”的角度看,解二元一次方程组,相当于确定________的交点坐标。因此,我们可以用画一次函数图象的方法得到方程组的解。
相等
两条直线
得出结论
1、以方程2x-y=1的解为坐标的点都在
一次函数 ______的图像上。
2、方程组 的解是 ,由此可知一
次函数 与 的图像必有一个交点,
且交点坐标是 。
x-y=4
3x-y=16
y=2x-1
x=6
y=2
y=x+4
y=-3x+16
(6,2)
即学即练
3、根据下列图象,你能说出它表示哪个方程组的解?这个解是什么?
1
1
x
y
o
y=2x-1
y=-3x+4
即学即练
4、方程组 的解是
则函数 与 的交点P的坐标是______
5、一次函数y=3x-4的图象是一条直线,它由无数个点组成的,那么方程3x-y=4 的解有( )
A.1个 B.2个 C.3个 D.无数个
D
即学即练
2x+y=4
2x-3y=12
用图象法解方程组:
①
②
解:
由①得:
由②得:
作出图象:
观察图象得:交点为(3,-2)
∴方程组的解为
x=3
y=-2
x
o
y
y=-2x+4
y=2/3x - 4
合作探究
二元一次方程组的解与以这两个方程所对应的一次函数图象的交点坐标相对应。
由此可得:
二元一次方程组的图象解法.
写函数,作图象,找交点,下结论
合作探究
y
o
x
x-y=0
2x+y=5
作出图象:
观察图象得:交点(1.7,1.7)
∴方程组的解为
x=1.7
y=1.7
精确!
图象法:
你有哪些方法?
解方程组
代数法:
x=5/3
y=5/3
∴方程组的解为
用作图象的方法可以直观地获得问题的结果,但有时却难以准确.为了获得准确的结果,我们一般用代数方法.
近似!
合作探究
y=x
y=-2x+5
例:老师为了教学,需要在家上网查资料。电信公司
提供了两种上网收费方式:
方式 1 :按上网时间以每分钟 0.1 元计费;
方式 2 :月租费 20 元,再按上网时间
以每分钟 0.05 元计费。
请同学们帮老师选择:以何种方式上网更合算?
合作探究
o
y/元
x /分
20
400
200
y1 =0.1x
y 2=0.05x+20
40
30
在同一坐标系中分别画出这两个函数的图像
当 x = 400 时,
y1 = y2
当 x>400 时,
y1 > y2
当 0≤x<400 时,
y1 < y2
y1=0.1x
y2=0.05x+20
解:设上网时间为 x 分,若按方式 1 则收 元;
若按方式 2 则收 元。
y1=0.1x
y2=0.05x+20
由函数图像得:
当 时,y>0,
即选方式 省钱;
当 时,y=0,
即选方式A、B ;
当 时,y<0,
即选方式 省钱;
400
y=-0.05x+20
20
0
y
x
解法2:设上网时间为 x 分,方式 B与方式 A两种计费的差额为
y元,则 y 随 x 变化的函数关系式为 .
化简得 。
在直角坐标系中画出这个函数的图像。
y=(0.05x+20) -0.1x
y=-0.05x +20
0≤x<400
X=400
X>400
A
B
一样
在一元一次方程一章中,我们曾考虑过下面两种移动电话计费方式:
方式一 方式二
月租费 30元/月 0
本地通话费 0.30元/分 0.40元/分
用函数方法解答如何选择计费方式更省钱
方式一费用: y1 = 0.3x + 30
方式二费用: y2 = 0.4x
两种计费差额为 : y = y1-y2 = -0.1x + 30
当 x <300 分时,y>0 ,y1>y2 ,方式二省钱
当 x = 300 分时,y =0 ,y1 =y2 , 方式一方式二一样
当 x > 300分时,y<0 ,y1<y2 ,方式一省钱
300
0
30
x
y
合作探究
方程(组)与函数之的互相联系,从函数的角度可以把它们统一起来,解决问题时,应根据具体情况灵活地把它们结合起来考虑。
归纳小结
1、当自变量取何值时,函数 与
的值相等?这个函数值是多少?
解:由已知可得:
2.5x+ 1 = 5x+ 17,
解得:x=-6.4
则这个函数值y=5×(-6.4)+17=-15
检测目标
解:由题意可得:
当直线y=3x+ 6与χ轴相交时,y=0
即3x+ 6=0, 解得:x= -2,
2、直线 与 轴的交点的横坐标的值是方程 的解,求 的值.
当x= -2 时,2 x (-2) + a =0
解得:a = 4
检测目标
下方
3.若关于x的不等式
的解集为
则一次函数
当
时,图象在
时,图象在x轴______.
x轴_________;当
上方
分析:可以画出函数草图进行解答
检测目标
4.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
x<-2
分析:即求y>-2时x的取值范围
检测目标
5、看图象解不等式
x
o
y=5x-3
2
y=3x+1
7
y
从图中看出,当x>2时,直线y=5x-3上的点在直线y=3x+1上相应点的上方,即5x-3>3x+1,所以不等式的解集为x>2。
检测目标
6、直线y=-x+4和y=2x-5直线的交点坐标是________。
7、一次函数 与 的图象是两条_____的直线,因此 的解的情况是______。
(3,1)
平行
无解
检测目标
8、考虑下面两种移动电话计费方式:
用函数方法解答何时两种计费方式费用相等。
方式一 方式二
月租费(元/月) 30 0
本地通话费
(元/分钟) 0.30 0.40
检测目标
解:设电话费用为y元,通话时间x分钟,则
方式一:
方式二:
y=30+0.3x
y=0.4x
因为函数y=30+0.3x与函数y=0.4x的图象交于点(300,120),因此当通话时间为300分钟时,两种计费方式的费用相等(都是120元)。
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
